Файловый архив студентов. Файловый архив студентов.
1306 вузов, 5172 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Пензенский Государственный Университет Архитектуры и Строительства
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

2209

.pdf
Скачиваний:
0
Добавлен:
16.06.2024
Размер:
5.71 Mб
Скачать
☆

Освобождаясь от знаков сумм и выполнив усреднения величин, формирующих факторы излучения, получим

 

 

2 c ab

 

 

 

 

 

C2m

 

 

 

 

1

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

0 0

 

 

в

 

 

 

 

 

 

 

 

 

 

 

P

 

 

V

 

 

 

 

 

 

 

 

 

 

 

 

 

(

2

 

 

 

 

 

 

 

2 fm

 

 

2H

 

m(n)

 

 

 

 

 

 

 

(n)

 

 

 

 

 

nср 0,5 nср

 

 

 

ср

 

 

 

fm1(n) cos m1(n) V(

2m)n

 

nвmср2

B2

 

1

 

 

 

 

2

 

 

2

2

 

fn (m)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ср

 

 

 

 

 

 

 

 

 

 

mср mср

 

 

 

 

 

 

 

 

 

 

 

 

 

 

fn1(m) cos n1(m) ) ,

 

 

 

где

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m m

 

 

 

 

 

 

 

 

n n

 

 

 

 

 

 

Vm2(n) вVm2(n) ; Vm2(n) вVm2(n)

 

 

 

 

 

 

m mн

 

 

 

 

 

 

 

 

n nн

 

 

 

fm2 (n) cos m2 n

fm1(n) cos n2 (m)

.

Здесь число nср относится к частоте

 

 

 

 

fmн n fmв n

с числом

 

fcp m(n)

 

mнв

 

mнmв , mн 1, а число mср – к частоте

 

 

 

 

fnн m

fnв m

с числом

 

 

fср

 

nнв nнnв , nн 1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Числа nср`2,

mср`2 отнесем к расчетным резонансам соответственно с

частотами

 

 

 

 

 

 

 

 

что

позволяет

освободиться

от

знаков сумм

 

 

 

fср ,

 

 

fср ,

 

n nB

m mB

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

;

 

 

 

 

путем введения множителей тВпВ.

 

 

 

 

 

 

 

 

 

 

 

 

n nB

m mH

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Усреднивфакторыизлученияпоширинеинтервала f

fв

fн , причем

fcp

 

fн fв

 

 

 

 

 

 

и считая,

что для n ср,

m ср угол

 

 

 

представим

 

 

 

 

 

 

 

 

 

fср

fср ,

2

 

мощность в виде

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

c

 

f

 

cos

 

 

 

 

 

 

 

 

m C2

 

 

 

 

 

 

 

nвmcp2 B2

 

 

 

 

 

 

 

 

в

в

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

0

 

 

 

 

 

 

 

 

в

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

 

 

 

 

 

ab

 

 

 

 

 

V

 

 

 

 

 

 

 

 

V

 

 

 

 

 

 

 

 

 

 

 

(3.55)

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

2

 

 

2

 

2

2н

 

 

 

 

 

 

f

 

 

m(n)

 

n

 

0.5

n

 

 

 

(m)n

m

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

cp

 

cp

 

 

 

 

 

 

cp

 

cp

 

 

 

51

Здесь в arcsin

 

в

 

arcsin

fcp

.

 

 

 

 

 

 

 

cp

 

fв

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Коэффициент звукоизлучения в этом случае

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

2

 

 

 

 

 

 

 

4 fв cos в

m

 

C2

 

n

mcp B

 

 

.

(3.56)

S

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 2

 

 

H

 

2 f

 

 

 

в

ncp

 

 

2

в

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0,5 nср

 

 

mcp mср

 

 

3.3.3. Излучение в области простых резонансов

Излучаемая мощность в условиях простых резонансов (3.24) на каждой частоте

P

0c0

V 2

abS ,

(3.57)

2m n

2

m n

m n

 

 

 

 

где коэффициент излучения

 

 

16 m

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S

 

 

sin m

Bn cos n Cn

 

C n 0.5 sin n

(3.58)

4

 

 

 

n

 

 

 

2

2

 

2

 

2

 

 

 

2

 

2

 

 

 

 

m n

 

 

 

0,5

m

 

 

 

 

cos m n

 

 

 

 

 

 

 

 

n

 

 

 

 

m

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

K0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

cos m n

 

 

 

2

 

 

 

 

 

 

 

2

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

K0

 

a

 

 

 

 

 

b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Наибольшие значения выражение (3.58) имеет при n 12 , 32 , 52 ...; m 12 , 23 , 52 ...

При возбуждении пластины диффузным звуком, излучаемая мощность равна

n nв

n nв

 

 

m mв m mв

 

 

P2n P2m n .

(3.59)

m mн

 

1

 

 

n n

m

 

2

 

 

н

 

 

1

 

 

 

 

 

 

 

 

n

2

 

 

52

Здесь Р2m n – представляет усреднённое значение мощности в интер-

вале частот f(m)(n).

Используя выражение мощности на каждой частоте (3.57), получим

 

 

 

 

 

n nв

n nв

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8 c ab m mв

 

2

 

m mв

 

 

m2C2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P2n

0 40

V(m)(n)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m

 

 

 

2

 

2

 

 

 

 

 

m mн

´

 

 

 

 

 

2

2

 

 

 

 

 

 

 

 

 

n nnн

 

 

1

n 0.5 n

 

 

 

m

 

 

 

 

 

 

 

m

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

(3.60)

 

 

 

 

 

 

 

 

 

n

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

K0 m2 n2

 

 

 

K0 m n dK0 m n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

,

 

 

 

 

 

K0 m n

 

 

 

 

 

 

 

2

 

 

 

 

 

2

 

 

 

 

 

 

 

K0 m1 n1

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

K

 

m

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0 m n

 

 

 

 

 

b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

2

– усредненное по частоте в пределах

 

f(m)(n) значение колебатель-

где V

 

 

(m)(n)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ной скорости пластины.

Проведя необходимые действия суммирования и усреднения,

 

 

 

 

 

8 c

 

 

 

 

 

 

 

 

 

 

 

mср2 C2

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

п

 

 

 

 

 

 

abV

 

 

N

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

4

 

 

 

(m)(n)

 

 

 

 

 

 

 

2

 

2

 

2 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

nср 0,5 nср

 

(mср mср)

 

 

 

 

 

 

1

 

 

f

m n в

cos

m n cp

f

m n cp

cos

m n cp

.

 

 

 

 

 

fв

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Здесь

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n nв

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V(

2m)(n) вV(

2m)(n) ;

 

 

mcp mнmв ; ncp nнnв

 

 

 

 

 

 

 

 

 

m mн

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n nnн

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

N – число резонансов в полосе

 

f.

 

 

 

 

 

 

 

 

 

 

Считая, что θ(m)(n)ср =

зависимость (3.61) запишем в виде

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

получим

(3.61)

 

 

 

 

 

 

 

0c0

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

 

 

V

 

 

abS ,

 

 

 

 

 

 

 

(3.62)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2n

 

 

2

 

(m)(n)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

где

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

16

N

 

mcp2

 

 

 

 

 

 

c2 cos

 

 

 

f

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S

 

 

 

 

 

 

 

в

в

.

(3.63)

4

 

 

 

 

 

 

 

 

 

ncp

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

2

2

 

 

 

2 f

 

 

 

 

 

 

 

mcp mср

 

 

 

0,5 nср

 

 

 

 

 

 

 

 

 

 

 

 

 

 

53

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

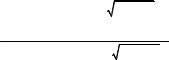
Число резонансов N найдем из зависимости [42]

N

 

2 ba

fг ,

(3.64)

f

c2

 

 

0

 

 

fг – граничная частота волнового совпадения.

3.4. Влияние внутренних потерь на изменение колебательной скорости

При колебаниях реальных конструкций часть энергии расходуется на преодоление внутреннего трения. Работа сил внутреннего трения

W

mn2

a b U 2

x, y dxdy,

(3.65)

0

2

 

 

 

 

 

 

 

 

 

0 0

 

 

где η – коэффициент потерь.

Тогда с учетом потери энергии на преодоление внутреннего трения экстремальные свойства колеблющейся пластины (3.19) представляем в виде

 

 

 

 

 

 

 

a b

 

 

a b

 

 

 

 

 

2

2

 

 

2

 

 

 

 

 

U

 

 

 

2

mn 1

U

 

x, y dxdy p x, y U (x, y)dxdy

0. (3.66)

 

 

 

i

 

 

mn

 

 

 

 

0 0

 

 

0 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Откуда при m = m', n = n'

 

 

 

 

 

 

 

 

 

 

 

 

 

Umn

 

pвmn

 

G,

(3.67)

 

 

 

 

 

 

 

 

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

mn 1

i

 

 

 

где

G

d 1 g2 e kb 1 sin2

 

2 1 g2 2e 2kb 1 sin2 .

(3.68)

Считая, что колебательная скорость связана со смещением соотношением V= iωU, определим квадрат колебательной скорости

2

 

 

 

p2

2G2

 

.

(3.69)

Vmn

 

 

в mn

 

 

 

 

2

 

2

2 2

2

 

 

 

 

mn i mn

 

 

Здесь pв mn – суммарная амплитуда звукового давления в падающей и отраженных волнах.

54

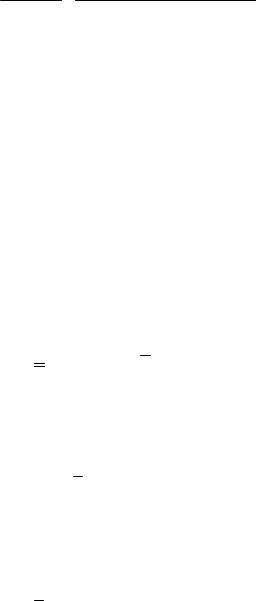
В единичном интервале частот, квадрат колебательной скорости:

 

 

2

p

 

G2

 

2d

 

 

 

 

2

,

(3.70)

Vmn

2

mn

2 2 2

 

 

 

0 mn

 

 

 

 

 

0 mn i mn

где p02mn – квадрат звукового давления в падающих волнах в заданном

интервале частот.

Рассматривая возбуждение пластины звуковыми волнами диффузного поля в интервале частот Δω, найдем выражение усредненного квадрата колебательной скорости

 

 

 

 

 

m mв

2

 

 

 

 

 

 

 

 

 

 

 

 

 

2

n nв

 

 

2

 

 

 

 

 

 

 

2

G

 

pв mn

 

 

 

d

 

 

 

.

(3.71)

V

 

 

 

 

 

2

 

 

 

 

 

 

2

 

 

 

mn m mн

 

2

2

2

 

 

 

 

 

 

 

 

n nн

 

0

mn i mn

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

После интегрирования и преобразований, получим

 

2

G2

 

p

2

 

 

 

V

2

 

в

 

,

(3.72)

2

 

 

 

 

 

mn

 

 

где mn – среднегеометрическое значение между частотами наинизшего и наивысшего резонансов в рассматриваемом интервале Δω.

pв2 p02mn N .

Квадрат звукового давления найдем как сумму квадратов давлений, падающих на пластину волн в пределах телесного угла между двумя косинусами, образующие которых имеют с нормалью к пластине углы θн и θв.

н

 

pв2 2 p2 cos sin ,

(3.73)

в

гдеp – звуковоедавлениепридиффузномпадениизвукавпределахот0 до 2 .

Далее рассмотрим процесс формирования колебательного поля в области неполных пространственных резонансов. Для случая m = m'; n ≠ n' ограничиваясь наибольшими абсолютными значениями амплитуды, получаем:

 

2 pв mn M

 

 

 

Um n

 

,

(3.74)

2

2

 

n 12

m n 1 i

 

 

 

(n 0,5 n )

 

 

 

55

 

 

 

 

где

 

M

1 g2 e kb 1 sin2

 

 

 

 

 

 

 

.

 

 

 

 

 

 

1 g2 e kb 1 sin2

 

 

 

 

 

Во втором случае, при m ≠ m , n = n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 pв m nmG

 

 

 

 

 

U m n

 

 

 

 

 

 

 

.

(3.75)

 

 

2

1 i

2

(m

2

 

2

 

1

 

 

 

 

 

 

 

n

2

 

 

 

m n

 

 

 

 

 

 

 

 

 

Здесь G по формуле (3.68).

Освобождаясь от знака сумм, находим квадрат колебательной скорости в каждом частотном интервале

 

 

2

 

 

pв2mn

 

 

2

 

 

 

 

 

2d

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

,

(3.76)

Vm(n)

 

M

 

 

 

 

 

 

 

 

 

 

 

4 2

 

 

 

 

2

 

 

2

2

2

 

 

 

 

 

 

m n

 

 

 

 

0

 

m n i m n

 

 

 

 

 

 

2

 

p 2

 

G

2

 

2

2d

 

2

 

2 .

(3.77)

 

 

 

 

 

 

 

V(m)n

4 2

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

в m n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m n

 

 

0

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m n

 

 

(m)n

 

 

 

 

Если на пластину воздействует диффузное звуковое поле в интервале частот , то с учетом зависимостей (3.76), (3.77) запишем

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p2

 

 

 

 

 

 

 

 

 

 

 

 

 

V 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

в mn

 

 

 

 

M 2 ,

(3.78)

 

 

 

 

 

 

8 2

 

 

 

 

 

 

 

 

m(n)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V

2

 

 

 

 

pв m n

 

 

 

 

 

G2 .

(3.79)

 

 

 

 

 

 

 

 

 

8 2

 

 

 

 

 

 

 

 

 

 

 

(m)n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m n

 

 

 

 

 

 

Здесь

 

2

p2 N

 

 

;

 

 

2

 

 

 

p2 N

 

 

 

 

;

 

 

p

m n

 

p

 

 

 

m n

 

 

 

в mn

mn

 

 

 

 

в m n

m n

 

 

 

 

или

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

н

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

н

 

 

 

 

 

в2mn 2 p1

cos sin ; pв2m n

2P2 cos sin

 

 

 

 

p

 

 

 

 

 

в

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

в

 

p1 p2 p

56

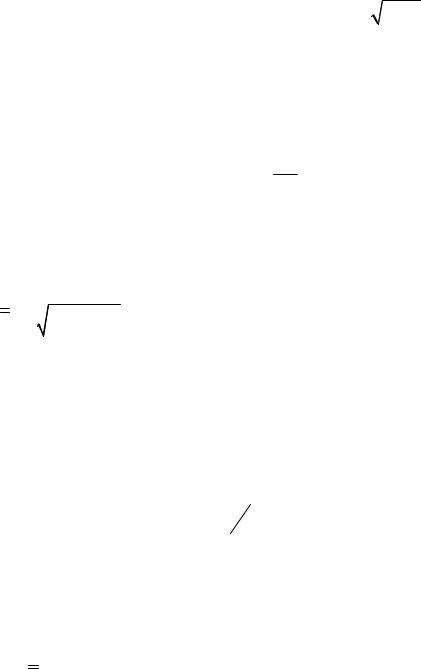
Тогда, считая

н

 

,

что соответствует

частоте

 

fср

fн fв можно

найти

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

2

 

 

 

fср

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

pв m n p1 1 sin

в p2

 

 

 

 

,

(3.80)

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

fв

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

pв2m n p1 1 sin2 в p1 1 ffсрв 2 .

В итоге усредненное значение квадрата колебательной скорости неполного пространственного резонанса

 

 

 

 

 

 

 

 

 

 

 

fср

2

 

2

 

 

 

 

 

2

 

 

 

2

 

2

 

 

 

 

p GM

 

 

 

 

 

 

 

 

 

 

 

V

 

Vm(n)Vn(m)

8

1

 

 

 

 

 

 

 

 

.

(3.81)

f

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

в

 

 

mn ср

 

 

 

Аналогично предыдущему, определим влияние внутренних потерь на квадрат колебательной скорости в области простых резонансов. Амплитуда колебаний в этом случае

 

4 pв m n m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U m n

Bn cos n m (n)

Cn

Cnsin n m (n) sin m m (n)

M

(3.82)

 

2

 

 

 

2

 

2

 

1

 

 

2

 

2 2

 

2

 

n 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

w m

(n) 1 i w

 

 

n

 

 

 

 

m

 

 

 

 

m 0

 

 

 

2

 

n

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Усредняя звуковое давление в интервале Δω, относя полученные средние значения к среднегеометрическому резонансу и суммируя энергию в падающих звуковых волнах, находим

 

 

 

 

 

 

 

fср

2

 

p

2

 

 

 

 

 

 

2

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

V

 

 

1

 

 

 

 

 

 

 

 

 

M

 

.

(3.83)

32

f

 

 

 

2

 

 

 

 

 

 

 

 

 

в

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m n ср

 

 

 

 

 

Полученные зависимости (3.72), (3.81) и (3.83) показывают, что квадрат колебательной скорости пластины обратно пропорционален коэффициенту потерь, т.е. с увеличением внутренних потерь колебательная скорость снижается практически во всей расчетной области частот.

57

3.5. Определение расчетных формул звукоизоляции

Собственную звукоизоляцию пластины будем искать, исходя из представления о суммарной акустической мощности в верхней среде [30]

R 10lg

P1

,

(3.84)

P

 

 

 

 

2

 

 

где Р1 – суммарная звуковая мощность в верхней среде; Р2 – прошедшая мощность.

Суммарную звуковую мощность Р1 в среде перед ограждением представим в виде

 

 

P P'

P" ,

 

 

 

 

1

1

 

1

 

 

 

 

здесь P1 ,

P2 – соответственно падающая и

отраженнаяP2

мощности.

Причем

 

 

 

 

 

 

 

 

 

 

 

 

P

 

abp2

.

 

(3.85)

 

 

 

 

 

 

 

 

1

 

8 c

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

0

 

 

 

Считая P'

P'' , можем записать

 

 

 

 

 

 

 

 

 

1

1

 

 

 

 

 

 

 

 

 

 

P

 

abp2

 

,

 

 

(3.86)

 

 

4 0c0

 

 

 

 

1

 

 

 

 

где p – суммарное амплитудное звуковое давление в верхней среде. Акустическая мощность (3.45), излучаемая пластиной, в области

полных пространственных резонансов, с учетом найденного значения квадрата колебательной скорости (3.72)

 

2

c

 

 

p

2

 

 

 

 

 

 

 

 

 

 

 

P G

ab

 

 

 

S .

 

 

0 0

 

в

 

(3.87)

 

2

 

2

 

4

 

 

 

 

 

 

 

 

 

mn

 

 

 

 

 

Используя выражения квадрата звукового давления (3.73), суммарной и прошедшей звуковых мощностей (3.86), (3.87), получим

2

 

 

 

2

mn

G 2

 

R 10lg

 

 

 

 

 

 

.

(3.88)

0c0 0c0

 

 

 

cos2 в cos2 н

 

 

 

S

58

Считая, 0c0

0с 415 кг м2с ,

2 f , выражение собственной

звукоизоляции запишем в виде

1,46

 

 

2 fmn f G 2

 

R 10lg 104

 

 

 

.

(3.89)

 

 

cos2 в cos2

 

 

S

Здесь – масса единицы площади ограждения;

 

fmn – среднегеометрическая частота расчетного

интервала

f f1 f2 , Гц;

S – усредненная характеристика звукоизлучения, определяемая по формуле (3.46).

Углы в , θн соответствуют частотам f1, f2 и определяются

arcsin c0 cu .

Здесь с0 344 м/с;

сu – скорость распространения изгибных волн в пластине.

Поскольку sin2

f

, cos2

 

cos2 2 f

 

f

 

выражение (3.89)

f

 

 

 

f f

 

 

с

 

 

2

 

1

 

2

2

 

принимает вид:

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R 10lg

0,7 G 2 2 f 3

,

 

(3.90)

 

 

 

104

f2mnS

 

 

 

 

 

 

 

 

 

 

fгmn fг граничная частота полных пространственных резонансов.

Аналогичнымобразомопределимзвукоизоляциювобластичастотниже

граничной fгmn .

В условиях неполных пространственных резонансов излучаемая мощность определяется выражением (3.55).

Тогда с учетом соотношений (3.84) и (З.86) для анализа звукоизоляции в третьоктавных полосах fв cos в / f 2,3 имеем

R 10lg

7,3 2 f f

 

,

(3.91)

 

 

 

 

104 S G M

 

 

 

 

 

где S , М, G – находятся соответственно по формулам (3.56), (3.74), (3.68).

59

В случае

 

анализа

 

прохождения

звука

в

октавных полосах:

fв cos в / f

0,2

 

собственная

 

звукоизоляция

будет

определяться

выражением

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R 10lg

3,3 2 f f

 

.

 

 

 

 

 

(3.92)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

104 S G M

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В условиях простых пространственных резонансов излучаемая

акустическая мощность

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

c

 

 

 

 

 

p2

 

M 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

abN

 

 

S

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0 0

 

( f , )

 

 

 

 

 

.

 

 

 

(3.93)

 

 

 

 

 

 

 

 

 

8

2

 

 

 

 

 

 

 

 

 

 

2

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

mn

 

 

 

 

 

 

Тогда звукоизоляция

в

области

частот

fг m n f

fгm(n)

будет

определяться как

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(3.94)

R 10lg

1,4 2 f f

 

– для третьоктавных полос;

 

 

 

 

 

103

 

 

 

 

 

 

 

 

 

 

 

 

S2M 2

 

 

 

 

 

 

R 10lg

6,04

f f

– для октавных полос.

 

 

 

 

 

 

 

 

(3.95)

104

 

 

 

 

M 2

 

 

 

 

 

 

 

 

 

 

 

S

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Усредненная

характеристика

звукоизлучения

 

 

в

этом

случае

 

 

S

определяется в соответствии с зависимостью (3.63).

 

 

 

 

 

На основе анализа состояния волновых полей установлено, что деление частотной характеристики звукоизоляции однородной прямоугольной пластины на три характерные области частот: простых, неполных и полных пространственных резонансов является правомерным и для пластин, подкрепленных ребрами жесткости. В условиях простых и неполных пространственных резонансов при совпадении круговой текущей частоты с круговой частотой собственных колебаний пластины звук проходит полностью, если не учитывать потери энергии на внутреннее трение и сопротивление излучению.

Увеличение размеров и внутренних потерь ограждения приводит к повышению звукоизоляции в области неполных пространственных резонансов.

Звукоизоляция ограждающих конструкций с ребрами жесткости определяется массой ограждения, частотой звука, коэффициентом потерь, размерами ячеек, заключенных между ребрами жесткости.

60

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности