
2209
.pdf
Граничные условия на левом конце балки:
2UI |
|
0 |
(2.20) |
||
|
x2 |
x 0 |
|||
|
|
||||
UI x 0 0 .
|
|
|
|
|
|
|
kx K4 kx 0. |
||||||||||
При x=0 K1 kx I , a K2 k x |
K3 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С учетом (2.20), выражение U x для первого участка принимает вид: |
|||||||||||||||||
|
UI C2K2 kx C4K4 kx . |
(2.21) |
|||||||||||||||
В сечении x l1 |
значения функции U x |
должны удовлетворять усло- |
|||||||||||||||
виям сопряжения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UI x l |
|
UII |
x l |
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
||
|
|
|
U |
|
|
|
|
U |
|
|
|
|
|||||
|
|
|
|
x |
I |
|
|
|
|
|
II |
|
|
||||
|
|
|
|
|
x l |
|
|
|
x x l |
|
|
||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
||
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
(2.22) |
|||
|
|
|
UI |
|
|
|
UII |
||||||||||
|
|
|
x2 |
|
x l |
|
|
|
x2 |
|
x l |
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
||||
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
R |
|
|
|
|
UI |
|
|
|
|
|
UII |
|
|
|
|
|
||||
|
|
|
x3 |
|
|
EJ |
|||||||||||
|
|
x3 |
x l |
|
|
x l |
|||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
Все эти условия удовлетворятся, если принять при общем для обоих пролетов начале отсчета, что
U |
II |
U |
I |
|
R |
K |
4 |
k x l |
. |
(2.23) |
|
|
|||||||||||
|
|
|
EJk3 |
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
Выполнение условий (2.22) легко проверить, воспользовавшись правилами дифференцирования функций Крылова и учитывая, что
K1 0 I, a |
K2 0 K3 0 K4 0 0. |
Считаем, что в сечении x l1 приложена опорная реакция. Тогда в соответствии с формулой (2.23) и с учетом (2.21) для второго участка имеем
UII C4K4 kx C2K2 kx HK4 k x l1 ,
где H EJkR 3 , причем R – амплитудное значение реакции.
31

Для определения трех констант С2, C4 и H имеются три граничных условия – смещение и момент на правой опоре равны нулю, смещение в сечении х = l1, равно R/с, где с – жесткость упругой опоры.
Таким образом, получаем систему трех уравнений с тремя неизвестными:
|
|
|
|
|
|
|
|
|
|
C |
K |
2 |
kl C |
K |
4 |
kl |
|
R |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
4 |
|
|
1 |
|
|
|
|
c |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
C |
K |
|
k l l |
|
|
C |
K |
2 |
k |
l l |
2 |
HK |
2 |
kl |
0 |
(2.24) |
||||||||||||||||||
|
|
|
|
|
2 |
|
4 |
1 |
2 |
|
|
|
|
4 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
C |
K |
|
k l l |
2 |
C |
K |
4 |
k |
l l |
HK |
4 |
kl |
0 |
|
||||||||||||||||||||
|
|
|
|
|
2 |
|
2 |
1 |
|
|
|
|
|
4 |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|||||||
Для определения частот собственных колебаний определитель полу- |
||||||||||||||||||||||||||||||||||||||
ченной системы уравнений (2.24) приравняем нулю: |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
K2 kl1 |
|
|
|
|
|
K4 kl1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
K |
4 |
k |
l l |
|
K |
2 |
|
k |
l l |
2 |
|
|
|
|
K |
2 |
kl |
|
|
|
0 |
|
|||||||||||||||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||
|
K |
2 |
k l |
l |
|
K |
4 |
k |
l |
l |
2 |
|
|
|
|
K |
4 |
kl |
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Здесь |
|
c |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
k3EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Откуда находим частотное уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ctgkl1 |
cthkl1 |
ctgkl2 |
cthkl2 |
|
|
|
(2.25) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 cthkl1 cthkl2 ctgkl1 |
ctgkl2 . |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Выражение (2.25) идентично полученному ранее (2.19), что позволяет судить о возможности использования представления волнового переноса энергии с ее минимальной затратой, предложенного профессором М.С. Седовым [28], для решения задачи о собственных колебаниях подкрепленных структур.
2.4. Влияние жесткости упругих опор на волновые свойства подкрепленных структур
Проследим влияние жесткости промежуточной опоры на значения собственных чисел и характер нормальных смещений на примере двухпролетной полосы с шарнирно-опертыми краями.
32

Рис. 2.3
33
Уравнение (2.19) при с=∞ (нет смещений на промежуточной опоре) переходит в известное частотное уравнение
сtgkl1 cthkl1 ctgkl2 cthkl2
для двухпролетной шарнирно-опертой балки, полученное путем использования решения дифференциального уравнения с постоянным интегрирования [34].
При с=0 (промежуточная опора отсутствует) уравнение (2.19) принимает вид:
sin kl 0 . |
(2.26) |
Выражение (2.26) является частотным уравнением для однопролетной балки шарнирно-опертой по концам [25].
Дляпромежуточныхзначенийжесткостиупругойопорынайденыкорни частотных уравнений и получены собственные формы колебаний при l1 = l2
(рис. 2.3, табл. 2.1, 2.2).
Анализ полученных результатов показывает, что найденные собственные функции (2.17) справедливы для всех значений жесткости промежуточныхопор. Приуменьшениижесткостинаблюдаетсяувеличение отклонения полосы от положения равновесия и формы собственных колебаний становятся все более близкими к формам однопролетной полосы с шарнирно-опертыми краями. По мере увеличения жесткости опоры формы колебаний переходят в формы колебаний двухпролетной неразрезной шарнирно-опертой полосы. К тому же, для симметричных форм колебаний на промежуточной опоре фаза движения синусоидальной
волны наиболее близка к значению |
|
2m 1 |
|
, m = 1, 2, …, что характерно |
|
2 |
|
||
|
|
|
|
для жесткого защемления (рис.2.3).
Сравнение значений собственных чисел, полученных на основе представления волнового переноса энергии с ее минимальной затратой, с методикой известного решения, указывает на правильность выбранного подхода к решению задачи о собственных колебаниях подкрепленных структур.
Найденные функции суммарных смещений для двухпролетной полосы с упругой промежуточной опорой позволяют определить смещение точек полосы на любой частоте собственных колебаний. Решение может быть продолжено аналогичным образом и для случая большего количества пролетов.
Полученное решение дает возможность оценить влияние жесткости опор на характер нормальных смещений и фазовые соотношения на промежуточной опоре.
34

|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl = 3.1415 |
|
kl = 3.9164 |
|
kl = 6.2831 |
|
kl = 7.0070 |
|
kl = 9.4247 |
|
|||||
|
|
|
UI |
|
|
|
|
|
|
|
|
|
|
|
UI |
|
UII |
|
UII |
UI |
|
UII |
UI |
|
UII |
UI |
|
UII |
|
|
|
|
0.000 |
|
|
|
|
|
|
|
|
|
|
|
0.000 |
|
0.000 |
|
0.014 |
0.000 |
|
0.000 |
0.000 |
|
0.086 |
0.000 |
|
0.000 |
|
0.309 |
|
-0.309 |
0.393 |
|
0.108 |
0.588 |
|
0.588 |
0.644 |
|
-0.347 |
0.809 |
|
-0.809 |
0.588 |
|
-0.588 |
0.730 |
|
0.334 |
0.951 |
|
0.951 |
0.983 |
|
-0.809 |
0.951 |
|
-0.951 |
0.809 |
|
-0.809 |
0.964 |
|
0.609 |
0.951 |
|
0.951 |
0.857 |
|
-1.071 |
0.309 |
|
-0.309 |
0.951 |
|
-0.951 |
1.065 |
|
0.860 |
0.588 |
|
0.588 |
0.321 |
|
-0.919 |
-0.588 |
|
0.588 |
1.000 |
|
-1.000 |
1.025 |
|
1.025 |
0.000 |
|
0.000 |
-0.377 |
|
-0.377 |
-1.000 |
|
1.000 |
0.951 |
|
-0.951 |
0.860 |
|
1.065 |
-0.588 |
|
-0.588 |
-0.920 |
|
0.319 |
-0.588 |
|
0.588 |
0.809 |
|
-0.809 |
0.609 |
|
0.964 |
-0.951 |
|
-0.951 |
-0.173 |
|
0.855 |
0.309 |
|
-0.309 |
0.588 |
|
-0.588 |
0.334 |
|
0.730 |
-0.951 |
|
-0.951 |
-0.811 |
|
0.981 |
0.951 |
|
-0.951 |
0.309 |
|
-0.309 |
0.108 |
|
0.393 |
-0.588 |
|
-0.588 |
-0.348 |
|
0.643 |
0.809 |
|
-0.809 |
0.000 |
|
0.000 |
0.014 |
|
0.000 |
0.000 |
|
0.000 |
-0.086 |
|
0.000 |
0.000 |
|
0.000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
35

Таблица 2.2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ = ∞ |
γ = 12000 |
γ = 1600 |
γ = 400 |
γ = 100 |
γ = 50 |
γ = 0 |
|||||||
UI |
UII |
UI |
UII |
UI |
UII |
UI |
UII |
UI |
UII |
UI |
UII |
UI |
UII |
0.000 |
0.000 |
0.000 |
0.014 |
0.000 |
0.102 |
0.000 |
0.422 |
0.000 |
1.103 |
0.000 |
1.340 |
0.000 |
1.000 |
0.395 |
0.103 |
0.393 |
0.108 |
0.388 |
0.194 |
0.372 |
0.469 |
0.328 |
1.134 |
0.296 |
1.349 |
0.156 |
0.988 |
0.731 |
0.322 |
0.730 |
0.334 |
0.723 |
0.409 |
0.700 |
0.668 |
0.631 |
1.196 |
0.576 |
1.358 |
0.309 |
0.951 |
0.969 |
0.599 |
0.964 |
0.609 |
0.961 |
0.668 |
0.947 |
0.866 |
0.888 |
1.248 |
0.826 |
1.345 |
0.454 |
0.891 |
1.060 |
0.853 |
1.065 |
0.859 |
1.071 |
0.899 |
1.088 |
1.029 |
1.083 |
1.258 |
1.032 |
1.292 |
0.588 |
0.809 |
1.014 |
1.014 |
1.025 |
1.025 |
1.046 |
1.046 |
1.112 |
1.112 |
1.206 |
1.206 |
1.188 |
1.188 |
0.707 |
0.707 |
0.853 |
1.060 |
0.859 |
1.065 |
0.899 |
1.072 |
1.029 |
1.088 |
1.257 |
1.083 |
1.292 |
1.032 |
0.809 |
0.588 |
0.599 |
0.969 |
0.609 |
0.964 |
0.688 |
0.961 |
0.866 |
0.947 |
1.247 |
0.888 |
1.345 |
0.826 |
0.891 |
0.454 |
0.322 |
0.731 |
0.334 |
0.730 |
0.409 |
0.723 |
0.668 |
0.700 |
1.196 |
0.631 |
1.358 |
0.576 |
0.951 |
0.309 |
0.103 |
0.395 |
0.108 |
0.393 |
0.194 |
0.388 |
0.496 |
0.372 |
1.134 |
0.328 |
1.349 |
0.296 |
0.988 |
0.156 |
0.000 |
0.000 |
0.014 |
0.000 |
0.102 |
0.000 |
0.422 |
0.000 |
1.103 |
0.000 |
1.340 |
0.000 |
1.000 |
0.000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36
3.ПРОХОЖДЕНИЕ ЗВУКА ЧЕРЕЗ ОГРАЖДЕНИЯ, ПОДКРЕПЛЕННЫЕ РЕБРАМИ ЖЕСТКОСТИ
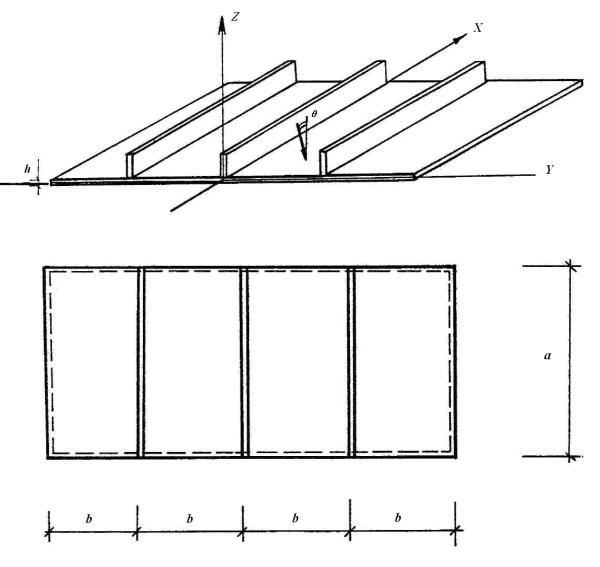
Рассмотрим прохождение звуковых волн через ограждения, подкрепленныеребрамижесткостиодногонаправления. Вкачествематематической модели ограждения принимаем конструкцию в виде прямоугольной пластины, шарнирно-опертой по краям; соединение ребер и пластины жесткое (например, непрерывный сварной шов).
В основу рассмотрения прохождения звука положим анализ состояния волновых полей, возможность их согласования [28] . Дифракционными эффектами на ребрах жесткости будем пренебрегать.
3.1. Звуковое поле в плоскости пластины
Пусть на прямоугольную пластину падает под углом θ звуковая волна. Выберем систему координат так, чтобы плоскость ХОУ совпадала со срединной плоскостью пластины, оси ОХ и ОУ были направлены из левого нижнего угла одной ячейки вдоль сторон а и b, ось OZ перпендикулярна ХОУ (рис. 3.1). Звуковое поле здесь и в дальнейшем будем характеризовать величиной звукового давления.
Предположим, что след падающей, отраженной и прошедшей волн, распространяющихся в сторону отрицательных X, У составляет с нормалью к стороне а угол α0. Итоговое звуковое давление, согласно принципу суперпозиции:
i t k |
xsin |
ycos |
|
|
, |
(3.1) |
||
p1 p0e |
0 |
|
0 |
0 |
1 |
|
||
где k0 k0 sin ; |
|
|
|
|
|
|
|
|
1 – начальный фазовый ход; |
|
|
|
|
|
|
|
|
p0 pп pom pnp ; pn , pom , pnp |
– |
амплитуды соответственно |
пада- |
|||||
ющей, отраженной и прошедшей волн.
37
Падающая в противоположном направлении волна, вместе с отраженной и прошедшей волнами, образуют на поверхности пластины след с формами распределения давления
|
|
|
xsin 0 y cos 0 |
|
|
p2 |
i t k0 |
|
2 |
(3.2) |
|
p0e |
|
|
. |
Рис. 3.1
Под другим возможным углом α0 могут распространяться в прямом и обратном направлениях падающие, отраженные и прошедшие волны, давление в которых
p3 |
i t k |
xsin |
y cos |
|
|
, |
|
||
p0e |
0 |
|
0 |
0 |
3 |
(3.3) |
|||
p4 |
i t k |
|
xsin |
ycos |
|
|
|
||
|
|
||||||||
p0e |
|
0 |
0 |
0 |
4 |
. |
|
||
38
Рассматривая действительную часть комплексных выражений (3.1), (3.2), (3.3) и считая 1 2 , 3 4 0 , получим
p1 |
p0 cos k0 xsin 0 |
y cos 0 cos wt, |
|
p2 |
p0 cosk0 xsin 0 |
y cos 0 cos wt, |
|
p3 |
p0 cosk0 xsin 0 |
y cos 0 cos wt, |
|
p4 |
p0 cosk0 xsin 0 |
y cos 0 cos wt, |
|
суммируя давление в каждой точке, имеем
p 4 p0 sin k0 xsin sin 0 sin k0 ysin cos 0 cos wt .
(3.4)
(3.5)
Принимая начальныефазовыеуглыравнымимеждусобой, получимтем же путем другое возможное значение суммарного звукового давления:
p 4 p0 cos k0 xsin sin 0 cos k0 ysin cos 0 cos wt . |
(3.6) |
Для точек х = а, у = b, можно записать
k0asin sin 0 m ; |
k0bsin cos 0 n , |
(3.7) |
где величины m , n имеют непрерывные численные значения до тех пор,
пока не будут учтены граничные условия в плоскостях XZ, YZ. Зависимости (3.5), (3.6) с учетом (3.7) можно переписать в виде
|
|
|
|
|
|
|
|
|
|
m x |
|
|
n y |
|
|
|
|||
pm n pm n sin |
|
|
|
sin |
|
|
cos t, |
|
|
|
a |
|
b |
(3.8) |
|||||
|
|
|
|
|
|
|
|||
|
|
m x |
|
|
n y |
|
|||
pm n p0m n cos |
cos |
cos t . |
|
||||||
|
|
|
|||||||
|
|
a |
|
|
|
b |
|
|
|
Здесь p0m n 4 p0 .
В случае воздействия на пластину плоских волн диффузного звукового поля результирующее звуковое давление представится в виде бесконечного двойного ряда
|
|
|
|
|
|
|
p p0m n sin |
m x |
sin |
n y |
. |
(3.9) |
|
a |
|
|||||
|
|
|
b |
|
||
m 0n 0 |
|
|
|
|
|
|
39

3.2. Распределение смещений в подкрепленной пластине под воздействием звуковых волн
Под воздействием звуковых волн в пластине возникают и распространяются свободные упругие волны, формирующие нормальные колебания. Смещение каждой точки пластины в любой момент времени представим в виде [29]
U x, y,t 2U0 XY cos t . |
(3.10) |
Здесь X sin kxsin ;
Y2dg 1 e kb 1 sin2 sin ky cos d2 1 g2 e kb 1 sin2
cos ky cos d1 2 q e kb 1 sin2 e kb 1 sin2 ek y b 1 sin2 ,
где
|
|
|
2 |
|
|
|
|
|
kb |
1 sin2 |
|
|
||
|
|
|
g sin kbcos cos kbcos e |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
2 sin |
kbcos g cos kbcos e |
kb |
1 sin2 |
qe |
2kb |
1 sin2 |
|||||||
|
d |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
g |
|
1 sin2 |
; |
d g2 1 ; |
q g2 1. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
Согласно принципу Остроградского – Гамильтона для движущихся упругих систем при наличии возмущающей силы можно записать
t2 |
k |
n |
dt |
t2 |
|
|
|||
|
E |
V |
p |
|
t |
|
|
|
t |
1 |
|
|
|
1 |
x, y,t |
|
|
|
(3.11) |
|
||||
|
U t |
0 , |
где Ек – кинетическая энергия; Vп – потенциальная энергия;
р(х,у,t) дu – виртуальная работа возмущающих сил.
Уравнение (3.11) в условиях нормальных колебаний выражает экстремальные свойства пластины. В этом случае кинетическая энергия
|
a b |
|
U x, y,t 2 |
|
|||||
Ek |
|
0 |
0 |
|
|
|
dxdy . |
(3.12) |
|
2 |
dt |
||||||||
|
|
|
|
|
|||||
40
