
2209
.pdf
полных пространственных резонансов. Каждаяиз этих областей ограничена некоторыми значениями граничных частот. Такими частотами являются:
-граничный простой пространственный резонанс;
-граничный неполный пространственный резонанс;
-граничный полный пространственный резонанс. Определим их количественные зависимости и значения.
Для области простых пространственных резонансов справедливы
условия согласования волновых полей, описываемых соотношением (3.24). Резонансные частоты, на которых выполняются условия максимального прохождения звука можно найти, рассматривая картину распределения линий равных фаз звуковых волн в плоскости пластины (рис.5.1).
Длина звуковой волны
0 2ma sin m n sin m n .
Здесь угол αmn определяется
m n m n , 2
m n arctg bman .
(5.1)
(5.2)
(5.3)
Рис.5.1. Определение частоты простого пространственного резонанса
(n =3/ 2, m = 3/2, n, m–1, 2, ... )
111

Тогда искомая частота будет равна |
|
|
|
|
|
|
||||||
|
f m (n) |
|
|
|
c0m |
|
|
. |
|
(5.4) |
||
|
2asin m n |
sin |
|
|
|
|||||||
|
|
m n |
|
|
||||||||
В первом приближении, если считать а > b, θm n = |
|
, m =1/2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
fг m (n) |
|
|
c0 |
|
|
. |
|
|
(5.5) |
||
|
4asin m n |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||
При α → |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
fг m (n) |
c0 |
. |
|
|
|
|
|
(5.6) |
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
4a |
|
|
|
|
|
|
|
Частоты неполных пространственных резонансов определим, анализируя рис.5.2.
Рис.5.2. Определение частоты неполного пространственного резонанса
(m = 1, m = 1, n = ½, n – 1, 2, ...)
112
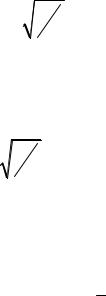
Длина звуковой волны в этом случае |
|
|
|
|||||||||
|
|
0 |
|
2a |
sin |
|
sin |
, |
(5.7) |
|||
|
|
|
||||||||||
|
|
|
m |
|
|
mn |
mn |
|
||||
|
|
|
|
|
|
|
|
|
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mn |
, |
|
arctg an |
|
|||||
|
mn |
2 |
|
|
|
|
mn' |
bm . |
(5.8) |
|||
|
|
|
|
|
|
|
|
|
||||
Тогда приближенное значение частоты неполного пространственного резонанса будет равно
fгm(n) |
|
c0m |
|
|
. |
(5.9) |
|
|
|
|
|||
|
2asin mn sin mn |
|
||||
При θmn` = π/2, m = m = 1 зависимость (5.9) примет вид |
|
|||||
fг(n)m |
c0 |
|
, |
|
(5.10) |
|
2asin |
|
|
||||
|
|
mn |
|
|||
здесь αmn определяется по формуле (5.8).
В случае полного согласования волновых полей (3.22), частота полного
пространственного резонанса |
|
|
|
|
|||
f |
|
|
c02 |
|
. |
(5.11) |
|
cmn |
2 sin2 mn |
D |
|||||
|
|
|
|
||||
В частном случае θmn = 2 ,
f |
гmn |
|
c02 |
|
D |
. |
(5.12) |
2 |
|
||||||
|
|
|
|
|
5.2.2. Подсчет усредненных характеристик звукоизлучения
Усредненные характеристики звукоизлучения S ограждений с ребрами жесткости будем определять в зависимости от способа соединения ребер с пластиной (см. разд. 5.6):
-по методике, предложенной в гл. 3, для ограждений первого типа;
-по результатам работы [28] для ограждений второго и третьего типов.
113

Расчет будем вести в 1/3 октавных полосах для трех характерных частотных областей.
1. Область простых пространственных резонансов (ПР).
Усредненная характеристика звукоизлучения ограждений с ребрами при непрерывном соединении определится как
|
|
|
36,8 |
|
1 |
|
|
|
mср2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
S |
N |
|
|
|
|
, |
||||||
|
4 |
|
2 |
2 |
2 |
2 |
||||||
|
|
|
|
|
(nср nср) |
|
|
(mср mср) |
|
|
||
где N – число резонансов по формуле (3.64).
При точечном соединении ребер жесткости
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
m2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
S 0,379 N |
|
|
ср ср |
|
|
|
|
|
|
, |
|
|
|||||||||||||
|
|
|
|
|
|
|
2 |
2 |
2 |
|
2 |
|
2 |
|
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(nср nср) |
|
(mср mср) |
|
|
|
|
|
||||||||
где m |
n |
|
|
|
abk |
|
|
|
, |
|
k |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
a2 b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ср |
|
ср |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 fasin mn sin mn |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
mср |
|
|
|
|
c0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 fbcos m n sin m n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
nср |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. Область неполных пространственных резонансов (НПР) |
|||||||||||||||||||||||||||||||
Для ограждений первого типа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
9,2 |
m |
|
|
|
|
1 |
|
|
|
|
n |
|
|
|
|
|
mср |
|
. |
|||||
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 2 |
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
в |
|
n |
|
|
0,5 n |
|
|
в |
m |
|
m |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ср |
|
|
ср |
|
|
|
|
ср |
ср |
|
|||||||
Для ограждений второго и третьего типов
N 2
S 0,933Nв ср ;
N 2 N 2
ср ср
(5.13)
(5.14)
(5.15)
114
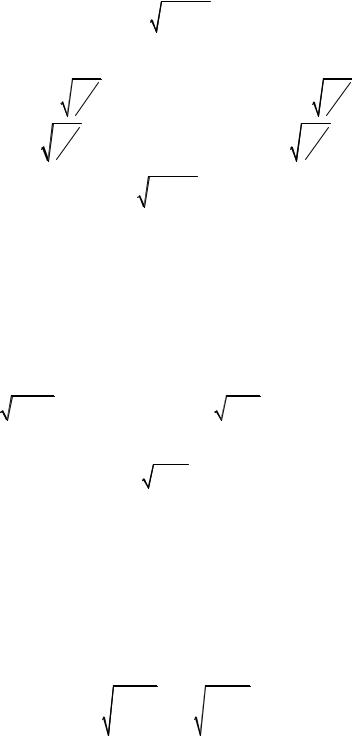
|
|
|
|
N |
в |
m n ; |
m |
|
2afв |
; n |
2bfв |
; |
|
|
|
|
|||||||||||||||
|
|
|
|
с |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
в |
в |
|
|
в |
|
|
|
|
в |
|
|
|
с |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
N |
2 |
|
|
m2 n2 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
(5.16) |
|||
|
|
|
|
|
|
|
|
|
|
|
ср |
|
|
ср |
ср |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fср |
n |
|
D |
|
|
|
|
|
|
|
|
|
|
|
fср |
m |
D |
||||||||||||
2 |
|
2bв2 |
|
|
|
|
|
2 |
|
|
|
|
|
2a2в |
|||||||||||||||||
mср |
|
|
|
|
|
|
|
|
; |
|
|
|
nср |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
D |
|
||||||||||||||
|
|
|
|
2a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2b2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nср |
nсрmср |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
tg mn bmнв |
|
|
|
|
|
|
|
tg m nanнв |
|
|
|
|
|||||||||||||
|
|
|
nср |
|
|
|
|
|
; |
|
|
mср |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
mn |
|
|
mn ; |
|
|
m n |
|
|
|
m n ; |
|
|
|
|
||||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
arcsin c0mнв ; |
|
|
|
|
arcsin |
c0nнв |
; |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
mn |
|
|
|
|
2afср |
|
|
|
m n |
|
|
|
|
|
|
|
|
2bfср |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
mнв mнmв , |
mн 1 ; |
|
nнв nнnв , |
|
nн 1 ; |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
fср |
fв fн . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При этом необходимо считать, что b=b – при малом шаге точек крепления (≤100 мм), b = kb – при большом шаге точек крепления (>100 мм), здесь k – количество ячеек.
3. Область полных пространственных резонансов (ППР) Усредненные характеристики звукоизлучения в этом случае под-
считываются по формуле
|
|
|
1 |
|
|
f |
г |
|
|
f |
г |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
S |
|
fв |
1 |
|
fн |
1 |
|
. |
(5.17) |
||||
|
|
|
|
|
|||||||||
|
|
|
f |
|
fв |
|
fн |
|
|||||
5.2.3.Построение частотной характеристики звукоизоляции
Взависимости от способа соединения ребер жесткости с ограждением формулы звукоизоляции имеют вид:
115

- для ограждений с ребрами жесткости при непрерывном соединении
R 10lg |
0.14 |
2 fср f |
(ПР) |
; |
(5.18) |
||||||||||
102 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
SM 2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
R 10lg |
7,3 |
|
2 fср f |
|
HПР ; |
(5.19) |
|||||||||
103 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
SGM 2 |
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||
R 10lg |
|
0.7 |
|
2 f 3ср |
|
ППР ; |
|
(5.20) |
|||||||
104 |
|
|
|
|
гG2 |
|
|||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
Sf |
|
|
|
|
|||||||
- для ограждений с ребрами жесткости при точечном соединении
R 10lg |
6,85 |
|
2 fср |
f |
ПР ; |
(5.21) |
|||||||
103 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
R 10lg |
1.46 |
2 fср f |
НПР ; |
(5.22) |
|||||||||
103 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
S |
|
|
|
|
|
|
|||
R 10lg |
0.73 |
|
2 f 3ср |
ППР . |
(5.23) |
||||||||
104 |
|
|
|
|
г |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
Sf |
|
|
|
|
|
|
||||
Определяя значение звукоизоляции на каждой среднегеометрической частоте по приведенным выше формулам, строим частотную характеристику звукоизоляции.
5.3. Расчет звукоизоляции ограждений
с ребрами жесткости с помощью ЭВМ
Расчет изоляции воздушного шума ограждающими конструкциями осложняется большим объемом однообразных механических вычислений. Повышение эффективности вычислительного процесса может быть достигнуто за счет использования электронно-вычислительных машин.
Алгоритм расчета звукоизоляции панелей с ребрами жесткости представим в виде блок-схемы (рис. 5.3). Изображение алгоритма в виде блок-схемы является этапом формализации задачи расчета звукоизоляции, непосредственно предшествующим разработке программы для ЭВМ. При разработке блок-схемы определяется набор исходных данных, последовательность действий, ветвления вычислительного процесса.
116

Рис. 5.3. Блок-схема алгоритма расчета
117

Элемент 2 блок-схемы задает массив стандартных среднегеометрических третьоктавных (октавных) частот анализа в диапазоне 100–10000 Гц, для которых выполняется расчет звукоизоляции ограждающих конструкций.
Блок 3 соответствует вводу исходных данных, необходимых для выполнения расчета: размеров ограждения в плане a и b, его толщины h, модуля упругости Е, коэффициента Пуассона ν, поверхностной массы μ, скорости звука в воздухе со = 344 м/с, коэффициента внутренних потерь η.
Определению искомых значений звукоизоляции по вышеизложенной методике (см. подразд. 5.2) предшествуют предварительные расчеты граничных частот расчетных областей, которые выполняются в соответствии с блоком 4.
Блок 5 характеризует начало цикла последовательности вычислений
усредненных характеристик звукоизлучения S и построение частотной характеристики звукоизоляции R(f) в 21 частотном диапазоне. Блоки 8 и 16 осуществляют проверку на окончание цикла (конец частотного диапазона анализа).
В соответствии с элементом 6 блок-схемы осуществляется выбор среднегеометрической частоты соответствующей наименьшей граничной частоте области простых пространственных резонансов.
Блоки 9 и 10 осуществляют ветвление вычислительного процесса по различным расчетным формулам в зависимости от ранее вычисленных граничных частот. Вычисление значений звукоизоляции в области простых пространственных резонансов ведется по формулам (5.18), (5.21) (блок 11), в области неполных пространственных резонансов по формулам (5.19), (5.22) (блок 12) и в области полных пространственных резонансов по формулам (5.20), (5.23) (блок 13).
На печать выводятся значения среднегеометрических частот F(I), соответствующие им значения звукоизоляции R(I) (блок 14).
Результаты расчетов, выполненных по предложенному алгоритму, приведены на рис. 5.4-5.7. Сопоставление экспериментальных кривых звукоизоляции с расчетными говорит о хорошей их сходимости и возможности использования разработанной методики расчета звукоизоляции ограждений с ребрами жесткости в инженерной практике.
118

Рис. 5.4. Частотные характеристики звукоизоляции пластины из дюралюминия толщиной 1,5 мм с тремя ребрами жесткости на заклепках (Шз = 240 мм):
1 – теоретическая; 2 – экспериментальная
Рис. 5.5. Частотные характеристики звукоизоляции пластины из дюралюминия толщиной 1,5 мм с пятью ребрами жесткости на заклепках (Шз = 60 мм):
1 – теоретическая; 2 – экспериментальная; 3 – теоретическая [7]
119
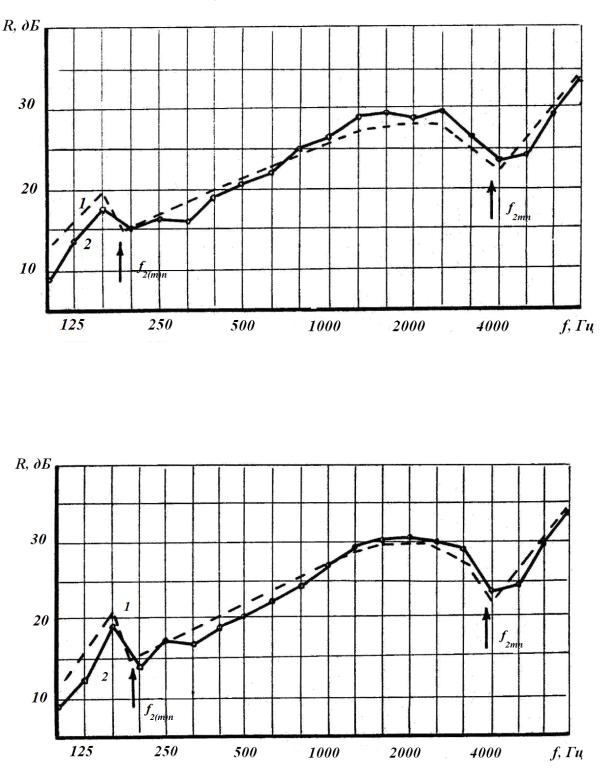
Рис. 5.6. Частотные характеристики звукоизоляции пластины из стали толщиной 3,0 мм с двумя ребрами жесткости на сварке:
1 – теоретическая; 2 – экспериментальная
Рис. 5.7. Частотные характеристики звукоизоляции пластины из стали толщиной 3,0 мм с одним ребром жесткости на сварке:
1 – теоретическая; 2 – экспериментальная
120
