
1990
.pdf
Таким образом, длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчёта, относительно которой эта точка неподвижная.
Поэтому часы движущиеся относительно инерциальной системы отсчёта, будут идти медленнее покоящихся часов. Другими словами, ход часов замедляется в системе отсчёта, относительно которой часы движутся.
3. Длина тел в разных системах отсчёта.
Рассмотрим стержень, расположенный вдоль оси x и покоящийся относительно системы K . Длина данного стержня в системе K будет равна
l0 x2 x1 , где x1 и x2 – не изменяющиеся со временем t координаты
начала и конца стрежня. Индекс 0 указывает , что в системе K стержень покоится.
Определим длину этого стрежня в системе K, относительно которой он движется со скоростью . Для этого необходимо измерить координаты его концов x1 и x2 в системе K в один и тот же момент времени t. Их Разница
этих координат равна длине стержня в системе K l x2 x1 .
l x x |
x2 t |
|
x1 t |
|
x2 x1 |
l |
|
l |
. |
|||
|
|
|
|
|
||||||||
0 |
2 |
1 |
1 |
2 |
|
1 2 |
|
1 2 |
0 |
1 |
2 |
|
|
|
|
|
|
|
|||||||
Заключение:
Линейный размер тела, движущегося относительно инерциальной системы отсчёта уменьшается в направлении движения. Величина
уменьшения, зависящая от скорости движения системы отсчёта K
относительно системы отсчёта K равна 1 2 |
|
1 2 / c2 . |
Лоренцево сокращение длины тела тем больше, чем больше скорость его движения .
Поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчёта.
Релятивистский закон сложения скоростей можно обосновать
анализом материальной точки движущейся в инерциальной системе K
|
|
|
когда K |
движется относительно инерциальной |
||||||||
вдоль оси x при условии, |
||||||||||||
системы K со скоростью . |
|
|
|
|
|
|
|
|
|
|
||
Уравнения для скоростей движения точки в системах K и K имеют вид |
||||||||||||
|
|
|
u |
x |
dx |
, |
u |
dx |
, |
|||
|
|
|
|
|
dt |
|
|
x |
dt |
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
, dt dt |
|
dx |
|
/ c |
2 |
. |
|
|||
где dx dx dt |
|
|
|
|
|
|
||||||
1 2 |
|
|
|
|
|
|
1 2 |
|
|
|
|
|
41
Из данных уравнений получаем соотношения при переходах от одной системы отсчёта к другой:
|
K K : ux |
ux |
и K K : ux |
ux |
||
|
|
|
|
. |
||
|
1 ux / c2 |
1 ux / c2 |
||||
Если принять, что скорость точки в системе K равна скорости света |
||||||
ux с, |
то и скорость точки в системе K также станет равной скорости света |
|||||
ux с. |
Таким образом, |
уравнения |
описывающие релятивистский закон |
|||
сложения скоростей, не противоречат второму постулату Эйнштейна указывающему, что скорость света c – предельная скорость, которую невозможно превысить.
Если скорости точки малы по сравнению со скоростью света ux c , ux c , а также скорость c , то полученные уравнения для скоростей
переходят в уравнения, описывающие закон сложения скоростей в классической механике:
K K : |
ux ux и K K : |
ux ux . |
Данные соотношения являются преобразованиями Галилея.
Интервал между событиями.
Дляисследованиясобытий, происходящихвПриродеА. Эйнштейнввёл понятие четырёхмерного пространства и установил существование инвариантности по отношению к преобразованиям его координат.
Каждое событие, связанное с материальными объектами в таком пространстве, характеризуется четырьмя координатами x , y , z и t .
Согласно Эйнштейну интервал между событиями s12 определяется относительно инерциальной системы отсчёта K уравнением
s12 c2 (t2 t1)2 (x2 x1)2 (y2 y1)2 (z2 z1)2 ,
где l12 (x2 x1)2 (y2 y1)2 (z2 z1)2 – расстояниемеждуточкамиобычного трёхмерного пространства, в которых эти события произошли.
Вводим обозначение t12 t2 t1 и получаем более компактное уравнение
для интервала между событиями относительно инерциальной системы отсчёта K
s12 c2t122 l122 .
Интервал между событиями относительно инерциальной системы
отсчёта K равен s12 |
|
c |
t12 |
l12 . |
|
|
2 |
2 |
2 |
Используя отдельные уравнения для пространственных и временных интервалов, записываемых относительно инерциальных систем отсчёта K и
42

K , и учитывая связи между ними, установленные преобразованиями Лоренца, можно получить равенство интервалов между событиями относительно инерциальных систем отсчёта K и K
s12 s12 .
Это соотношение указывает, что интервал между событиями в четырёхмерном пространстве Эйнштейна является инвариантной величиной по
отношению к преобразованию инерциальных систем отсчёта K и K . Инвариантность связана с независимостью интервала между событиями s12
от системы отсчёта.
Заключительные выводы:
Теория относительности сформулировала новое представление о пространстве и времени:
Пространство – временные отношения являются не абсолютными величинами, как утверждала механика Галилея – Ньютона, а относительными. Следовательно, представления об абсолютном пространстве и времени являются несостоятельными.
Инвариантность интервала между двумя событиями s12 свидетель-
ствует о том, что пространство и время органически связаны между собой и образует единую форму существования материи – пространство – время.
Пространство и время не существуют вне материи и независимо от неё.
Релятивистский импульс микрочастицы по закону релятивистской динамики определяется из уравнения
|
m |
|
р |
|
, |
1 2 / c2 |
где m , – масса и скорость микрочастицы.
Закон сохранения релятивистского импульса:
Релятивистский импульс замкнутой системы сохраняется, т.е. не изменяется с течение времени. Этот закон является фундаментальным законом в связи с тем, что он обоснован однородностью пространства.
Свойство однородности геометрического пространства проявляется в неизменности физических законов, описывающих поступательное движение материальных объектов при параллельном переносе объекта или системы объектов рассматриваемой как целостный объект.
Другими словами, однородность пространства связана с независимостью физических законов, описывающих поступательное движение материальных объектов от выбора начала систем координат инерциальных систем отсчёта.
43

Основной закон релятивистской динамики
Согласно принципу относительности Эйнштейна, утверждающему инвариантностьвсехзаконовприродыприпереходеотоднойинерциальной системы отсчёта к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца.
При таких обстоятельствах основной закон релятивистской динамики описывает уравнение для силы в форме:
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
d p |
|
m |
|
||||
|
|
F |
|
dt |
|
|
|
|
|
, |
|
|
dt |
1 2 / c2 |
|||||||
где |
|
|
|
|
|
|
|
|
|
|
р |
m – релятивистский импульс микрочастицы. |
|||||||||
Данное уравнение инвариантно по отношению к преобразованиям
Лоренца и, следовательно, оно удовлетворяет принципу относительности
Эйнштейна. Кроме этого, следует учитывать, что импульс р и сила F не
являются инвариантными величинами. Из приведённых выше уравнений следует, что при скоростях c данные уравнения переходят в уравнения классической механики.
Выводы:
Неравенство c необходимотолковатькакусловиеприменимости законов классической механики;
Законы классической механики являются следствием специальной теории относительности для предельного случая c ;
Классическая механика– это механика макротел, движущихся с малыми скоростями по сравнения со скоростью света c .
Полная энергия релятивистской частицы в релятивистской динамике:
E |
Е |
/ c2 |
|
m с2 |
, |
|
1 2 |
1 2 |
/ c2 |
||||
|
0 |
|
|
0 |
|
|
где Е0 , m0 , – энергия покоя, масса покоя и скорость микрочастицы. Энергия покоя равная Е0 m0с2 и масса покоя m0 определяются относи-
тельно системы отсчёта K , в которой микрочастица не движется.
Полная энергия релятивистской частицы в разных системах отсчёта различна.
Уравнение для полной энергии, записанное выше, является универсальным. Данное уравнение устанавливает, что с любой энергией E в природе какой бы формы она не была, всегда связана масса m и, наоборот, со всякой массой m в природе всегда связана определённая энергия E.
44
Полная энергия в релятивистской динамике равна сумме кинетической энергии T и энергии покоя
E E0 T .
Полная энергия в классической механике равна сумме потен-
циальной и кинетической энергии
E П T .
Закон сохранения энергии:
Полная энергия замкнутой системы сохраняется, т.е. не изменяется с течением времени t. Этот закон является фундаментальным, так как он обусловлен однородностью времени.
Однородность времени необходимо толковать как инвариантность физических законов относительно выбора начала отсчёта времени (нуль времени).
Кинетическая энергия релятивистской частицы T оценивается с учётом её полной энергии E, описываемой уравнением
|
|
E E0 T , |
|
|
|
|
||
T E E0 |
Е |
|
E0 |
m0с |
2 |
|
1 |
|
0 |
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
1 2 / c2 |
|
|
|
1 2 / c2 |
|||
Связь между энергией и импульсом
Энергия и импульс в разных системах отсчёта различна. Однако, установлено, что существует инвариантная величина
E2 p2c2 inv ;
|
E |
2 |
2 |
c |
2 |
|
|
m2c4 |
2 |
2 |
c |
2 |
2 |
4 |
|
2 |
|
|
|||
|
|
p |
|
1 2 |
/ c2 m |
|
|
m0 c |
|
E0 , |
|
|
|||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E2 m2c4 |
p2c2 . |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
С учётом уравнения для полной энергии E T E |
T m c2 |
получаем |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
E2 (T m c2 )2 |
, (T m c2 )2 |
m2c4 p2c2 исоотношение pc |
T (T 2m c2 ) . |
||||||||||||||||||
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
||
Отсюда релятивистский импульс определяется из уравнения |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
T (T 2m c2 ) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
p |
|
|
|
|
0 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45
2. ЭЛЕКТРИЧЕСТВО И ЭЛЕКТРОМАГНЕТИЗМ
2.1. Электростатика
Электрический заряд Q – скалярная мера микрочастиц и макротел, характеризующаяихспособностьучаствовать во взаимодействиях, которые обусловлены электромагнитным полем.
Замкнутая система электрических зарядов – система, не участву-
ющая в обмене зарядами с внешними заряженными телами.
Фундаментальные свойства электрических зарядов Q:
Элементарными носителями электрического заряда равного
е qe qp 1,6 10 19 Кл являются микрочастицы электрон 10e и протон 10 р
(заряженное ядро атома водорода 01H ),
Электрические заряды имеют разные знаки (отрицательный Q 0 у
электрона 10e и положительный Q 0 у протона),
Электрические заряды инвариантны. В любых инерциальных и неинерциальных системах отсчета величина заряда одинакова,
Электрические заряды изменяются дискретными порциями равными
заряду электрона или протона е q |
q |
p |
1,6 10 19 Кл. Величина заряда |
e |
|
|
|
для любых тел (частиц) оценивают |
из уравнения Q ze , где |
||
z 0, 1, 2, 3, ..., N , N – число заряженных тел (частиц) системы.
Электрические заряды аддитивны. Общий заряд системы заряжен-
|
N |
ных тел (частиц) описывается алгебраическим уравнением |
Q Qi , где |
|
1 |
N– число заряженных тел (частиц) системы.
Электрические заряды сохраняются. Алгебраическая сумма электри-
ческих зарядов при любых их перераспределениях в замкнутой системе
N
зарядов является постоянной величиной Q Qi const . Другими слова-
1
ми, изменение общего заряда с учётом их знака внутри замкнутой системы зарядов равно нулю Q 0.
Точечный заряд – физическая модель заряда, сосредоточенного на макротеле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием r до других заряженных макротел, с которыми он взаимо-
действует. |
|
|
|
||
По закону Кулона векторы и модули сил взаимодействия F |
между |
|
двумя неподвижными точечными зарядами Q1 и Q2 , находящимися в вакууме ( 1) или в однородной и изотропной диэлектрической среде ( 1)
46
пропорционален зарядам и обратно пропорционален квадрату расстояния r между ними:
|
|
|
|
|
1 |
|
|
|
Q |
|
|
|
Q |
|
|
|
|
|
|
r |
|
|
1 |
|
|
|
Q |
|
|
|
Q |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
F |
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
r |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
r2 |
|
r |
|
|
|
|
|
|
r2 |
||||||||||||||||||||||||||||
|
|
12 |
|
|
4 0 |
|
|
|
|
|
|
4 0 |
|
|
|
e |
||||||||||||||||||||||||||||||
|
|
и |
F |
|
= |
|
1 |
|
|
|
|
|
Q1Q2 |
|
|
, |
F |
|
= |
|
1 |
|
|
|
|
|
|
Q2Q1 |
|
, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
4 0 |
|
|
|
|
|
r2 |
|
|
|
4 0 |
|
|
|
|
|
|
r2 |
|
|
||||||||||||||||||||||||
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
где |
12 |
|
ф |
– фундаментальная |
|
физическая электрическая |
||||||||||||||||||||||||||||||||||||||||
0 =8,85 10 |
|
м |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
постоянная. Векторы сил |
|
F12 |
|
и |
|
|
|
F21 |
|
направлены по прямой, соединяющей |
||||||||||||||||||||||||||||||||||||
взаимодействующие заряды. Поэтому эти силы считают центральными.
Согласно 3 закону Ньютона F12 = F21 и F12 = F21 . Притяжение разно-
именных зарядов соответствует положительному знаку модулей сил, а отталкивание – отрицательному знаку.
|
Диэлектрическая проницаемость среды – безразмерная величина, |
|||||||||||||||
определяемаизуравнения |
F |
, где F , F – соответственно, силывзаимо- |
||||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
F0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
действия между зарядами в заданной среде и в вакууме. |
||||||||||||||||
|
Электростатическое поле – поле, создаваемое электрическими заря- |
|||||||||||||||
дами, скорость которых равна Q 0. |
|
|
|
|
||||||||||||
|
Напряженность электростатического поля точечных зарядов – |
|||||||||||||||
векторная |
силовая |
физическая |
величина, |
определяемая из уравнений |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
F |
F |
|
|
|
|
|
|||||||||
Е |
|
21 |
и |
E |
|
12 |
, |
где Е |
F |
, Е |
2 |
F |
, Q |
и Q – точечные пробные |
||
1 |
|
Q2 |
2 |
Q1 |
1 |
21 |
|
12 |
1 |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
положительные заряды малые по величине и помещаемые в заданные точки поля. Пробные заряды не должны искажать исследуемое поле путём перераспределения зарядов, создающих это поле.
Модули напряженностей полей создаваемых точечными зарядами Q1 и Q2 в вакууме определяют из уравнений
Е |
1 |
|
Q1 |
и |
Е |
|
|
1 |
|
Q2 |
, |
|
|
|
|||||||||
1 |
4 0 |
r2 |
|
|
2 |
|
4 0 |
r2 |
|
||
где r – радиусы векторы, соединяющие данную точку поля с зарядом.
Направление вектора напряжённости поля Е совпадает с направлением силы, действующей на положительный заряд. Если поле создается
положительным зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положительного
47
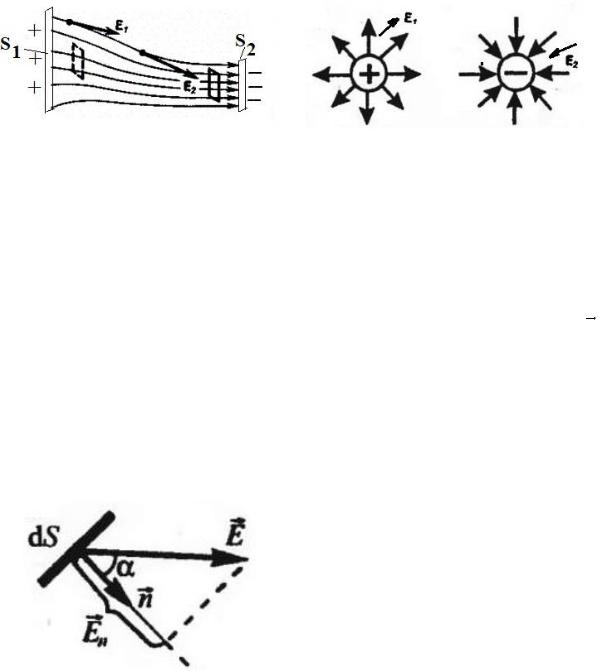
заряда). Если поле создается отрицательным зарядом, то вектор Е направлен к заряду (рис. 24).
Линии напряженности электростатического поля. Поток вектора напряженности поля
Линии напряженности поля (силовые линии) – это криволинейные
или прямолинейные линии, касательные к которым в каждой точке поля |
||
|
|
определяется |
совпадают с направлением вектора Е |
(см. рис. 24). Модуль Е |
|
густотой линий поля Линии выходят из положительных зарядов, и входят в отрицательные заряды
Рис. 24
Плоские заряженные поверхности с S1 S2 и одиночные точечные заряды формируют неоднородные электрические поля. Линии параллель-
ные друг другу характеризуют однородные поля. Вектор Е в любой точке такого поля постоянен по модулю и направлению.
Поток векторного поля ФE – скалярная характеристика электростатического поля, определяемая числом линий, пронизывающих единицу пло-
щади поверхности, перпендикулярно линиям поля Е. Поток вектора Е сквозь произвольную замкнутую поверхность S произвольной формы оценивают интегральным уравнением
|
|
|
|
|
|
EndS E cos dS , |
|
|||
|
|
|
|
ФE Е |
dS |
|
||||
|
|
|
|
S |
|
S |
S |
|
|
|
где подинтегральное выражение |
Е dS |
– скалярное произведение векторов |
||||||||
|
и |
|
|
Еn E cos – проекция вектора |
|
|
|
|||
Е |
dS |
dS n , |
Е на направление вектора |
|||||||
|
|
|
|
|
|
нормали поверхности n , |
– угол |
|||
|
|
|
|
|
|
между вектором Е и вектором нор- |
||||
|
|
|
|
|
|
мали поверхности n . |
|
|||
|
|
|
|
|
|
|
Поток |
ФE |
зависит |
от конфи- |
|
|
|
|
|
|
гурации поля Е |
и от выбора направ- |
|||
ления n (рис. 25).
Рис. 25
48
Принцип суперпозиции (наложения) электростатических полей: |
|||||||
Напряженность |
|
|
результирующего поля, создаваемого системой |
||||
Е |
|
||||||
точечных зарядов |
в |
|
данной |
точке, |
равна |
геометрической сумме |
|
напряженностей полей |
|
|
, создаваемых каждым из зарядов Q1 , Q2 , Q3 …, |
||||
|
E i |
||||||
|
|
n |
|
|
|
|
|
Qn в отдельности Е |
Еi |
= E1 |
+ E 2 + |
E 3 …..+ |
E n . |
||
i 1
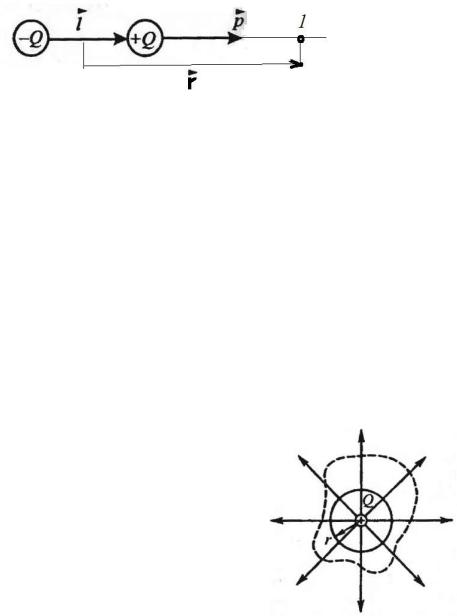
Электрический диполь – система из двух равных по модулю разноименных точечных зарядов, расстояние между которыми значительно меньше расстояния до рассматриваемых точек поля.
Электрический момент диполя р Ql – вектор, совпадающий по направлению с ориентированным плечом диполя l (рис. 26).
Рис. 26
Напряженность поля диполя на продолжении его оси в произвольной точке 1 равна
|
|
|
|
|
Е |
|
|
|
1 |
|
2 р |
, |
|
|
|
|
|
|
|
|
r3 |
||||
|
|
|
|
|
1 |
|
|
4 0 |
|
|||
|
n |
|
|
|
|
|
|
|
|
|
||
где Е1 |
Еi |
E |
+ E |
, E |
< |
E |
|
– напряжённости полей, создаваемые в |
||||
i 1
точке 1, соответственно, зарядами Q и Q .
Теорема Гаусса для электростатического поля в вакууме:
Поток вектора Ё сквозь произвольную поверхность равен
|
|
|
1 |
n |
1 |
|
||
ФE E |
dS |
EndS |
|
|
Qi |
|
|
Q . |
|
0 |
|
0 |
|||||
S |
|
S |
|
i 1 |
|
|
||
Этот результат справедлив для замкнутой поверхности любой формы. Если окружить сферу (рис. 27) произвольной замкнутой поверхностью, то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.
Рис. 27
49
|
Величина заряда, создающего поле, может зависеть от длины тела |
|||||||||||
Q |
|
1 |
dl , |
поверхности тела |
Q |
1 |
dS или объёма тела |
Q |
|
1 |
dV , |
|
|
|
0 |
|
|||||||||
|
|
0 l |
|
|
|
S |
|
|
0 V |
|||
где |
|
dQ |
; dQ |
; dQ |
– объёмная, поверхностная |
и |
линейная |
|||||
|
|
|
dV |
dS |
dl |
|
|
|
|
|
|
|
плотности электрического заряда; dl , dS и dV – соответственно, элементы длины поверхности и объёма заряженного тела.
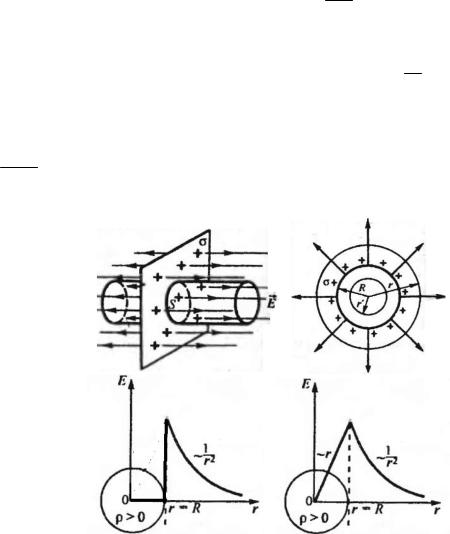
Следствия из теоремы Гаусса:
1. Напряжённость поля в пространстве вокруг равномерно заряженной
бесконечной плоскости в вакууме равна E . 2 0
2. Напряжённость поля в пространстве внутри двух равномерно заря-
женных бесконечных плоскостей в вакууме равна E .
0
3. Напряжённости поля в пространстве вокруг равномерно заряженных сферической поверхности и объемно заряженного шара при r R равны
Е 4 1 0 rQ2 и отличаются при r R (см. графики (рис. 28)).
Рис. 28
Циркуляция вектора напряженности электростатического поля
вдоль замкнутого контура L, окружающего электрический заряд Q , равна |
||||
|
ГE = |
|
|
El dl 0 . Силовое поле обладающее таким свойством |
нулю |
Е |
dl |
||
|
L |
|
|
L |
называют потенциальным.
50
