1990

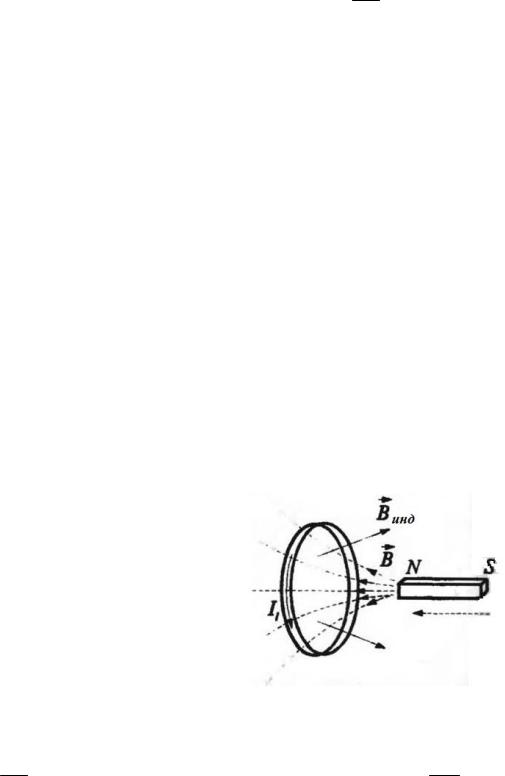
Правило Ленца

Из анализа формы записи закона Фарадея инд ddt можно сделать

вывод о том, что знак ЭДС индукции инд противоположен знаку изменения

внешнего магнитного потока .

Если внешний магнитный поток BS , пронизывая поверхность пересекаемую проводником, увеличивается 0 , то ЭДС индукции

отрицательная по знаку инд 0. Индукционный ток в проводнике, возни-

кающий под действием этой ЭДС индукции, создаёт собственный магнитный поток инд ВиндS , изменение которого препятствует увеличению

внешнего магнитного потока .

Если внешний магнитный поток BS , пронизывая поверхность пересекаемую проводником, уменьшается 0 , то ЭДС индукции

положительнаяпознаку инд 0, тоиндукционныйтоквпроводнике, возни-

кающий под действием этой ЭДС индукции, создаёт собственный магнитный поток инд ВиндS , изменение которого препятствует уменьшению

внешнего магнитного потока BS .

Поэтому знак минус в законе Фарадея необходимо рассматривать как математическое подтверждение правила Ленца. Это правило является общим правилом для оценки направления индукционного тока:

Индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток.

Поэтому при приближении плоскогомагнитакзамкнутомупроводнику, охватывающему поверхность S (рис. 56), скорость изменения внешнего магнитного потока положительная по знаку

d d(BS) SdB 0 , d 0 , dB 0 . dt dt dt

Отсюда магнитная индукция В внешнего поля положительная по знаку и увеличивается.

ЭДС индукции, возникающая в замкнутом проводнике по закону Фарадея инд ddt , создаёт в проводнике индукционный ток Iинд Rинд . Скорость изменения магнитного потока сформированного индукционным то-

91

таких условиях магнитная индукция поля индукционного тока отрицательная по знаку Bинд 0 и уменьшает магнитную индукцию внешнего

поля В.

При удалении плоского магнита от замкнутого проводника магнитная индукция поля индукционного тока положительная по знаку Bинд 0 и

увеличивает магнитную индукцию внешнего поля В.

Направление вектора магнитной индукции поля индукционного тока

Винд определяется по правилу правого винта.

ЭДС индукции в неподвижных проводниках

ЭДС электромагнитной индукции, оцениваемая по закону Фарадея из соотношения инд ddt , возникает и в неподвижном проводящем контуре

помещённом в переменное магнитное поле B В(t) .

Однако, возникновение ЭДС индукции инд нельзя объяснить на основе

силы Лоренца. Эта сила на свободные заряды (электроны) в неподвижном проводнике не действует.

Данное явление в неподвижных проводниках Максвелл обосновал существованием неразрывной связи между магнитным и электрическим

Привращениирамкиводнородномпостоянном магнитном поле B В(t) с угло-

войскоростью const магнитныйпоток, сцепленный с рамкой площадью S в любой момент времени описывается уравнением

m cos BnS BS cos t ,

92

По закону Фарадея при вращении рамки в ней возникает переменная

значение ЭДС индукции. Таким образом, ЭДС индукции колеблется по гармоническому закону описываемому уравнением инд m cos t .

Явление, происходящее при вращении плоской рамки в однородном магнитномполе, былоположеновосновупринципаработыпромышленных

генераторов переменной ЭДС инд m cos t . Такие генераторы играют

важную роль в развитии любой страны. Они выполняют роль источников электрической энергии вырабатываемой за счёт преобразования механической энергии в энергию электрического тока I.

Для увеличения максимального значения ЭДС индукции max ВS в

промышленных генераторах переменной ЭДС используют ряд витков, соединенных последовательно, которые увеличивают площадь S.

Переменное напряжение U Um cos t практически равное ЭДС индукции инд U (внутреннее сопротивление проводников рамки малое r R )

формируется на двух кольцах укреплённых на концах витков рамки. К кольцам прикреплены неподвижные проводящие щетки и клеммы источника переменного напряжения U Um cos t .

Вихревые токи (токи Фуко) – это индукционные токи возникающие в массивных сплошных проводниках, помещенных в переменное магнитное поле. Данные токи замкнуты в толще проводника и поэтому их называют вихревыми токами.

Согласно правилу Ленца магнитное поле, создаваемое этими токами, направлено так, чтобы противодействовать любому изменению внешнего магнитного потока, который обуславливает их возникновение.

Этот вывод подтверждается на примере сильного торможения и быстрой остановки массивного медного маятника, совершающего практически незатухающие колебания в пространстве между магнитными полюсами N и S подковообразного соленоида. Такое явление возникает при условии подключения концов его обмотки к источнику постоянного напряжения и возникновения тока I.

Индуктивность проводящего контура L – коэффициент пропорцио-

нальности между магнитным потоком и силой тока I.

Индукция магнитного поля B, создаваемого током по закону Био – Савара – Лапласа, пропорциональна силе тока I. Поэтому сцепленный с проводящим контуром магнитный поток определяется из уравнения LI .

Индуктивность проводящего контура в общем случае зависит только от геометрической формы проводящего контура, его размеров и магнитной проницаемости той среды, в которой он находится.

93

Самоиндукция – явление, связанное с возникновением ЭДС индукции в проводящем контуре при изменении в нём силы тока.

ЭДС самоиндукции можно оценить по закону Фарадея

где L – постоянный параметр названный самоиндукцией и независимый от тока I. Величина L остаётся неизменной при постоянной форме проводника

и постоянной магнитной проницаемости среды окружающей его.

Знак минус, обусловленный правилом Ленца, показывает, что наличие индуктивности вконтуреприводит куменьшениюскорости изменениятока

dIdt и замедлению тока в нём. Если ток возрастает, то dIdt 0 , а ЭДС

самоиндукции сами 0 . При отрицательной знаке сами ток самоиндукции

направлен навстречу току, обусловленному внешним источником магнитного поля, и тормозит его возрастание.

Индуктивность соленоида

Полный магнитный поток сквозь соленоид (потокосцепление)

NBS 0 N 2 I S . Отсюда индуктивность соленоида l

L 0 Nl2 I ,

где N – число витков; l – длина соленоида; S – площадь; 0 и – магнитная

постоянная и магнитная проницаемость среды внутри соленоида. Токи при размыкании и замыкании цепи

Экстратоки самоиндукции Iсами – это дополнительные токи, возникающие за счет ЭДС самоиндукции сами при отключении и подключении

источника постоянной ЭДС . Данные токи направлены противоположно основному току, создаваемому источником постоянной ЭДС .

Переменные токи при размыкании и замыкании электрической цепи постоянного тока возникают в электрической цепи (рис. 58).

Рис. 58

94

1. При размыкании ключа Кл происходит отключение источника постоянной ЭДС и в момент времени t0 0 возникает ЭДС самоиндукции

сами L dIdt . Эта ЭДС препятствует быстрому уменьшению начального

значения силы тока I0 , поддерживаемого до отключения источником постоянной ЭДС . Ток в цепи определяется законом Ома описывают уравне-

ния I самиR , IR L dIdt , RL dt dII . Проводим операцию интегрирования и получаем уравнение для переменного тока в форме I I0 exp( t / ) , где

L / R – время релаксации, за которое сила тока уменьшается в е раз. Ход тока от времени изображён на рис. 58 кривой линией 1. Таким

образом, сила тока при размыкании цепи не мгновенно спадает до нуля, а убывает по экспоненциальному закону.

Следует знать, что ЭДС самоиндукции сами, возникающая в цепи

содержащей проводящий контур с большим значением L при условии быстрого отключении одной клеммы источника постоянной ЭДС , может во много раз превысить . При таком обстоятельстве экстраток самоиндукцииможетрасплавитьпроводящийконтур, ачеловекможетбыть подключён к опасному источнику высокого напряжения. Поэтому такой контур нельзя резко размыкать.

2. При замыкании ключа Кл в цепи действуют два источника ЭДС исами L dIdt . Причём ЭДС самоиндукции сами препятствует мгновенному

тока от времени изображён на рис. 58 кривой линией 2.

Таким образом, при замыкании электрической цепи ток достигает предельного значения I0 / R не мгновенно, а постепенно.

Взаимная индукция – явление, связанное с возникновением ЭДС в одном из проводящих контуров при изменении силы тока в другом.

Еслидвапроводящихконтура1 и2 стоками I1 и I2 расположеныблизко друг к другу (рис. 59), то при наличии в контуре 1 тока I1 магнитный поток

(его поле на рисунке изображено сплошными линиями) пронизывает второй контур: 2 LI1 . С другой стороны, справедливо такжеи уравнение 1 LI2

.

95

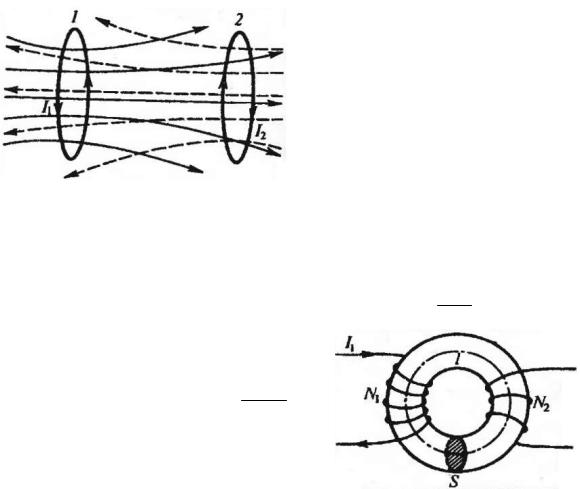
Коэффициенты L, которые одинаковые в обоих уравнениях, названы взаимной индуктивностью контуров. Величина L зависит от геометрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости среды

окружающей контуры.

ЭДС индукции возбуждаемые в каждом контуре по закону Фарадея равны

Взаимная индуктивность двух катушек, намотанных на тороидаль-

ный сердечник (рис. 60) оценивается с учётом уравнения для магнитного потока сквозь один виток второй катушки 2 BS 0 Nl1I1 S .

Полный магнитный поток (потокосцепление) сквозь N2 витков вторичной

обмотки равен 2 N2 0 N1lN 2 SI1 . Поток создается током I1 поэтому

Энергия магнитного поля, сцепленного с проводящим контуром локализована в пространстве.

Если какой-либо проводящий контур, обладающий индуктивностью L,

подключён к источнику постоянной ЭДС , то в нём возникает постоянный макроток I и сцепленный с ним постоянный магнитный поток LI . Индуктивность L постоянная величина, зависящая от формы контура и среды его окружающей. Поэтому бесконечно малое изменение магнитного потока d определяется бесконечно малым изменением тока dI : d LdI .

96

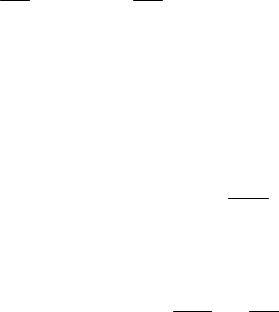
где Wм0 LI202 0 и Wм1 LI212 – начальное и конечное значение энергии

магнитного поля.

Таким образом, работа источника ЭДС израсходована на изменение

энергии магнитного поля А1 W1 Wм1 Wм0 Wм1 0 Wм1 .

Постоянная энергия магнитного поля соленоида определяется его

W1 0 N 2 I 2 S . 2 l

Согласно теореме о циркуляции индукции магнитного поля в соленоиде Вl 0 I , I Bl( 0 N) и уравнения В 0 Н получаем

W В2 I 2 Sl ВH V , 2 0 2

где V Sl – объём пространства внутри соленоида.

Объемная плотность энергии соленоида

Магнитное поле соленоида внутри него однородное и поэтому энергия магнитного поля сосредоточена в его внутреннем объеме и распределена в нём с объемной плотностью равной

Трансформатор – это статический электромагнитный аппарат, осуществляющий преобразование электрической энергии в цепи переменного тока с одним значением ЭДС 1 m1 cos t , напряжения U1 Um1 cos t и

тока I1 Im1 cos t в электрическую энергию с другим значением ЭДС

2 m2 cos t , напряжения U2 Um2 cos t и тока I2 Im2 cos t при сохранении неизменной циклической частоты ЭДС, напряжений и токов

2 const .

Устройствотрансформатора, показанноениженарисунке, содержитдве проводящие обмотки с числом витков N1 и N2 , которые намотаны на

магнитопроводящий сердечник из электротехнической стали. К концам 1 и 1 первичной обмотки подключён первичный источник электрической энергии 1 U1 , а на концах 2 и 2 вторичной обмотки возникает вторичный источник электрической энергии 2 U2 (рис. 61).

Работа трансформатора основана на явлении взаимной индукции. ПеременнаяЭДС 1 1 (t) создаетвпервичнойобмоткесчисломвитков N1

97

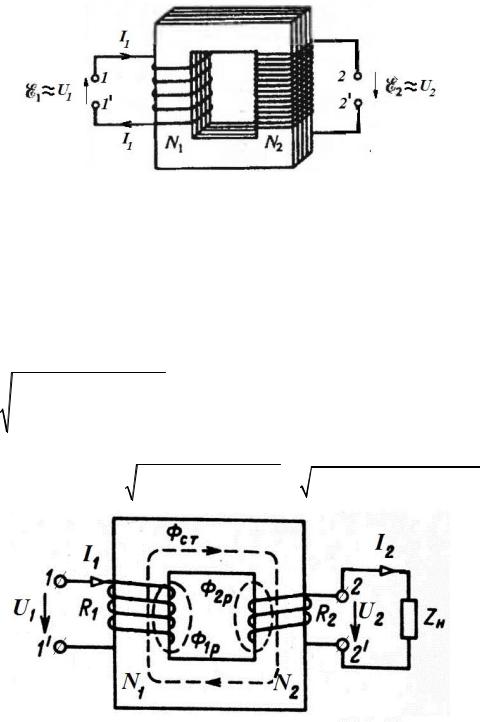
переменный ток I1 I1(t) , который возбуждает в магнитопроводе основной переменный магнитный поток магнитный поток СТ СТ (t) . Этот поток

магнитного поля пронизывает поверхности охватываемые витками первой и второй катушки и по закону Фарадея возбуждает в первой из них ЭДС самоиндукции 1сам, а во второй – ЭДС индукции 2инд .

Рис. 61

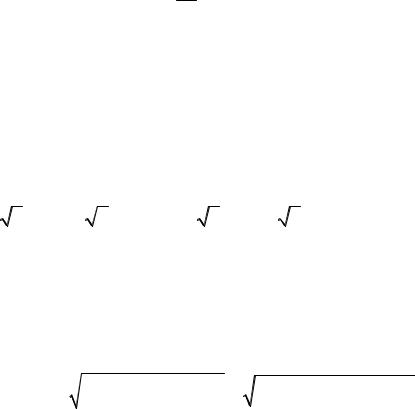
На электромагнитной схеме трансформатора, приведенной на рис. 62, указаны напряжения, силы токов, сопротивления и магнитные потоки для первичной и вторичной обмоток и приёмник электрической энергии Z Н

(нагрузка) подключенный ко вторичной обмотке трансформатора.

При резонансе в цепи вторичной обмотки собственная частота колебаний и частота вынуждающей ЭДС одинаковые

Рис. 62

98

По закону Фарадея в первичной обмотке возникает ЭДС самоиндукции1сам= N1 d dtCT , а во вторичной – ЭДС индукции 2инд = N2 d dtCT . Согласно

2 закону Кирхгофа для замкнутых контуров первичной и вторичной обмоток по справедливы уравнения:

ющиеся частично в воздухе и сцепленные только с одной из обмоток; L1p ,

Коэффициент трансформации напряжения (передачи напряжения)

оценивают отношением амплитуд напряжения во вторичной обмотке Um2 к

амплитуде напряжения Um1 в первичной обмотке: k Um2

Um1

Амплитуды напряжений связаны с действующими значениями напряжений уравнениями Uд2 Um22 и Uд1 Um21 . Поэтому коэффициент

трансформации напряжения k можно оценивать из уравнения k Uд2 .

Uд1

При k 1 трансформатор увеличивает напряжение, а при k 1 – уменьшает. Если k 1, то напряжение в первичной и вторичной обмотках одинаковые и трансформатор выполняет функцию повторителя напряжения. Повторитель напряжения устраняет электрический контакт между проводниками первичной и вторичной обмоток трансформатора и создаёт электрически независимые цепи переменного тока.

99

Коэффициент полезного действия трансформатора определяется отношением активной мощности сопротивления нагрузки трансформатора Р2 к мощности потребляемой трансформатором из сети Р1 :

Р2 0,95 0,98 .

Р1

Активные мощности Р2 и Р1 зависят от токов во вторичной обмотке и первичной обмотке I2 и I1 , а также от напряжений во вторичной обмотке и первичной обмотке U 2 и U1 :

токов и напряжений.

Оценка данных мощностей тока проводится при условии подключения к вторичной обмотки нагрузки с полным сопротивлением равным омическому сопротивлению ZН RH .

Если полное сопротивление нагрузки складывается из омического и реактивного сопротивления

ZН RН2 X LН XCН 2 RН2 Lн 1 / Сн 2 ,

то активная мощность уменьшается и оценивается из уравнения

напряжения U2 Um2 cos t .

ВысокоезначениеКПДтрансформаторапорядка 1 связаносмалыми

потерями электрической энергии идущей на нагрев проводников обмоток, на нагрев электротехнической стали токами Фуко и на намагничивание и размагничивание вещества магнитопровода.

КПД трансформатора достигает максимума при нагрузке Z Н , которая

обеспечивает равенство между электрическими потерями энергии в проводниках обмоток и магнитными потерями в стали.

100