1990

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пензенский государственный университет

архитектуры и строительства» (ПГУАС)

П.П. Мельниченко

ФИЗИКА

ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ, ЭЛЕКТРИЧЕСТВО И ЭЛЕКТРОМАГНЕТИЗМ, КОЛЕБАНИЯ И ВОЛНЫ

Рекомендовано в качестве учебного пособия для бакалавров по направлению подготовки 23.03.03

«Эксплуатация транспортно-технологических машин и комплексов»

Под общей редакцией доктора технических наук, профессора Г.И. Грейсуха

Пенза 2015

УДК 53

ББК 22.3 М48

Рецензенты: кандидат педагогических наук, доцент Т.В. Ляпина (кафедра «Общая физика и методика обучения физики», ПГУ); кандидат технических наук, доцент Н.А. Очкина (кафедра «Физика и химия», ПГУАС)

Мельниченко П.П.

М48 Физика. Физические основы механики, электричество и электромагнетизм, колебания и волны: учеб. пособие / П.П. Мельничен-

ко. – Пенза: ПГУАС, 2015. – 168 с.

Кратко и доступно изложен учебный материал по разделам «Физические основы механики», «Электричество и электромагнетизм» «Колебания и волны» программы курса «Физика».

Учебное пособие разработано на кафедре «Физика и химия» с учетом компетентностного подхода к процессу обучения и предназначено для усвоения, закрепления и повторения пройденного материала на лекциях, подготовки к экзаменамииспользованияналабораторныхипрактическихзанятияхстудентами направления подготовки 23.03.03 «Эксплуатация транспортно-технологических машин и комплексов». Может быть полезно при обучении на подготовительных отделениях и курсах и в учреждениях общего и среднего образования: гимназиях, лицеях, колледжах, школах.

©Пензенский государственный университет архитектуры и строительства, 2015

©Мельниченко П.П., 2015

2

умений правильно применять законы физики для анализа и решения физических задач; самостоятельно работать с учебной, научной и справочной литературой; осуществлять самооценку и самоанализ на основе самопроверки в процессе выполнения заданий.

Работа с учебным пособием в аудитории под руководством преподавателя в коллективе с другими студентами позволяет овладеть способностью к коммуникации в устной и письменной формах (ОК-5); способностью работать в коллективе (ОК-6).

Внеаудиторная работа (самостоятельное решение задач различного уровня сложности) позволяет овладеть способностью к самоорганизации и самообразованию(ОК-7); навыками работыс дополнительной литературой.

Успешное освоение физических и теоретических основ механики, электрических и электромагнитных явлений, колебательных и волновых процессов позволит выпускнику-бакалавру:

владеть научными основами технологических процессов в области эксплуатации транспортно-технологических машин и комплексов (ОПК 2); уметь применять систему фундаментальных знаний (математических, естественнонаучных, инженерных и экономических) для идентификации, формулирования и решения технических и технологических проблем эксплуатации транспортно-технологических машин и комплексов (ОПК 3). В тексте учебного пособия наиболее важные положения и термины, а также формулировки законов и формулы выделены жирным шрифтом и курсивом. Это способствует более эффективному усвоению материала

студентами.

4

ВВЕДЕНИЕ

Физика изучает наиболее простые и вместе с тем наиболее общие формы движения материи и их взаимные превращения путём введения физических величин.

Материя – это окружающий нас мир и всё объективно существующее вокругнас. Существованиематерииввидевеществаиполяобнаруживается человеком посредством ощущений.

Движение – неотъемлемое свойство материи и способ её существования. Движение в природе связано с всевозможными изменениями материи, начиная от простых перемещений в геометрическом пространстве к более сложным движениям в виде процессов мышления.

Механическая, тепловая и другие виды движения материи присут-

ствуют во всех высших и более сложных формах движения материи (химических, биологических и т.д.), отнесенных к предметам изучения других наук (химии, биологии и др.).

По современным представлениям все взаимодействия в природе осуществляются посредством полей. Поле наряду с веществом является одной из форм существования материи. Физика изучает гравитационные, электромагнитные, ядерные и слабые поля. Одной из важных проблем современной физики является решение задачи по объединению полей в единое поле. Если эта задача будет решена, то это позволит найти элементарные материальные объекты, из которых было построено мироздание на начальной стадии его формирования.

Физические законы следует рассматривать как устойчивые и повторяющиеся объективные закономерности, существующие в природе. Законыобязательноподтверждаютсянаопытахиописываютсяразличными по форме уравнениями для физических величин.

Опыты – это наблюдение исследуемых явлений в точно учитываемых условиях, позволяющих проследить за их ходом и воспроизводством при повторении заданных условий.

Гипотеза – научное предположение, которое выдвигается для объяснения физического явления. Гипотеза превращается в достоверную научную теорию после её проверки на опыте и теоретических обоснований.

Физика

–связана с другими естественными науками и отраслями естествознания (астрономия, геология, химия, биология и др.),

–создала ряд новых смежных дисциплин (астрофизика, геофизика, физическая химия, биофизика и др.)

–заложила основы всех технических наук,

–является базой для создания новых отраслей техники (электронная техника, ядерная техника и др.).

Открытия в области физики и их философское обобщение форми-

руют научное мировоззрение.

5

1. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ

Механика изучает закономерности механического движения и причины, вызывающие или изменяющие это движение.

Механическое движение – это изменение с течением времени взаимного расположения тел или их частей относительно других тел.

Классическая механика (механика Галилея – Ньютона) устанавливает законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме c .

Релятивистская механика – устанавливает законы движения макроскопических тел со скоростями, сравнимыми со скоростью распространения света в вакууме. c .

Квантовая механика устанавливает законы движения микроскопических тел (отдельных атомов и элементарных частиц).

В разделе механики «Кинематика» исследуется движение тел, не рассматривая причины, которые это движение обусловливают.

«Динамика» изучает законы движения тел и причины, которые вызывают или изменяют заданное движение,

«Статика» изучает законы равновесия системы тел используя известные законы движения тел.

1.1. Элементы кинематики

Модели механики:

1.Материальная точка – тело, обладающее массой т, размерами которого l в заданной задаче можно не учитывать. При её использовании облегчается решение практических задач. При расчетах движения планеты Солнца их можно считать материальными точками.

2.Системаматериальныхточекможетпредставлятьлюбоепроизвольное макроскопическое тело или даже несколько тел. На начальном этапе изучают движение одной материальной точки, а затем переходят к анализу движения системы материальных точек в целом.

3.Абсолютно твердое тело ни при каких условиях не может подвергаться деформации под действием внешних сил и расстояние между двумя его материальными точками (точнее между двумя его частицами) остается постоянным.

4.Абсолютно упругоетелодеформируется под действием внешних сил, подчиняющихся закону Гука. После прекращения деформации данное тело принимает свои первоначальные размеры и форму.

5.Абсолютно неупругое тело полностью сохраняет деформированное состояние после прекращения действия внешних сил.

6

Механическое движение материальной точки и тел связано с изменением их положения в геометрическом пространстве во времени. При описании их движений устанавливают размеры области пространства, где они находились в заданные моменты времени, и характеристики движений (скорость, ускорение).

Телом отсчета механического движения это произвольно выбранное тело, относительно которого определяется положение других движущихся тел.

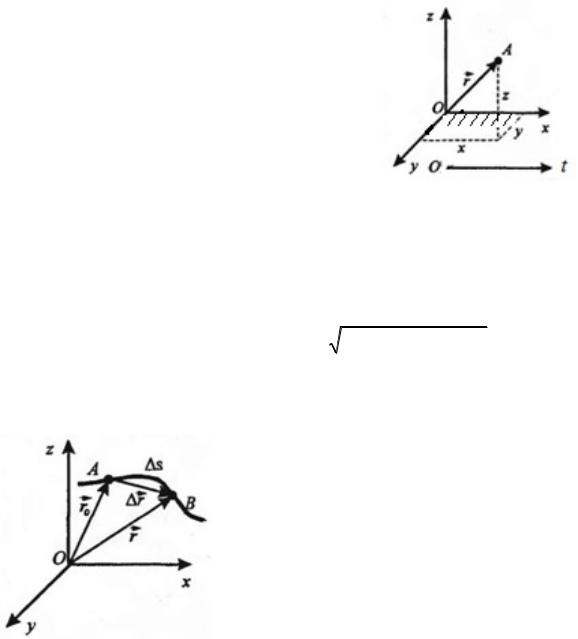
Системакоординат, жёсткосвязаннаястеломотсчетаопределяетмеры геометрического пространства. В простейшем случае (рис. 1) используют прямолинейную декартову систему координат (x, y, z) .

Траектория – линия, вдоль которой движется материальная точка (или центр массы тела) относительно избранной системы отсчета. В зависимости отформытраекторииразличаютпрямолинейноедвижениеикриволинейное

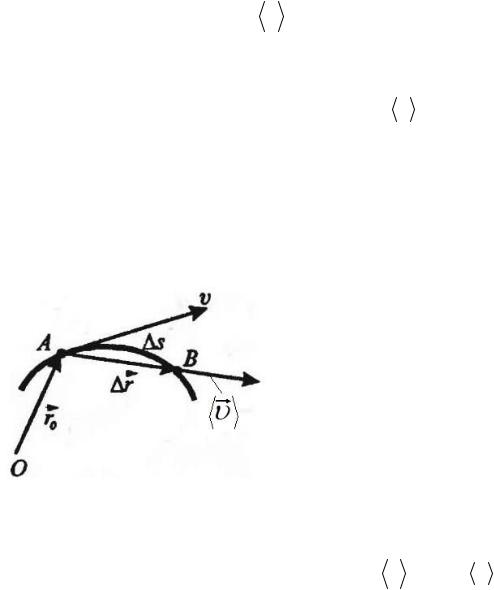
вектора определяющего начальное положение (А) до конца вектора определяющего конечное положение (В) движущейся точки

(рис. 2).

Вектор r равен изменению (приращению) радиуса-вектора точки за рассмат-

риваемый интервал времени t .

Рис. 2

7

Длинапути– длинаучасткатраектории S , пройденногоматериальной точкой за данный промежуток времени:

S = S (t) – скалярная функция времени.

При прямолинейном движении вектор перемещения направлен вдоль соответствующего участка траектории и поэтому модуль перемещения| равен пройденному пути r = S . Если все точки траектории лежат в одной плоскости, то движение называется плоским.

Скорость – векторная величина, определяющая быстроту движения в указанном направлении в заданный момент времени.

Средняя скорость – векторная величина, определяемая отношением приращения радиуса-вектора точки к интервалу времени t

r .t

Направления у вектора средней скорости 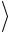и вектора перемещения

Мгновенная скорость – векторная величина, определяемая первой производной радиуса-вектора движущейся точки по времени:

ddtr drdt re .

Вектор мгновенной скорости всегда направлен по касательной к траектории в сторону движения (рис. 3).

Модуль мгновенной скорости –

8

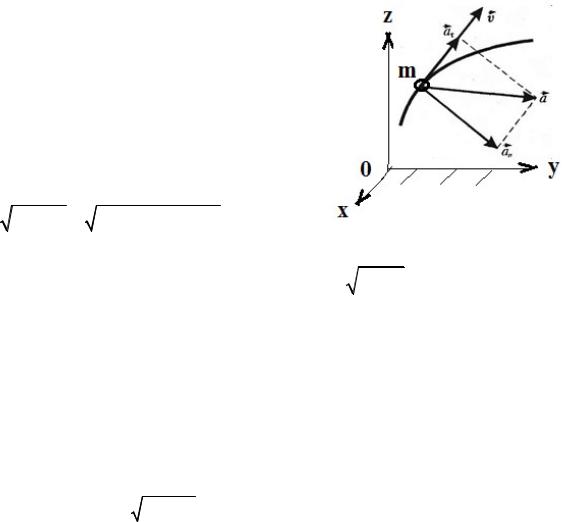
Две составные части ускорения при неравномерном движении по криволинейной траектории:

характеризующая быстроту изменения скорости по направлению

Выводы:

Прямолинейное движение массы m вдоль оси х при постоянном ускорении описывается уравнениями a a x const , an 0 .

Криволинейное движение массы m по окружности при постоянной линейной (тангенциальной) скорости описывается уравнениями const ,

a 0 , a an const .

Криволинейное движение массы m по окружности с постоянным тангенциальным ускорением описывается уравнениями a const

an an ( ,r) 0 , a a2 an2 .

Кинематические уравнения вращательного движения твердого тела

При вращательном движении твердого тела вращается радиус вектор r и все точки теладвижутся по окружностям, центры которых лежат на одной

прямой, называемой осью вращения.

Псевдовекторы d , и – кинематические меры вращательного

движения тел. Точка приложения этих величин может располагаться на оси вращения в любом месте.

9

ющего точку с осью вращения на угол 2 . Поэтому T 2

Вектор и модуль линейной скорости материальной точки тела определяют из уравнений:

шаемых телом при равномерном его движении по окружности, в единицу времени.

n T1 2 .

Угловое ускорение – векторная величина, определяемая первой производной угловой скорости по времени ddt (рис. 6).

10