1958

-прогнозировать пассажирские и автомобильные потоки по уличным, а

также дорожным сетям страны, области, региона либо определенного го-

рода;

-детально анализировать изменения пассажирских/автомобильных пото-

ков при реализации различных решений, связанных с изменением градо-

строительной либо транспортной инфраструктуры;

-формировать оптимальные режимы светофорного регулирования на раз-

личных объектах дорожно-уличной сети.

-выстраивать очередность строительства объектов градостроительной и транспортной инфраструктуры;

-оптимизировать работу городского транспорта.

Вышеперечисленные факторы, а также множество других факторов, оказы-

вают непосредственное влияние на функционирование транспортной системы,

поэтому рассчитать перспективные показатели работы проектируемого и сущест-

вующего объекта стандартными способами невозможно. Проводить эксперимен-

ты с реальной функционирующими транспортными объектами обычно бывает не-

возможно, поскольку это является слишком опасным либо требует существенных финансовых вложений, а результат подобных экспериментов способен оказаться совершенно непредсказуемым. Решить данную проблему позволяет моделирова-

ние транспортной системы, позволяющее протестировать еще не построенные объекты и смоделировать вероятные сценарии их работы, проверив на устойчи-

вость функционирования при различных внештатных ситуациях.

Имитационный метод моделирования используется при моделировании различных транспортно-пересадочных узлов, железнодорожных станций, павиль-

онов метрополитена и прочих объектов современной транспортной инфраструк-

туры. Имитационное микромоделирование позволяет создать максимальным об-

разом приближенную к реальным условиям ситуацию, учесть любые особенности системы и минимизировать финансовые, а также производственные риски.

Имитационные модели позволяют выполнить тестирование еще не постро-

енного объекта, смоделировать разные возможные сценарии его работы, провести

Лист

ВКР-2069059-23.03.01-130636-17 11

ряд экспериментов, связанных с различными внештатными ситуациями, проверив при этом устойчивость работы данного объекта в подобных ситуациях.

К примеру, при моделировании такого транспортно-пересадочного узла, как же-

лезнодорожная станция, учитывается режим работы вокзальных билетных касс,

наличие льготных категорий пассажиров, а также связанные с этим временные особенности оформления проездных документов. Используя имитационное моде-

лирование транспортных потоков, необходимо учитывать проектную нагрузку на отдельные элементы пассажирской инфраструктуры, принимая во внимание не-

равномерность пассажиропотока.

Если для определения пассажиропотока число пассажиров в час разделить на шестьдесят минут, реальная картина сильно исказиться и полученные данные не будут соответствовать действительности, а также тем условиям, в которых функционирует создаваемая инфраструктура. К примеру, на территории вокзала проектируется создание турникетной линейки, которая будет состоять из пятна-

дцати турникетов. Расчетный поток пассажиров на выход составляет пять тысяч человек в час. Если взять средний показатель в минуту, мы получим порядка восьмидесяти пассажиров. Одни пассажир проходит через турникет в среднем за три секунды. Если принимать во внимание такие исходные данные, то получить-

ся, что все пассажиры успеют пройти, и очередей не возникнет. В реальности же ситуация несколько иная. Вышеупомянутые пять тысяч пассажиров прибывают на станцию в четырех электропоездах, которые приходят по расписанию. Если учесть этот факт, а также неравномерное распределение людей по отдельным ва-

гонам, ситуация изменится кардинальным образом. Очереди после прибытия электропоезда на станцию в таком случае будут превышать сорок человек.

Имитационное моделирование ставит своей целью воспроизведение всех деталей движения, включая развитие процесса во времени. При этом усредненные значения потоков и распределение по путям считаются известными и служат ис-

ходными данными для этих моделей. Имитационные модели позволяют оценить скорости движения, задержки на перекрестках, длины и динамику образования

«очередей», или «заторов», и другие характеристики движения. Основная область

Лист

ВКР-2069059-23.03.01-130636-17 12

применения таких моделей совершенствование организации движения, оптимиза-

ция светофорных циклов и др.

Для анализа дорожного движения и транспортных сетей принято выделять три основные группы моделей: прогнозные модели; имитационные модели; опти-

мизационные модели.

Прогнозные модели предназначены для моделирования транспортных пото-

ков в сетях с известной геометрией и характеристиками, при известном размеще-

нии потокообразующих объектов города. При их помощи прогнозируется послед-

ствия в изменении транспортной сети или размещении объектов. Целью прогноза загрузки транспортной сети является расчет усредненных характеристик движе-

ния, таких как объемы межрайонных корреспонденций, распределение участни-

ков движения по путям движения, определение интенсивности движения на от-

дельных участках транспортной сети. Модели этого типа применяются при под-

держке решений в области планирования развития города, для анализа последст-

вий тех или иных мер по организации дорожного движения, выбора альтернатив-

ных проектов развития транспортной сети города.

Имитационное моделирование ставит своей целью воспроизведение всех деталей движения и позволяет определить скорость движения, задержки на пере-

крестках, динамику и длину очередей, другие характеристики движения. Модели данного типа широко применяются при улучшении организации движения.

Прогнозные и имитационные модели дополняют друг друга. Например,

прогноз интенсивности движения служит в качестве исходных данных для имита-

ционного моделирования работы системы координированного управления. В

свою очередь улучшение условий движения приводит к перераспределению транспортных потоков в транспортной сети. Маршрут с лучшими условиями движения привлекает дополнительный объем движения.

Модели прогноза потоков и имитационные модели ставят своей целью аде-

кватное воспроизведение транспортных потоков. По своей сути они являются мо-

делями описания и различаются лишь степенью детализации транспортной сети.

Лист

ВКР-2069059-23.03.01-130636-17 13

Модели оптимизации решают задачи оптимизации маршрутов пассажир-

ских и грузовых перевозок, выбора оптимальной конфигурации сети, расчета оп-

тимальных сигнальных планов работы светофорной сигнализации. При разработ-

ке оптимизационной модели основной задачей является определение целевой функции и установка ограничений. В качестве целевой функции обычно прини-

мают функцию затрат на движение и проводят ее минимизацию. В качестве огра-

ничений выступают требования безопасности движения или обеспечения мини-

мальных потребностей в передвижении.

Все модели транспортных потоков можно разбить на два класса: модели аналоги и модели следования за лидером. В моделях-аналогах движение транс-

портных средств уподобляется какому-либо физическому потоку (гидро– и аэро-

динамические модели). Этот класс моделей принято называть макроскопически-

ми.

В моделях следования за лидером существенно предположение о наличии связи между перемещением ведущего и ведомого автомобиля. По мере развития теории в моделях этой группы учитывалось время реакции водителей, исследова-

лось движение на многополосных дорогах, изучалась устойчивость движения и т.п. Этот класс моделей называют микроскопическими.

Макроскопические или прогнозные модели позволяют симулировать про-

цессы передвижения населения и грузов по городу с выбором путей следования и видов используемого транспорта. Они предназначены для оценок транспортных потоков при изменении транспортной сети, транспортных систем, а также пото-

кообразующих и потокопоглощающих объектов города. В связи с этим основная область их применения – поддержка управленческих решений в области планиро-

вания развития городских территорий, анализ последствий изменений в организа-

ции движения, выбор альтернативных проектов развития транспортной инфра-

структуры и т.п.

Микроскопические или имитационные модели ориентированы на адекват-

ное описание поведения участников транспортного процесса и правильность вос-

произведения параметров и характеристик движения. Имитационные модели по-

Лист

ВКР-2069059-23.03.01-130636-17 14

зволяют оценивать скорости движения, задержки на перекрестках, длину и дина-

мику образования транспортных заторов и т.п. В связи с этим основная область их применения – оценка инженерных решений локальных инфраструктурных проек-

тов, улучшение и оптимизация транспортных потоков в отдельных узлах или группе узлов, подбор светофорных циклов и т.п.

1.2 Микроскопические имитационные модели

Задача вождения в продольном направлении включает действия для дости-

жения желательной скорости и поддержания безопасного расстояния между авто-

мобилями. Решение о смене полосы движения и принятие интервала между сле-

дующими по соседней полосе автомобилями для совершения маневра перестрое-

ния, является задачей поперечного вождения. Обе задачи могут быть описаны от-

носительно состояния окружающей среды, транспортного потока или с учетом других автомобилей в транспортном потоке.

Продольное поведение водителя может быть классифицировано следующим образом:

–поведение в условиях свободного потока;

–поведение следования за лидером;

–поведение в условиях «остановка – движение».

В условиях свободного потока плотность очень низка, и среднее расстояние движения является большим. Таким образом, транспортные средства могут дви-

гаться со своей желаемой скоростью. Поскольку плотность начинает увеличи-

ваться из-за увеличивающегося спроса, транспортные средства начинают двигать-

ся на более близких расстояниях, чтобы максимизировать емкость полосы движе-

ния. Индивидуальные транспортные средства вынуждены следовать друг за дру-

гом с уменьшенной скоростью. Как только достигается критическая плотность

(при которой емкость полосы движения используется максимально), тогда движе-

ние автомобилей переходит в режим «остановка – движение». Это поведение транспортного потока соответствует правой части основной диаграммы транс-

портного потока.

Лист

ВКР-2069059-23.03.01-130636-17 15

Модели смены полосы движения описывают процесс принятия решения во-

дителями о выполнении маневра смены полосы движения, который может быть рассмотрен как последовательность трех шагов:

–принятие решения о смене полосы движения;

–выбор целевой полосы движения;

–принятие интервала для совершения маневра.

Рассмотрим модели принятия решения о смене полосы движения. В 1980-

ых, Гиппс представил модель, которая рассматривала решение о смене полосы движения как возможный, необходимый или желательный механизм. Данная мо-

дель предполагает, что любая смена полосы возможна только в том случае, если у целевой полосы движения имеется интервал, который превышает или равен тре-

буемому. Это предположение могло быть приемлемым, когда смена полосы дви-

жения – желательное действие. Но если маневр – вынужденное изменение полосы движения, и безопасный интервал меньше, чем необходимый, как например, в на-

сыщенных состояниях транспортного потока, то это предположение недопустимо.

П. Хидас предложил вариант модели Гиппса, которая рассматривает смену полосы движения как ненужное, необходимое или желательное. Если изменение полосы движения рассматривается как необходимое решение (как в случае окон-

чания полосы движения), то смена полосы движения выполняется без дальней-

ших последствий.

Подход, подобный модели П. Хидаса, был предложен в работе Я. Янга и Х.

Н. Коутсопоулоса. Модель классифицирует решение о смене полосы движения как принудительное или контролируемое. Контролируемое решение о смене по-

лосы движения происходит, когда скорость впереди идущего автомобиля ниже желательной скорости. Принудительное решение о смене полосы движения про-

исходит, когда автомобиль хочет объехать расположенное по ходу движения пре-

пятствие, реакция на предписание о направлениях движения по полосам движе-

ния, достижение следующей связи, и т.д.

Подобие между моделями П. Хидаса и Я. Янга состоит в том, что обе моде-

ли используют функцию приоритета для принудительной смены полосы движе-

Лист

ВКР-2069059-23.03.01-130636-17 16

ния. Модели задают вероятность предоставления приоритета для автомобиля, ко-

торый нуждается в принудительной смене полосы движения. Согласно данной функции, водитель на соседней полосе движения замедляется, чтобы обеспечить интервал, который позволяет автомобилю произвести смену полосы движения.

Норма замедления автомобиля на целевой полосе определена с использованием модели следования за лидером.

Т. Толедо представил модель, которая позволяет водителю выбирать целе-

вую полосу движения и приемлемый интервал, при этом целевой полосой движе-

ния необязательно должен быть смежный переулок. Для достижения целевой по-

лосы с приемлемым интервалом, водитель должен будет ускориться, замедлиться или сменить полосу движения. Модель использует ряд logit – уравнений для оп-

ределения привлекательности каждой полосы движения. Привлекательность по-

лосы движения означает удовлетворение требований водителя по показателям безопасности, степени свободы выполнить маневр, скорости по полосе движения,

и т.д.

Влюбой из приведенных моделей смена полосы движения возможна только

втом случае, если у целевой полосы имеется интервал, больший или равный не-

обходимому для выполнения маневра.

Модели принятия интервалов. Приняв решение о смене полосы движения,

водитель должен выбрать момент для совершения маневра. Предполагается, что для каждого водителя существует собственный критический интервал. Интервалы между автомобилями на смежной полосе, которые меньше критического откло-

няются, а интервалы, превышающие критический, принимаются водителями, и

производится смена полосы движения.

Различные водители обладают различным поведением в оценке и принятии интервалов. Кроме того, водители могут вести себя по-разному в одной и той же ситуации. Эта неоднородность поведения водителей имеет тенденцию к стохас-

тичному распределению. На основе гипотез о законах распределения критических интервалов было предложено множество различных моделей.

Лист

ВКР-2069059-23.03.01-130636-17 17

Р. Херман, Г. Х. Вэйс предложили модель, которая предполагает распреде-

ление критических интервалов по экспоненциальному распределению, Д. Р. Дрю в свой модели использовал логнормальное распределение. Недостатком данных моделей является тот факт, что не учитывался эффект ранее отклоненных интер-

валов.

В 1960-ых Г. Х. Вэйс и А. Марадудин получили функцию α(tgap), которая описывает вероятность принятия водителем определенной продолжительности интервала tgap и начала маневра смены полосы движения. Данная функция приме-

нима только в том случае, если у водителя имеется хотя бы одно наблюдение, то есть один принятый или отклоненный интервал. Даганзо предложил формулиров-

ку probit model, для оценки принятия интервалов для каждого индивидуального водителя. Эта модель использует полную историю отклоненных и принятых ин-

тервалов.

1.3 Микроскопическая модель SUMO

«Simulation of Urban MObility» (SUMO) программа микроскопического мо-

делирования дорожного движения с открытым кодом (лицензия GPL), разрабо-

танная в Институте транспортных систем немецкого аэрокосмического центра

(Institute of Transportation Systems at the German Aerospace Center) в 2000 году. Ос-

новной задачей разработки программы стала поддержка сообщества исследовате-

лей транспортного потока инструментом, в котором могли бы реализовать и про-

вести оценку собственные алгоритмов. Основное назначение программы состоит в оценке методов организации дорожного движения, таких как новые системы управления светофорными объектами или новые подходы к управлению транс-

портными потоками.

SUMO включает среду моделирования и пакет программ, необходимых для подготовки модели. При разработке программы была поставлена задача повыше-

ния скорости моделирования и кросс платформенность приложения (в настоящее время доступны версии для операционных систем Windows, Linux и MacOS). Са-

мые первые версии программы были разработаны с управлением из командной

Лист

ВКР-2069059-23.03.01-130636-17 18

строки - первоначально отсутствовал какой-либо графический интерфейс и все параметры должны были устанавливаться вручную. Это должно было увеличить скорость моделирования за счет отказа от медленного процесса визуализации.

Позже была добавлена графическая среда для визуализации процесса моделиро-

вания.

SUMO является уникальной программой по скорости выполнения и воз-

можностям управления процессом моделирования, однако управление из команд-

ной строки делает использование SUMO несколько неудобным по сравнению с другими пакетами моделирования.

В программе SUMO используется модель С. Краусса. Она основана на на-

личии безопасного интервала между ведомым транспортным средством и лиде-

ром, необходимым для безопасной остановки. Используя приближенную формулу для тормозного пути

d (v) = v€2 / (2b), (1.1)

учитывая максимальное замедление взаимодействующих транспортных средств (предполагается, что замедления равны) и время реакции водителя ведо-

мого автомобиля, можно получить следующую зависимость для определения безопасной скорости.

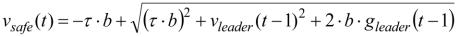, (1.2)

где vsafe(t) – безопасная скорость в момент времени t (м/с);

τ – время реакции водителя ведомого автомобиля (c); b – максимальное замедление (м/с2);

vleader(t) – скорость лидера во время t (м/с);

gleader(t) – дистанция между передней частью ведомого автомобиля и задним бампером лидера во время t (м).

Модель учитывает расстояние до лидера, его скорость и гарантирует дви-

жение без столкновения. Для того, чтобы гарантировать адекватные значения ус-

корения и скорости необходимо наложить ограничения на значения «желаемой» скорости:

Лист

ВКР-2069059-23.03.01-130636-17 19

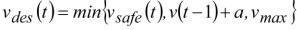, (1.3)

где vdes(t) – желаемая скорость (м/с); v(t) – текущая скорость (м/с);

a – максимальное ускорение (м/с2);

vmax – максимальная скорость автомобиля, м/с.

Одним из основных преимуществ модели Краусса является предположение,

что водитель не собирается развивать желаемую скорость. Фактическая скорость на самом деле несколько меньше желаемой, что повышает качество модели. На-

пример, случайное отличие от желаемой (оптимальной) скорости приводит к спонтанному образованию заторов и медленному старту автомобилей, характер-

ному для реальных водителей. Модель реализует эту особенность поведения во-

дителей стохастическим замедлением. Для этого на очередном шаге моделирова-

ния скорость транспортного средства вычисляется как:

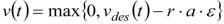, (1.4)

где r – случайное число между 0 и 1;

ε – индивидуальность (несовершенство) водителя автомобиля, принимаю-

щее значение между 0 и 1;

v(t) – конечная (финальная) скорость автомобиля в момент времени t, м/с.

При разработке программы SUMO в исходную модель Краусса были внесе-

ны два изменения. Первое заключается в использовании линейной функции уско-

рения, обеспечивающей его уменьшение с ростом скорости:

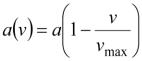. (1.5)

Второе изменение заключается в уменьшении индивидуальности (несовер-

шенства) водителей при разгоне на малых скоростях:

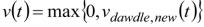, (1.6)

где

. (1.7)

Лист

ВКР-2069059-23.03.01-130636-17 20