1903

метр, эффект i-го уровня дискретного фактора; ij – случайная ошибка j-го

наблюдения на i-м уровне фактора.

Модель типа (4.6) для дискретных переменных имеет особенности:

отсутствие достаточности степеней свободы для оценки всех параметров. Это приводит к дополнительным ограничениям параметров. При

2

i 0 единственные оценки параметров получаются по методу наи-

i 1

меньших квадратов. Раздел математической статистики, который называется дисперсным анализом, строится на моделях подобного типа. При обработке результатов наблюдений сначала проверяется гипотеза о равенстве нулю влияния изменения всех уровней данного фактора, то есть о равенство нулю величин α1, α2,…. αs. Тесты для проверки гипотез в дисперсном анализе совместно рассматривают и оптимальность плана и оптимальность теста;

превращение в комбинаторную задачу построения плана, в отличие от случая непрерывных переменных, так как план строится на многомерной решётке, которая определяется числом уровней каждого фактора и членами, входящими в модель. В тоже время план, построенный для дискретных переменных, может быть использован и для модели с непрерывными переменными.

Обработка результатов наблюдений методом дисперсионного анализа предусматривает оценку дисперсий, определяющих рассеяние, связанное с ошибкой эксперимента, межблоковое рассеяние и рассеяние, определяемое эффектом изменения вариантов испытания.

В дисперсионном анализе определяется две дисперсии: первая из них служит оценкой для рассеяния, задаваемого ошибкой опыта S12 2 , а вторая задается рассеянием изучаемых факторов. В простейшем случае S22 2 n 2 T , , где Т – изучаемый фактор, п – число параллельных

определений. С помощью дисперсионного отношения F f2 , f1 S2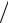2 S12

проверяется нуль-гипотеза 2 T 0 .

Если фактор Т варьируется на k уровнях и на каждом уровне делается n параллельных опытов, то возникает необходимость в сравнении диспер-

251

Рассеяние между средними задается только ошибкой опыта, при принятии нуль-гипотезы H0;22 12 с 2 T 0 . В формуле для вычисления S12

и S22 заданы две независимые оценки 2 , при постоянном факторе Т.

При существовании различия в средних значениях для разных испытаний они распределяются по столбцам с ранжировкой по величине, с установлением между какими средними существует значимое различие. После анализа дисперсий переходят к индивидуальным сравнениям всех средних между собой с помощью критерия Дункана [130].

Статистический анализ уравнения регрессии проводится после вычисления коэффициентов регрессии и проверки их значимости. Проверка гипотезы об адекватности данного уравнения линейному уравнению позволяет установить полученное соответствие изучаемому явлению или заменить его более сложной моделью. Количественной оценкой адекватности уравнения регрессии является дисперсия неадекватности. Она характеризует квадрат отклонений экспериментальных значений (у) от теорети-

ческих. Дисперсия неадекватности Sад2 является количественным показателем адекватности уравнения:

N 2

Sад2 уп расч уп эксп N k 1 , (4.8) n 1

где уп расч – значение параметра оптимизации в n-м опыте, предсказанное уравнением регрессии; уп эксп – значение параметра в том же опыте, опре-

деленное экспериментально; N – число степеней свободы при определении дисперсии неадекватности, т.е. число опытов в матрице планирования; k – число факторов.

Гипотеза об адекватности проверяется с помощью критерия Фишера (F-критерия):

Гипотеза об адекватности линейной модели принимается, если расчетное значение F-критерия F расч не превышает его табличного значения

F табл , которое принимается для выбранного уровня значимости. Она

может использоваться для последующих этапов планирования, в частности для поиска направления движения по градиенту к оптимуму. В противном случае уравнение регрессии дополняется членами более высокого порядка.

252

Другой способ проверки адекватности линейного уравнения предусматривает оценку результата опыта на основном уровне по свободному члену уравнения регрессии b0, когда все остальные факторы исключены. С помощью сравнения результата опыта с величиной свободного члена проверяется гипотеза о равенстве нулю суммы коэффициентов при квадратичных членах (ноль-гипотеза). Ноль-гипотеза принимается, если разность b0 y0 не превышает среднеквадратичной ошибки эксперимента. Значи-

мость этого различия проверяется сопоставлением с критерием Стьюдента:

серий опытов.

Для проверки однородности выборочных дисперсий Su2 регрессион-

ного анализа используется критерий Кохрена [127].

Различается стратегическое и тактическое планирование эксперимента. Стратегическое планирование эксперимента связано с установлением зависимостей переменных отклика от контролируемых в процессе эксперимента факторов, которые оптимизируют переменную отклика.

Стратегическое планирование учитывает ряд особенностей, влияющих на результаты моделирования. К ним относятся построение рационального плана эксперимента, наличие необходимого количества факторов, многокомпонентный характер функции отклика, стохастическая сходимость результатов моделирования и ограниченность ресурсов на проведение эксперимента.

Отбор факторов, наиболее существенно влияет на результаты моделирования. Так, полный факторный эксперимент при варьировании факторов на двух уровнях при наличии 10 факторов требует проведения 1024 опыта. Вместе с тем большинство технических систем работают в соответствии с принципом Парето, который устанавливает, что в большинстве систем

253

20 % факторов определяет 80 % свойств системы, а остальные 80 % факторов определяют лишь 20 % ее свойств [130]

Стратегическое планирование экспериментов выделяет два этапа – построение структурной модели и построение функциональной модели. Структурная модель выбирается исходя из того, что должно быть сделано, а функциональная – из того, что может быть сделано. Структурная модель формирует число факторов и число уровней для каждого фактора. Функциональная модель плана эксперимента обосновывает необходимое количество информационных точек с определением количества элементов структурной модели.

Тактическое планирование назначает размер выборки, определяет начальные условия эксперимента и уменьшает дисперсию для увеличения точности оценки результатов. При стохастическом моделировании неточность результата эксперимента в значительной мере определяется размером выборки из-за случайного характера этих значений. Размер выборки определяется либо независимо от работы модели, либо в процессе моделирования на основе полученных с помощью модели соответствующих результатов. Необходимость априорного анализа возникает в случаях наличия общих оснований для принятия того или иного закона распределения случайной величины. Например, суммы большого числа независимых случайных величин (нормальное распределение) или редкие события (распределение Пуассона).

Для предварительной оценки параметров распределения проводится пробный эксперимент. При известном законе распределения объем выборки находится по правилам математической статистики в зависимости от заданной надежности (обеспеченности). Так, для нормального распределения имеет место зависимость [130]:

где t – коэффициенты зависящие от количества измерений и заданной доверительной вероятности (коэффициенты Стьюдента); – расстояние до границ доверительного интервала (точность оценки); – среднеквадратическое отклонение.

При неизвестном законе распределения и в случае отсутствия основания для принятия нормального закона, рекомендуется использовать неравенство Чебышева, устанавливающего верхнюю границу для вероятности отклонения случайной величины от её математического ожидания ( )

[130, 372]:

При желательной оценке попадания среднеарифметических наблюдаемых значений mx'* в интервал, равный mx 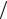4 с вероятностью 0,95, спра-

254

ведливо выражение P m*x mx 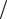4 , где mx – математическое ожидание.

ность разности средних арифметических и математических значений со-

ный размер выборки для указанной обеспеченности существенно больше, чем для нормального распределения. При данных условиях для нормального распределения он равен 61. Однако использование неравенства Чебышева позволяет получить гарантированную статистическую точность «с запасом».

При проверке близости распределений откликов модели и реальной моделируемой системы или сравнения распределения откликов на двух режимах работы системы объем выборки предлагается определять по формулам [130]:

При неизвестном стандартном отклонении грубая оценка величины σ получается из условия, что размах переменной отклика равен примерно 4σ [130].

Использование методов уменьшения дисперсии значительно увеличивает эффективность моделирования. Методы уменьшения дисперсии применяются:

для увеличения точности при работе с выборкой постоянного объема;

для уменьшения объема выборки при обеспечении постоянной степени точности.

Метод стратифицированных выборок определяет разбивку всей выборки на ряд выборок меньшего объема (страт). Вследствие более однородности элементы в каждой страте обладают меньшей дисперсией, чем элементы всей совокупности в целом. Размеры страт выбираются различными способами, например, разбивкой совокупности на страты с одинаковым числом элементов или при наличии априорной информации – выбором страты с одинаковыми дисперсиями. Обоснованием числа выборочных значений внутри каждой страты служит дисперсия внутри страты.

255

Метод определения выборки по значимости позволяет определить выборочные значения переменной с помощью умножения на специально подобранный весовой коэффициент для компенсации ошибки. Частным случаем выборки по значимости является метод, называемый в зарубежной литературе «Русской рулеткой» [130].

Планирование экспериментов с имитационными моделями реализуется методами статистического моделирования. При этом возникает проблема стохастической сходимости результатов машинного эксперимента. Метод компенсации предназначен для систем имитационного моделирования. Он используется при оценке х1 и х2 неизвестного параметра у, имеющего отрицательную корреляцию с х2. При выборе окончательной оценки для (х1+х2)/2 параметра у этот метод имеет существенно меньшую дисперсию [130]:

4.3.Критерии оптимальности планов

ипланирование факторных экспериментов

При формализации изучаемого явления в математическую модель задача эксперимента сводится к статистической оценке параметров модели. Эти требования называются критериями оптимальности плана эксперимента.

Планирование считается оптимальным, если оно позволяет получать независимые оценки коэффициентов регрессии, определяемые с одинаковой дисперсией. Перечисленным условиям отвечает планирование, обладающее свойствами ортогональности и рототабельности.

Все статистические критерии разделяются на две большие группы. К первой группе относятся критерии, связанные с точностью оценок параметров, ко второй – критерии и свойства планов, связанные с ошибкой в оценке модели.

К критериям первой группы относятся: D – оптимальность, А – оптимальность, Е – оптимальность и ортогональность. Наглядным геометрическим истолкованием точности оценок параметров являются их эллипсоид рассеяния [417].

Эллипсоид рассеяния оценок параметров для D-оптимального плана имеет минимальный объём, методы построения которых приведены в работе [739].

Планам, отвечающим критерию А соответствует эллипсоид рассеяния с наименьшей суммой квадратов длин осей. Этот критерий справедлив для планов с минимальной средней дисперсией оценок коэффициентов или с наименьшим значением следа ковариационной матрицы.

256

Критерий Е-оптимальности не допускает, чтобы отдельные оценки параметров имели слишком большие дисперсии и ковариации.

План называется ортогональным, если ему соответствует диагональная ковариационная (информационная) матрица оценок. Для ортогональных планов все оценки параметров независимы. Рототабельность плана представляет свойство плана, при котором дисперсия оценки функции отклика зависит только от расстояния от центра плана. Рототабельность показывает, что информация, содержащаяся в уравнении регрессии, равномерно «размазана» по гиперсфере относительно центра эксперимента, а предсказанные значения параметра оптимизации имеют минимальные дисперсии в различных точках факторного пространства. Дисперсия оценки модели зависит только от длины радиуса, проведённого из центра эксперимента, но не от угла, под которым этот радиус проведён.Эти дисперсии на одинаковых расстояниях от центра эксперимента равны между собой. Принимая за меру информации величину 1/σ2, информация, содержащаяся в уравнении регрессии, будет равномерно содержаться в сферической области с радиусом определённой величины.

Необходимость выбора планирования эксперимента, при котором количество информации, содержащейся в уравнении регрессии было бы одинаково для всех эквидистантных точек, является целью исследователя, который не знает заранее определенную область факторного пространства, где находится интересующий его участок экспериментального исследования. Однако, условиям ортогональности и рототабельности одновременно удовлетворяют только планы первого порядка.

Ко второй группе относятся критерии требования и свойства планов, связанных с ошибкой в оценке модели. Это – критерии G-оптимальности, Q-оптимальности, рототабельности, максимальной точности оценки координат экстремума, униформности, минимизации среднеквадратической систематической и случайной ошибки, оптимальности планирования для проверки гипотезы о неадекватности модели и рандомизация. Критерии предъявляют требования: насыщенности, композиционности и простоты обработки [417, 688].

Критерий G-оптимальности планов минимизирует на множестве планов максимальное значение дисперсии оценки модели. Применение G-оп- тимального плана гарантирует не допущение в области планирования точек со слишком низкой точностью оценки поверхности отклика.

В Q-оптимальных планах минимизируется средняя дисперсия оценки модели. В рототабельном плане дисперсия оценки модели представляется в виде функции рассеяния до центра эксперимента. Это делает любое направление от центра эксперимента равнозначным по точности оценки поверхности отклика. Для рототабельного плана информационные контуры плана поверхности с равными значениями дисперсии оценки модели

257

представляются в виде сферы. Ортогональность показывает, что все факторы расположены симметрично относительно центра эксперимента и коэффициенты регрессии оцениваются с минимальной дисперсией [417].

Критерий максимальной точности оценки координат экстремума необходим для построения планов, минимизирующих дисперсию оценки поверхности отклика в области экстремума. Он определяет предварительную грубую оценку его положения.

Критерий униформности требует, чтобы дисперсия оценки модели в некоторой области вокруг центра эксперимента была постоянной. Использование метода минимизации среднеквадратической систематической и случайной ошибки позволяет получить в эксперименте минимизацию общего, случайного и систематического среднеквадратического отклонения оценки выборной модели от истинной [417, 536].

Критерий «оптимальность планирования для проверки гипотезы о неадекватности модели» применяется в случае планирования в эксперименте сложной модели. Для её проверки используется гипотеза о неадекватности модели [417].

Рандомизация обязывает проведение измерений в случайном порядке. Рандомизация проводится как для исключения влияния переменных, неконтролируемым образом изменяющихся во времени, так и для исключения влияния переменных, изменяющихся неконтролируемым образом в пространстве (неоднородность материала). Рандомизация исследований исключает влияние систематических ошибок, вызванных внешними условиями.

Требование насыщенности определяет минимальное число измерений в плане. При числе измерений равном числу неизвестных оцениваемых параметров, план называется насыщенным. В тоже время, использование планов с меньшим числом измерений не позволяет определить единственные оценки всех параметров.

Требование композиционности позволяет разделить эксперимент на несколько этапов с постепенным переходом от простых моделей к более сложным, используя предыдущие наблюдения. Примером является модель эксперимента «крутого восхождения». На первом этапе эксперимента даётся оценка коэффициентов полинома первого порядка, на втором – коэффициентом полиноминальной модели второго порядка.

Методологической основой проведения экспериментальных исследований с учётом привлечения математической статистики является:

1)оптимальноеиспользованиепространстванезависимыхпеременных;

2)последовательность эксперимента;

3)рандомизация;

4)репродукция (свёртка) информации.

258

В технике применяются два основных плана проведения экспериментов: последовательный(классический) и случайный (рандомизированный).

Основой последовательного плана является постоянство всех независимых переменных, кроме одной. Этот план применяется в ситуациях, когда каждое наблюдение является либо очень дорогим, либо труднодоступным. По существу классический многофакторный эксперимент представляет последовательность однофакторных экспериментов, позволяющий находить такие простые функции, как [649]:

Последовательный план эксперимента может быть как сбалансированным, так и не сбалансированным, в зависимости от числа уровней для переменной X по сравнению с переменной Y. Он применяется абсолютно во всех областях.

Эксперименты, связанные с испытаниями строительных материалов, являются невоспроизводимыми. Они проводятся во времени необратимо без возможности их изменения или повторения. Последовательный план применяется при проведении испытаний отдельных строительных материалов, в процессе которых происходят непрерывные изменения или наблюдается ухудшение характеристик, а также в частных случаях, например, когда последовательность получения данных является параметром эксперимента.

Концепция последовательного эксперимента оказала большое влияние на развитие статистических методов исследования, особенно в задачах планирования так называемых экстремальных экспериментов [130]. Содержанием концепции является использование последовательной пошаговой стратегии принятия решений в зависимости от результатов, полученных на отдельных этапах исследования. Инструментом действия стратегии являются различные методы: линейное приближение, движение по градиенту линейного приближения и описание полиномами второго и третьего порядка.

Математической основой оптимального использования пространства независимых переменных является математическая статистика. Концепция оптимального использования пространства независимых переменных обосновывает условия применения многофакторного эксперимента. С общеметодологических позиций использование статистических методов в планировании эксперимента позволяет рассматривать изучаемые факторы как случайные величины. При этом решающим обстоятельством оказывается

259

не физическая природа фактора, а постановка задачи и условие проведения эксперимента.

Схема эксперимента называется многофакторной, когда в процессе эксперимента оперируют всеми факторами. Факторный план находит гораздо менее широкое применение, хотя по времени он короче и всегда точнее, чем классический [649]. Основное преимущество факторных экспериментов состоит в том, что для каждой кривой используется вся совокупность данных и поэтому точность результатов является максимальной. При факторном планировании значения входных переменных одновременно комбинируются в разных вариантах в отличие от классического эксперимента, в котором влияние этих значений на результаты исследования рассматривается по одному.

Эффект математической статистики в многофакторном эксперименте оценивается по совокупности всех опытов. По сравнению с дисперсией единичного измерения данная дисперсия оценки результатов эксперимента уменьшается в k 1 n раз, так как статистическая оценка будет происхо-

дить во всех k 1 n опытах. Здесь k – независимые переменные (факто-

ры), а n – повторные опыты [418]. Это даёт более точные оценки неизвестных параметров регрессии при равном числе измерений. Многофакторный эксперимент повышает эффективность эксперимента в задачах с большим числом независимых переменных.

Комбинация факторов, влияющих на проведение эксперимента, называется уровнем факторов. По числу факторов k определяется число опытов N, необходимое для реализации всех возможных сочетаний уровней

факторов: N pk , где р – число уровней. В теории планирования экспери-

мента под понятием степеней свободы понимается разность между числом опытов и числом коэффициентов, которые уже вычислены по результатам этих опытов независимо друг от друга. Например, при полном факторном

эксперименте, когда число опытов N pk 23 , число степеней свободы

будет N–k–1=8–3–1=4.

Эксперимент, реализующий все возможные сочетания уровней факторов, называется полным факторным экспериментом. В полном факторном эксперименте между моделями регрессионного анализа и теми моделями дисперсионного анализа, где переменным приписываются фиксированные уровни существует глубокая связь. Дисперсионный анализ рассматривается как частный случай регрессионного, когда областью независимых переменных является конечное множество точек.

Рандомизация рассматривается как приём планирования эксперимента, исходя из какой-либо одной статистической концепции, например, минимизации дисперсии полученных результатов. Она является одним из приё-

260