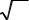1903
.pdf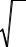
9) осуществляется проверка линии регрессии с помощью критерия
линейности 2 r3 и его основной ошибки |
s |
|
, где |
2 – корре- |
|
|
|
n |
|
|
|
|
|
ляционное отношение Пирсона 2 y 2 , n – число испытанных образцов. my
Линейность подтверждается при значении ξ, не превышающей свою основную ошибку s .
Анализ вероятностного рассеяния характеристик выносливости при статистической обработки результатов испытаний металлических конструкций имеет следующую последовательность [35]:
1)составляется вариационный ряд числа циклов нагружения в порядке возрастания значений долговечности Ni ;
2)при количестве опытных образцов n > 20 штук, накопленные частоты Pi подсчитываются по формуле:
P PВ 0,5 100% , |
(3.59) |
i n
где PB – значение выборочной вероятности в вариационном ряду; n – коли-
чество образцов в выборке.
При количестве образцов в выборке n ≤ 20 значение Pi принимается по табл. 3.10 [35].
3)определяется логарифм долговечности X lg N ;
4)результаты испытаний в виде точек с координатами Pi lg Ni пред-
ставляются в нормально логарифмическом масштабе. При образовании экспериментальными точками прямой линии статистические исследования продолжаются в ниже следующим порядке:
5) определяется среднее арифметическое логарифмов долговечностей по формуле:
|
|
iN1lg Ni |
. |
(3.60) |
|
lg N i |
|||||
n |
|||||
|
|
|
|
||
6) |
вычисляются все частные отклонения долговечности от среднего |
|||
арифметического значения: |
|
|||
|
lg N lg Ni |
|
. |
(3.61) |
|
lg N |
|||
7) |
определяется сумма квадратов частных отклонений |
|
||
|
n |
|
||
|
lg2 . |
(3.62) |
||
i 1
241

Таблица 3 . 1 0
Значение выборочной вероятности Р для выборок малого объёма (n<20)
i |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
1 |
0.5000 |
0,2929 |
0,2063 |
0,1591 |
0,1294 |
0,1091 |
0,0943 |
0,0830 |
0,0741 |
0,0670 |
0,0611 |
0,0561 |
0,0519 |
0,0483 |
0,0452 |
0,0424 |
0,0400 |
0,0378 |
0,0358 |
0,0341 |
2 |
|
0.7071 |
0,5000 |
0,3864 |
0,3147 |
0,2655 |
0,2295 |
0,2021 |
0,1806 |
0,1632 |
0,1489 |
0,1368 |
0,1266 |
0,1178 |
0,1101 |
0,1034 |
0,0975 |
0,0922 |
0,0874 |
0,0831 |
3 |
|
|
0,7937 |
0,6136 |
0,5000 |
0,4218 |
0,3648 |
0,3213 |
0,2871 |
0,2694 |
0,2366 |
0,2175 |
0,2013 |
0,1873 |
0,1751 |
0,1644 |
0,1550 |
0,1465 |
0,1390 |
0,1322 |
4 |
|
|
|
0,8409 |
0,6853 |
0,5782 |
0,5000 |
0,4404 |
0,3935 |
0,3557 |
0,3244 |
0,2982 |
0,2760 |
0,2568 |
0,2401 |
0,2254 |
0,2125 |
0,2009 |
0,1905 |
0,1812 |
5 |
|
|
|
|
0,8706 |
0,7345 |
0,6352 |
0,5596 |
0,5000 |
0,4519 |
0,4122 |
0,3789 |
0,3506 |
0,3265 |
0,3051 |
0,2865 |
0,2700 |
0,2553 |
0,2421 |
0,2302 |
6 |
|
|
|
|
|
0,8909 |
0,7706 |
0,6787 |
0,6065 |
0,5481 |
0,5000 |
0,4596 |
0,4253 |
0,3958 |
0,3700 |
0,3475 |
0,3275 |
0,3097 |
0,2937 |
0,2793 |
7 |
|
|
|
|
|
|
0,9057 |
0,7979 |
0,7129 |
0,6443 |
0,5878 |
0,5404 |
0,5000 |
0,4653 |
0,4350 |
0,4085 |
0,3850 |
0,3641 |
0,3453 |
0,3283 |
8 |
|
|
|
|
|
|
|
0,9170 |
0,8194 |
0,7406 |
0,6756 |
0,6211 |
0,5747 |
0,5347 |
0,5000 |
0,4695 |
0,4425 |
0,4184 |
0,3968 |
0,3774 |
9 |
|
|
|
|
|
|
|
|
0,9259 |
0,8368 |
0,7634 |
0,7018 |
0,6494 |
0,6042 |
0,5650 |
0,5305 |
0,5000 |
0,4728 |
0,4484 |
0,4264 |
10 |
|
|
|
|
|
|
|
|
|
0,9330 |
0,8511 |
0,7825 |
0,7240 |
0,6737 |
0,6300 |
0,5915 |
0,5575 |
0,5272 |
0,5000 |
0,4755 |
11 |
|
|
|
|
|
|
|
|
|
|
0,9389 |
0,8632 |
0,7987 |
0,7432 |
0,6949 |
0,6525 |
0,6150 |
0,5816 |
0,5516 |
0,5245 |
12 |
|
|
|
|
|
|
|
|
|
|
|
0,9439 |
0,8734 |
0,8125 |
0,7599 |
0,7135 |
0,6725 |
0,6359 |
0,6032 |
0,5736 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
0,9481 |
0,8822 |
0,8249 |
0,7746 |
0,7300 |
0,6903 |
0,6547 |
0,6226 |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,9517 |
0,8899 |
0,8356 |
0,7875 |
0,7447 |
0,7063 |
0,6717 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,9548 |
0,8966 |
0,8450 |
0,7991 |
0,7579 |
0,7207 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,9576 |
0,9025 |
0,8535 |
0,8095 |
0,7698 |
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,9600 |
0,9078 |
0,8610 |
0,8188 |
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,9622 |
0,9126 |
0,8678 |
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,9642 |
0,9169 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,9659 |
242

8) вычисляется дисперсия
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
lg2 |
|
|
|
|
|
|
||||||
|
|
|
S |
i 2 |
|
|
|
; |
|
|
|
|
(3.63) |
|||||
|
|
|
n 1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9) среднее квадратичное отклонение имеет вид: |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 ; |
|
|
|
|
|
(3.64) |
||
|
|
|
|
|
S |
S |
|
|
|
|
|
|||||||
10) определяются доверительные пределы для математического ожи- |
||||||||||||||||||
дания с заданной доверительной вероятностью γ по формуле: |
|
|||||||||||||||||
|
|
|
s |
|
|
|
s |
tq,k , |
(3.65) |
|||||||||
|
lg N |
|||||||||||||||||
|
tq,k lg N |
|||||||||||||||||
|
|
n |
||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||
где α – математическое ожидание случайной величины lg N ; tq,k |
– коэффи- |
|||||||||||||||||
циент определяемый по табл. 3.11 [35] в зависимости от q 1 100% и k n 1, где – доверительная вероятность; n – количество образцов в
выборке; 11) вычисляются доверительные интервалы для среднего квадратич-
ного отклонения σ с заданной доверительной вероятностью γ, обычно принимаемой равной 90 %, 95 % по формуле:
z |
|
n 1 |
z |
|
n 1, |
(3.66) |
S |
S |
|||||
1 |
|
n |
2 |
|
n |
|
|
|
|
|
|
где n – количество образцов в выборке; z1, z2 – коэффициенты, опре-
деляемые по табл. 3.12 в зависимости от доверительной вероятности γ и числа образцов в выборке;
12) определяется коэффициент вариации:
|
|
|
|
|
|
|
|
|
v |
S |
|
; |
(3.67) |
||||
|
|
|
|
|
||||
lg N |
||||||||
|
|
|
|
|||||
13) в нормально-логарифмическом масштабе вычерчиваются график распределения долговечности в виде прямой, проходящей через две точки,
с координатами одной точки Р=50 %, lg N lg N и другой, определяемой
выбором вероятности разрушения, 100 % > Р > 50 %. Расчёт долговечности при этой вероятности производится по формуле:
lg N |
lg N |
U p |
|
, |
(3.68) |
S |
где квантиль U p определяется по табл. 3.13;
243

Таблица 3 . 1 1 Коэффициенты tq.k для расчёта доверительных интервалов математического ожидания в зависимости от q и k
q |
10,0 |
5,0 |
2,5 |
2,0 |
1,0 |
0,5 |
0,3 |
0,2 |
0,1 |
k |
|
12,706 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
6,314 |
25,452 |
31,821 |
63,657 |
127,300 |
212,200 |
318,300 |
636,600 |
|
2 |
2,920 |
4,303 |
6,205 |
6,965 |
9,925 |
14,089 |
18,216 |
22,327 |
31,600 |
3 |
2,353 |
3,182 |
4,177 |
4,541 |
5,841 |
7,453 |
8,891 |
10,214 |
12,922 |
4 |
2,132 |
2,776 |
3,495 |
3,747 |
4,604 |
5,597 |
6,435 |
7,173 |
8,610 |
5 |
2,015 |
2,571 |
3,163 |
3,365 |
4,032 |
4,773 |
5,376 |
5,893 |
6,869 |
6 |
1,943 |
2,447 |
2,969 |
3,143 |
3,707 |
4,317 |
4,800 |
5,208 |
5,956 |
7 |
1,895 |
2,365 |
2,841 |
2,998 |
3,499 |
4,029 |
4,442 |
4,785 |
5,408 |
8 |
1,860 |
2,306 |
2,752 |
2,896 |
3,355 |
3,833 |
4,199 |
4,501 |
5,041 |
9 |
1,833 |
2,262 |
2,685 |
2,821 |
3,250 |
3,690 |
4,024 |
4,297 |
4,781 |
10 |
1,812 |
2,228 |
2,634 |
2,764 |
3,169 |
3,581 |
3,892 |
4,144 |
4,584 |
12 |
1,782 |
2,179 |
2,560 |
2,681 |
3,055 |
3,428 |
3,706 |
3,930 |
4,318 |
14 |
1,761 |
2,145 |
2,510 |
2,624 |
2,977 |
3,326 |
3,583 |
3,787 |
4,140 |
16 |
1,746 |
2,120 |
2,473 |
2,583 |
2,921 |
3,252 |
3,494 |
3,686 |
4,015 |
18 |
1,734 |
2,101 |
2,445 |
2,552 |
2,878 |
3,193 |
3,428 |
3,610 |
3,922 |
20 |
1,725 |
2,086 |
2,423 |
2,528 |
2,845 |
3,153 |
3,376 |
3,552 |
3,849 |
22 |
1,717 |
2,074 |
2,405 |
2,508 |
2,819 |
3,119 |
3,335 |
3,505 |
3,792 |
24 |
1,711 |
2,064 |
2,391 |
2,492 |
2,797 |
3,092 |
3,302 |
3,467 |
3,745 |
26 |
1,706 |
2,056 |
2,379 |
2,479 |
2,779 |
3,087 |
3,274 |
3,435 |
3,707 |
28 |
1,701 |
2,048 |
2,369 |
2,467 |
2,763 |
3,047 |
3,250 |
3,408 |
3,674 |
30 |
1,697 |
2,042 |
2,360 |
2,457 |
2,750 |
3,030 |
3,230 |
3,386 |
3,646 |
∞ |
1,645 |
1,960 |
2,241 |
2,326 |
2,576 |
2,807 |
2,968 |
3,090 |
3,291 |
|
|
|
|
|
|
|
|
|
|
244

Таблица 3 . 1 3
Некоторые значения квантилей нормального распределения
Р |
0,0250 |
0,0505 |
0,1003 |
0,1493 |
0,2006 |
0,2514 |
0,3015 |
0,3483 |
0,4013 |
0,4483 |
0,5000 |
0,5517 |
0,5987 |
0,6517 |
U p |
-1,96 |
-1.64 |
-1,28 |
-1,04 |
-0,84 |
-0,67 |
-0,52 |
-0,39 |
-0,25 |
-0,13 |
0,00 |
0,13 |
0,25 |
0,39 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
0,6985 |
0,7486 |
0,7996 |
0,8508 |
0,8997 |
0,9495 |
0,9750 |
0,9901 |
0,9990 |
0,0010 |
|
0,0099 |
|
|
U p |
0,52 |
0,67 |
0,84 |
1,04 |
1,28 |
1,64 |
1,96 |
2,33 |
3,09 |
-3,09 |
|
-2,33 |
|
|
246