
824
.pdf1.МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Вобщем виде постановка экстремальной задачи состоит в определении наибольшего или наименьшего значения целевой функции f(x1,x2,...,xn) при
условиях gi(x1,x2,...,xn)< = bi (i = 1...m), где f и gi – заданные функции, а bi –некоторые действительные числа.
Взависимости от свойств функций f и gi математическое программирование можно рассматривать как ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов решения определенных классов задач.
Среди задач математического программирования выделяют задачи линейного и нелинейного программирования. При этом если все функции f и
gi линейные, то соответствующая задача является задачей линейного программирования. Если же хотя бы одна из указанных функций нелинейна, то соответствующая задача является задачей нелинейного программирования.
Наиболее изученным разделом математического программирования является линейное. Для решения задач линейного программирования разработан целый ряд эффективных методов, алгоритмов и программ, причем
вданном разделе выделен класс специальных задач, которые рассматриваются ниже.
Среди задач нелинейного программирования наиболее глубоко изучены задачи выпуклого программирования. В результате решения этих задач определяется минимум выпуклой или максимум вогнутой функции, заданной на выпуклом замкнутом множестве.
Всвою очередь, среди задач выпуклого программирования более подробно исследованы задачи квадратичного программирования. В результате решения таких задач требуется в общем случае найти максимум (или минимум) квадратичной функции при условии, что ее переменные удовлетворяют некоторой системе линейных неравенств (или линейных уравнений), либо некоторой системе, содержащей как линейные неравенства, так и линейные уравнения.
Вкачестве особого класса задач математического программирования выделяют задачи целочисленного, параметрического и дробно-линейного программирования.
Взадачах целочисленного программирования неизвестные могут принимать только целочисленные значения.
Взадачах параметрического программирования целевая функция или функции, определяющие область возможных изменений переменных, либо и то и другое зависят от некоторых параметров.
Взадачах дробно-линейного программирования целевая функция представляет собой отношение двух линейных функций, а функции, опре-
11
деляющие область изменений возможных переменных, также являются линейными.
Выделяются отдельные классы задач стохастического и динамического программирования.
Если в целевой функции или функциях, определяющих область возможных изменений переменных, содержатся случайные величины, то такая задача относится к задаче стохастического программирования.
Задача, процесс нахождения решения которой является многоэтапным, относится к задаче динамического программирования.
12
2. ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Определение 1. Общей задачей линейного программирования (ЗЛП) называется задача, которая состоит в определении максимального (минимального) значения функции
n |
|
F cj xj |
(2.1) |
j 1 |
|
при условиях |
|
n |
|
aij xj bi , i = 1…k; |
(2.2) |
j 1 |
|
n |
|
aij xj bi , i = k + 1…m; |
(2.3) |
j 1 |
|
xj 0, j = 1…l, l n, |
(2.4) |
где aij, bi, cj – заданные постоянные величины и k m. |
|
Определение 2. Функция 2.1 называется целевой функцией (или линейной формой) задачи 2.1–2.4, а условия 2.2–2.4 – ограничениями данной задачи.
Определение 3. Стандартной (симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции 2.1 при выполнении условий 2.2 и 2.4, где k = m и l = n.
Определение 4. Основной (канонической) задачей ЛП называется задача, которая состоит в определении максимального значения функции 2.1.1 при выполнении условий 2.3 и 2.4, где k = 0 и l = n.
Определение 5. Совокупность чисел Х = (х1, х2, ..., хn), удовлетворяющих ограничениям задачи 2.2–2.4, называется допустимым решением (или планом).
Определение 6. План Х*, при котором целевая функция задачи 2.1 принимает свое максимальное (минимальное) значение, называется оптимальным.
Значение целевой функции при плане Х обозначим F(Х). Следовательно, если Х* – оптимальный план, то для любого Х выполняется F(Х) F(Х*).
Переход между формами ЗЛП:
–от минимума к максимуму;
–от ограничений неравенств к ограничениям равенствам;
–замена отрицательных переменных.
13
Если требуется найти минимум F, то можно перейти к поиску максимума – F.
Ограничение-неравенство вида можно преобразовать в ограничениеравенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение вида – в ограничение-равенство вычитанием из его левой части дополнительной переменной. Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений неравенств в ограничения равенства равно числу преобразуемых неравенств. Вводимые дополнительные переменные имеют определенный экономический смысл (объем неиспользуемого ресурса).
Если переменная хk не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными uk и vk, приняв
хk = uk – vk.
Векторная форма записи ЗЛП имеет вид: max F(Х* ) = CX
при ограничениях A1x1 + A2x2 + … + Anxn = B, x 0,
где C = (c1, c2,…, cn), Х = (х1, х2, ..., хn),
CX – скалярное произведение векторов C, X; Aj и B – вектор-столбцы.
Матричная форма записи ЗЛП:
max F(Х*) = CX,
при условиях AX = B, X 0;
здесь C = (c1, c2,…, cn) – вектор-строка; А = (aij) – матрица размерности m n, столбцами которой являются вектор-столбцы Aj.
2.1. Геометрическое решение задачи линейного программирования
Задача состоит в определении максимума целевой функции
n
F cj xj
j 1
при условиях
n
aij xj bi (i = 1...m);
j 1
xj 0 (j = 1...n).
14
Реально геометрическое решение имеется при наличии двух перемен-
ных х1 и х2.
Тогда задачу ЛП можно переписать в виде: найти максимум
F = c1x1 + c2x2,
при условиях
ai1x1 + ai2x2 bi (i = 1...k), xi 0.
Каждое из неравенств системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми:
ai1x1 + ai2x2 = bi (i = 1...k),
х1 = 0, х2 = 0.
В том случае, если система неравенств совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Множество точек пересечения данных полуплоскостей выпуклое (т.е. любые две точки, принадлежащие данному множеству, можно соединить отрезком, который также будет принадлежать данному множеству), и областью решений задачи ЛП является выпуклое множество, которое называется многоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.
Таким образом, исходная задача ЛП состоит в нахождении такой точки многоугольника решений, в которой целевая функция принимает максимальное значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим линию уровня
c1x1 + c2x2 = h,
где h – некоторая постоянная, проходящую через многоугольник решений, будем передвигать ее в направлении вектора С = (c1,c2) до тех пор, пока она не пройдет через последнюю ее общую точку с многоугольником решений. Координаты указанной точки и определяют оптимальный план данной задачи.
При геометрической интерпретации задачи ЛП могут встретиться следующие случаи (рис. 2.1.1):
целевая функция принимает максимальное значение в единственной точке (рис. 2.1.1, а);
15

максимальноезначениепринимаетсявлюбойточкеотрезка(рис. 2.1.1, б);
целевая функция не ограничена сверху на множестве допустимых решений (рис. 2.1.1, в.);
система ограничений несовместна (рис. 2.1.1, г).
Нахождение минимума целевой функции отличается тем, что линии уровня перемещаются не в направлении вектора С, а в противоположном направлении. Отмеченные выше случаи имеют место и при определении минимума целевой функции.
а |
б |
х2 |
х2 |
|
С |
|
|
|
С |
|
|
|
0 |
||
0 |
|
х1 |
|
х1 |
|
|
|
||||
|
|
|
|
||
|
в |
|
|
|
г |
|
|
|
|
|
|
х2 |
|
х2 |
|
||
|
С |
0 |
С |
|
0 |
х1 |
х1 |
||
|
||||
|
|
Рис. 2.1.1
16
Итак, нахождение задачи линейного программирования на основе ее геометрической интерпретации включает следующие этапы:
1)строят прямые, уравнения которых получаются в результате замены
вограничениях знаков неравенств на равенства;
2)находят полуплоскости, определяемые каждым из ограничений за-
дачи;
3)находят многоугольник решений;
4)строят вектор С;
5)строят прямую c1x1 + c2x2 = h, проходящую через многоугольник решений;
6)передвигают прямую c1x1 + c2x2 = h в направлении вектора С, в результате чего-либо находят точку (точки), в которых целевая функция принимает максимальное значение, либо устанавливают неограниченность сверху функции на множестве планов;
7)определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке.
Необходимо отметить, что поиск экстремума при решении задачи ЛП геометрическим методом можно осуществлять следующим образом: вычислив значения целевой функции в вершинах многоугольника решений, выбираем из них максимальное или минимальное. При этом необходимо определить координаты вершин многоугольника решений путем составления и решения систем линейных уравнений (вершина лежит на пересечении прямых, уравнения которых получены путем преобразования неравенств системы ограничений в равенства). Координаты вершин, в которых достигается экстремум, определяют оптимальный план задачи.
Пример 2.1.1
Для производства 2-х видов конструктивных плит (А и Б) на заводе железобетонных конструкций используется 3 вида сырья. Нормы расхода сырья каждого вида на изготовление одной плиты соответствующего вида приведены в табл. 2.1.1. В ней же указаны прибыль от реализации изделия каждого вида и общее количество сырья каждого вида, которое может быть использовано предприятием.
|
|
|
|
Таблица 2 . 1 . 1 |
|
|
Нормы расхода сырья |
Общее количество |
|
|
|
сырья |
||
|
|
|
|
|
Вид сырья |
А |
|
Б |
|
1 |
12 |
|
4 |
300 |
2 |
4 |
|
4 |
120 |
3 |
3 |
|
12 |
252 |
Прибыль |
30 |
|
40 |
|
|
|
17 |
|
|
Учитывая, что изделия А и Б могут производиться в любых соотношениях (сбыт обеспечен), требуется найти такой план производства, при котором прибыль предприятия будет максимальной.
Предположим, что предприятие изготовит x1 изделий вида А и x2 изделий вида Б. Так как производство продукции ограничено имеющимися в распоряжении предприятия сырьевыми ресурсами и количество изделий не может быть отрицательным, должны выполняться следующие неравенства:
12x1 + 4x2 ≤ 300;
4x1 + 4x2 ≤ 120;
3x1 + 12x2 ≤ 252;
x1 0;
x2 0.
Общая прибыль от реализации x1 изделий вида А и x2 изделий вида Б составит:
F(X) = 30x1 + 40x2.
Таким образом, требуется среди всех неотрицательных решений данной системы линейных неравенств найти такое, при котором функция F принимает максимальное значение.
Определение многоугольника решений. В неравенствах системы огра-
ничений и условиях не отрицательности переменных заменяем знаки неравенств на знаки равенств и строим соответствующие прямые (рис. 2.1.2):
12x1 + 4x2 |
= 300; |
(I) |
||
4x1 |
+ 4x2 = 120; |
(II) |
||
3x1 |
+ 12x2 |
= 252; |
(III) |
|
|
x1 |
= 0; |
(IV) |
|
|
x2 |
= 0. |
(V) |
|
18

Рис. 2.1.2
Прямые (IV) и (V) представляют собой оси координат. Каждая из построенных прямых делит плоскость на две полуплоскости, в одной из которых выполняется соответствующее неравенство, а в другой нет. Для определения полуплоскости, в которой неравенство выполняется, берем любую точку (например, (0,0)) и подставляем ее в исходное неравенство. Если неравенство выполняется, то искомая полуплоскость включает точку (0,0), иначе – рассматриваем другую полуплоскость. Пересечение полученных полуплоскостей определяет многоугольник решений (на рис. 2.1.2 он выделен жирной линией). Координаты любой точки, принадлежащей данному многоугольнику, удовлетворяют системе ограничений и условиям неотрицательности переменных. Следовательно, необходимо найти такую его точку, в которой целевая функция принимает максимальное значение.
Поиск максимума целевой функции. Строим вектор С (30, 40) и прямую
30x1 + 40x2 = 480 (число 480 выбрано произвольно). Если взять любую точку, принадлежащую данной прямой и многоугольнику решений, то ее координаты определяют такой план производства, при котором прибыль рав-
на 480.
Перемещаем построенную прямую в направлении вектора С до тех пор, пока не достигнем единственно точки пересечения с многоугольником решений (на рис. 2.1.3 это точка А). Координаты этой точки определяют оптимальный план задачи.
19
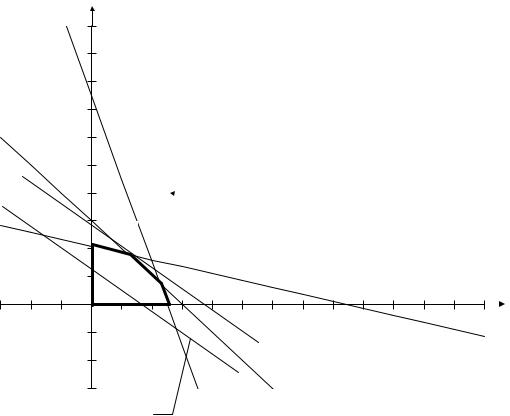
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-30 |
-20 |
-10 |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
|
|
-10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-20 |
|
|
|
|
|
|
x1 |
|
|
|
|
|
(III) |
|
|
|
-30 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
(I) |
|
|
(II) |
|
|
|
|
|
|
|
|
|
30x1+40x2 =480 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 2.1.3
Координаты точки А определяются из следующей системы (точка А лежит на пересечении прямых (II) и (III)):
4x1 + 4x2 = 120;
3x1 + 12x2 = 252.
Решив данную систему, получим
x1* = 12, x2* = 18.
Максимальное значение целевой функции при оптимальном плане
X* = (12, 18) равно
Fmax = 30 12 + 40 18 = 1080.
Следовательно, если завод железобетонных конструкций изготовит 12 плит вида А и 18 плит вида Б, то его прибыль будет максимальной и равной 1080.
Отметим, что найти максимальное значение целевой функции можно было и путем вычисления ее значения во всех вершинах многоугольника решений.
Задания для решения задач ЛП геометрическим методом приведены в конце учебного пособия.
20
