Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

802

.pdf

Скачиваний:

Добавлен:

16.06.2024

Размер:

754.59 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

С математической точки зрения кинетические процессы во многих дисперсных системах могут быть описаны дифференциальным уравне

нием второго порядка (W p T1 p 1 k T2 p 1 ). При анализе таких кинетических процессов необходимо учитывать не только скорость изменения контролируемого параметра, но как минимум и ускорение.

В отклонениях от равновесного состояния x = xm здесь будем иметь:

z 2n z 02 z 0

n 0 .

Пусть k1,2 1,2

– корни характеристического уравнения

k2 2nk 2 0 .

Рассмотрим сначала случай

n2 2 0 .

Имеем

z c e

1t c e 2t

где

n n2 2 ;

n n2 2

;

При z 0 xm ,

z 0 0 с учетом

z t c1 1e 1t c2 2e 2t

будем иметь

z 0 c1 c2 xm ,

z 0 c1 1 c2 2 0 .

Откуда

xm ,

xm .

Тогда

e 1t

e 2t ,

2 e

1 t

1 e

2 t

xm .

(3)

(4)

Имеем

z x c1 12 e 1 t c2 22 e 2 t .

Из x = 0 следует
	2					t	2								t	0 .
	2 1		x	m	e	1	1 2				x	m	e	2
		2	x		e	1				2	x		e	2

1							1
Откуда
			e 1 tn					2	e 2 tn ,
				1				2

или

1 e 1 2 tn .

Так что точке перегиба соответствует значение t = tn, определяемое из условия

	t	n		1		ln	1				(5)
	t					ln					(5)
					2			2
				1	2			2
(при t = tn вогнутость сменяется на выпуклость).
Займемся определением 1			и 2 по x(t), полученной эксперимен9
тально. Так как	< , то в (4)			составляющая						xm		e 1 t затухает
тально. Так как	< , то в (4)			составляющая					2			e 1 t затухает
2	1								2		2
									1		2

быстрее, чем аналогичная составляющая, соответствующая корню 2. Поэтому значение 2 можно определить по концу экспериментально полученного процесса x(t).

Без ограничения общности рассуждений можно принять xm = 1 (равносильно масштабированию x(t)).

В силу предыдущего

1	x t		1	2 e 1 t 1 e 2 t .					(6)
1	x t	1		2 e 1 t 1 e 2 t .					(6)
		1	2
Определим значение t1 такое, чтобы при t > t1 выполнялось
	1 x t							2 t
	1 x t				1			e .
					1 2
Должны иметь
		e 2 t				2	e 1 t
		1				2

или

e 1 2 t ,

или

1 2 t .

Откуда

или

tn t,

t tn .

Таким образом,

1 x t

2 t

1 2

при t>>tn.

Введем

y t 1 x t Ae 2 t .

Тогда

y t T Ae 2 t T .

Откуда

y t

Ae 2 t

e 2

y t T

Ae 2 t T

или

2 T ln ,

или

2 T .

Далее из x 0 следует

1 e 1 tn 2 e 2 t ,

	r e r 2 t e 2 t ,																												1
																					r								1			1		,
																					r											1		,
																													2
r e r 1 2 t , ln r r 1 2 t,																					1													1
																					1					ln r 2 t, ln r										r 1	2 t.
																										ln r 2 t, ln r										r 1	2 t.
																				r 1
Откуда
														1								2 tn
												r r 1 e																.						(7)
Рассмотрим функцию
																			1
											y r						r 1				.
Имеем
							ln y									1					ln r ,
							ln y								r	1					ln r ,
															r	1
				1																								1				ln r
	y					r	1			ln r												1
																												r
			r
			r																																,
	y											2																					2		,
							r 1					2															r 1						2
							r 1																				r 1

																			1
									1				1									ln r
									1				1						r			ln r

					y r r 1																										.
					y r r 1																				2						.
																		r 1							2
Отсюда y 0 при r 1.
Справедливо
							1																		1
							1	lim																				e,

		lim r r 1

																1
		r 1									0
										r 1.
																								1
Так что в интервале (1, )																y r							r 1							не превышает e. Поэтому
уравнение (6) имеет решение r 1 лишь при e 2 tn																																		e .
Откуда следует
						2 tn 1,																												(8)
и 2 должно удовлетворять условию
							t						1			.																		(9)
							t	n								.																		(9)
								n							2
															2

При этом 2max n (тогда 1				2,						n 0 ).
Из (5) следует
			t				1					ln		1
		2	t	n			1		1			ln		2
		2		n			1
							2
							2
или
								ln r			.	(10)
											.	(10)
								r 1
Из
					1
	d			1				ln r					< 0
	d			1		r		ln r

	d r				r		1			2
	d r				r		1

следует, что 2 tn с ростом r уменьшается. Отметим,

d y	r	1	d	.
		r 1
d r
			d r

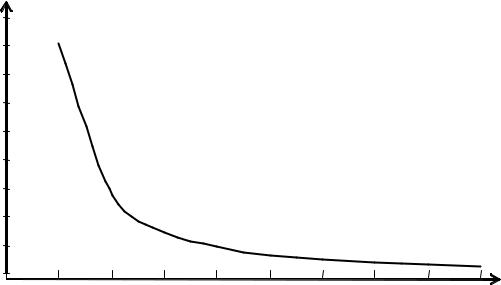
График функции r r , полученный аппроксимацией табличных значений решений уравнения (8) при различных 2 tn методом наименьших квадратов, приводится на рис. 3.9.

r
45
40		r(v) 11376,v 1.5518
35		r(v) 11376,v 1.5518
35
30
25
20
15
10
5
0									0,9 v
0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9 v

Рис. 3.9. Вид функции r = r( )

Определим зависимость корней 1, 2 (определяют вид кинети9 ческого процесса) от параметров модели 0 и n (определяют упругие и демпфирующие свойства материала).

Из

1 n n2 02

2n,

2 n n2 02

n2 02

следует

2 n 1 2n .

При этом 1 2				при		n 0 .
Справедливо
1 1			n		0,
1 1					0,
n		n2 02
	1			0			0,
	0						0,
	0			n2 2
					0
2				2			0,
1				0
1
n2		n2 02 3
2				2		0,
1				0
1
02		n2 02 3

2	1	n	0,

n		n2 02

	2			0	0,
	0			n2 2	0,
	0			n2 2
				0
2				2		0,
			2	0
			2
n2				n2 02 3
2		2		2		0.
				0

2				n2 02 3

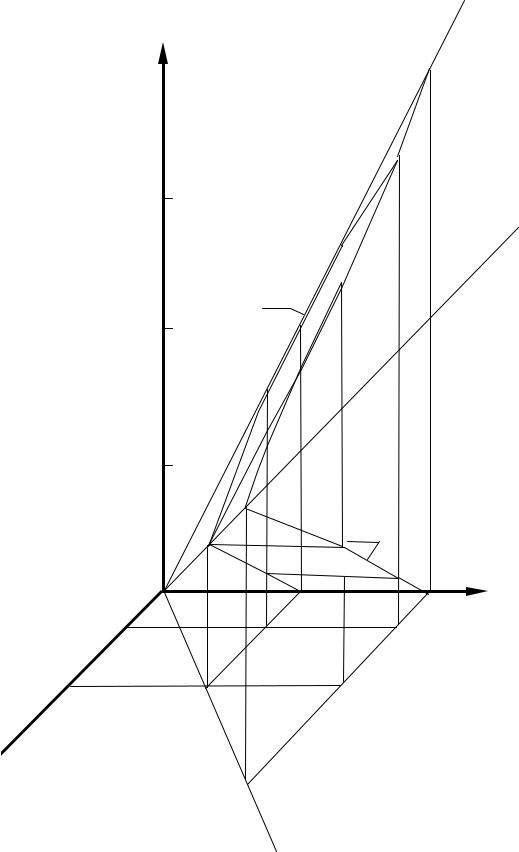
Вид зависимостей 1 1 0,n и 2 2 0 ,n приводится на рис. 3.10.

Введем безразмерный коэффициент демпфирования n , n 0 ,

1. Его величина определяется структурой и физико9химическими свойствами материала.

	Имеем			1								1 0 ,								1 0
				1						2		1 0 ,				2		2		1 0		;		(11)
														2	2		2 1;
											1			2		0
		2 1						2 1							2 1				2	1	2	1	2
	r																						1	;
	r	2 1			2 1 2 1																	02	1	;
		r ;					r;					1	.
		r ;				2	r;		2				.
1	0		1			2			2			r	0
												r

	1 0,n 2n

3 0

	1	P
~
2 0
	M	1 0 , 0 n 0

	2
~		2 0,n 0
~
0		~	n
		2 0	n

Рабочая

зона

n 0

Рис. 3.10. Вид функций 1 1 0 ,n и 2 2 0 ,n

Справедливо

				r				2 1																									2							2 1
																			2																						2
						2						1													2											1										=
																	1																								1
																			2				1 2									2
													2																							r.
													2			2 1														2 1						r.
																2 1														2 1
		Откуда следует
														r				0									1.

		Как видим, с ростом значение																								1	растет.
		Как видим, с ростом значение																								2	растет.
																										2
		Из
	2r						r	2 1 r											1											2							2 1										1
				2																						2									r					r									=
			2	2							2		1					2								2									r					r		2					2	1	=
													1							1										2	1												1					1
																															1
																											2r							2 2 1 ;
								2r 2
								2r 2		2					2																		3
												1							1									2
												1							1									2	1
																													1
																					d 2r					0;
																				d 2						0;
																				d 2
получим
									2 2 1;															3 2 4;													2	.
									2 2 1;															3 2 4;												3		.
																																				3
		Так,				что		функция					r r									имеет							перегиб в										точке				с	абсциссой
		2			, при этом при						1							2					функция выпукла, при																						2			– во9
					, при этом при						1								3				функция выпукла, при																									– во9
			3																3																									3
гнута.
		Легко заметить, что функция r r																														является решением диффе9
ренциального уравнения
														d r								2					r 0.
														d									2			1	r 0.
														d									2			1

Имеем

			d r		2		d			,	1.
					2					,	1.
			r				2 1
Откуда
ln	r	2	d			,	ln	r	2ln			2		1	ln c,


			2
			2
				1
				r c 2 1 2 .
При начальном условии r 0 0											02 1		2	получим: с = 1.
Откуда

r 2 1 2 .

Далее рассмотрим связь между характеристиками кинетических процессов и параметрами модели.

Изменение структуры и физико9химических свойств материала приводит к изменению расположения точки перегиба. Определим связь между абсциссой точки перегиба и параметрами 0, n модели

(или	n	и ).
(или		и ).
	0	0
	0
Из формул (5), (11) следует
					1		n	n2 2
		t	n			ln		0	.
		t				ln			.
				2	n2 2		n	n2 2
				2	n2 2		n	n2 2
					0			0

Откуда

										n	n	2	2					2
tn		1						ln		n	n				n		n
tn		1											0	2	n		n		1	=
														2					1	=
0	n2	02		n	2					n n2 02					0		0
2				n		1
2				0		1
				0
					1						ln r 2 2 1					.

			2 n2 02				n		2
										1

							0
							0

В силу n2 2			отсюда следует,												что знак				tn	определяется знаком
В силу n2 2			отсюда следует,												что знак					определяется знаком
	0																		0
																			0
функции	y ln r 2					2 1 .		Так							как			y 0 1, то					значение tn
убывает с ростом ( > 0,											n			1 ).
убывает с ростом ( > 0,														1 ).
			0		0						0
											0
Также справедливо
					n					2 n					2		2		n n		2	2
		tn			n					2 n						0			n n			0
		n	n		2	2	3								n			ln n n2 02
	2		n			0
		n							1													n 0 .
		n				2 1			1				ln r				0		1
				3		2 1							ln r				0		1
		2 n2 02		3								2
		2 n2 02

Откуда следует, с ростом n значение tп уменьшается, точка перегиба смещается влево.

Таким образом, для увеличения значения tп следует уменьшить 0 и n (предполагается выполнение условия n 0 ).

При разработке материалов следует учитывать зависимости 2 и r от ,

0, n. Имеем

r r , n0 0 ,n .

Справедливо

r	d r	d r	n
				.
0	d 0		0
		d
			2

Отсюда с учетом	d r	0	1 следует	r	0	1.
Отсюда с учетом	d	0	1 следует		0	1.
	d
				0

Также справедливо

Имеем

d r

d n

d r

0 d

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.06.2024751.5 Кб0799.pdf
#
16.06.2024115.05 Кб08.pdf
#
16.06.2024180.31 Кб080.pdf
#
16.06.2024751.69 Кб0800.pdf
#
16.06.2024753.83 Кб0801.pdf
#
16.06.2024754.59 Кб2802.pdf
#
16.06.2024762.42 Кб0803.pdf
#
16.06.2024762.73 Кб0804.pdf
#
16.06.2024763.4 Кб0805.pdf
#
16.06.2024764.37 Кб0806.pdf
#
16.06.2024765.04 Кб0807.pdf