Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

744

.pdf

Скачиваний:

Добавлен:

16.06.2024

Размер:

679.39 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

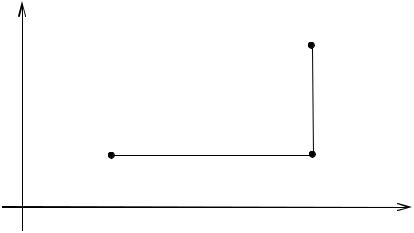
Выполняется равенство

P Q 8xy.y x

Следовательно, данное выражение действительно является полным дифференциалом некоторой функции.

Справедливо:

u x, y L	x, y		x, y
					x2 y2
	x0 , y0	Pdx Qdy C L		4x	x2 y2	dx
	x0 , y0		x0 , y0
		4 y x2 y2 dy C,

где криволинейный интеграл в правой части равенства можно брать по любому пути L.

Выберем в качестве пути интегрирования L ломаную, состоящую из двух звеньев L1, L2 параллельных осям координат .

		(x,y)
		L2
		(x1,y0)
(x0,y0)	L1	x

Тогда

x, y

u x, y L

x2 y dx 4 y

x2 y2

x0 , y0

x, y

y2 dx 4 y

dy.

x0 , y0

Но на L1 y y0 const,

dy 0;

на L2

x const, dx 0.

Следовательно,

u x, y

x2 y02 xdx 4 x2 y2 ydy c.

Обыкновенные дифференциальные уравнения

Задание 1. Решить уравнение y2 1dx xy dy .

Решение. Разделив левую и правые части уравнения на выражение

x y2 1	(при x 0), приходим к равенству			dx	ydy	. Интегрируя, по-
x y2 1	(при x 0), приходим к равенству			x		. Интегрируя, по-
				x	y2 1
лучим:
		dx	ydy
		x	y 1

или

ln x y2 1 C .

Задание 2. Решить уравнение y x2 y2 0 . xy

Решение. Заменив x на kx, а y на ky, заметим, что уравнение не изменилось. Это доказывает, что оно однородное.

Введя y=ux ( y u x u ), получим:

u x u x2 u2 x2 0 xux

или, сокращая на x2:

u x u 1 u2 0, u

u x 1 u2u2 0 , dudx x 1 u2u2 .

Получили уравнение с разделяющимися переменными, которое после разделения переменных запишется следующим образом:

1 u2u2 du dxx .

Интегрируя, имеем:

14 ln 1 2u2 ln x ln C

или

Заменив u на

	1
или C :

	C

	1	Cx4 .
	1 2u2	Cx4 .
	1 2u2

xy , получим:

		1			Cx4 ;
1			2 y2		Cx4 ;
			2 y2
			x	2
			x	2
		x2			Cx	4	,
x2	2 y2				Cx		,
x2	2 y2
		1			Cx2		,
x2	2 y2				Cx2		,
x2	2 y2

x2 x2 2 y2 C1

x2 x2 2 y2 C .

Задание 3. Проинтегрировать уравнение y

2xy

arctgx .

1 x2

Решение. Это уравнение Бернулли. Сделав замену

y uv, y

u v uv

получим:

2xv

u v

arctg x .

1 x

1 x2

Примем за v какое-либо частное решение уравнения

			2xv
		v		0 .
		v	1 x2	0 .
Разделяя в нем переменные, находим:
dv	2xdx	; ln v ln 1 x2 ; v 1 x2
v	1 x2	; ln v ln 1 x2 ; v 1 x2

(постоянную интегрирования не вводим).

Для отыскания u имеем уравнение

	uv
	1 x2
u x 4	1 x2	arctg x ,

или (поскольку v 1 x2 )

		u			4 u arctgx				dx ,
		u			1 x2				dx ,
				u arctg2 x C .
Таким образом, u arctg2 x C 2						и y uv arctg2 x C 2 1 x2 .
Задание 4. Решить уравнение 3x2 6xy2 dx 6x2 y 4 y2 dy 0 .
Решение.	P x, y 3x2 6xy2 Q x, y 6x2 y 4 y2
		P	12xy				Q	12xy ,
			12xy				x	12xy ,
		y					x
значит, данное уравнение в полных дифференциалах, то есть
	U x, y				U dx			Q dy 0 ,
					x			y
U	3x2 6xy2				и				U 6x2 y 4 y2 .
x									y

Интегрируя Ux по x, получим:

U x, y 3x2 6xy2 dx x3 3x2 y2 y .

Продифференцируем полученное выражение по y:

y y ,

но

y 4 y

, тогда 6x

y 4 y

4 y

. Откуда

4 y3

C , а U x, y x3

3x2

4 y3

C 0 – общий интеграл данно-

го уравнения.

Задание 5. Проинтегрировать уравнение ydx x2 y x dy 0 .

Решение.

	P x, y y ,	Q x, y x2 y x ,
P	1,		Q	1 2xy ,
y			x
	P	Q	,
	y	x

то есть уравнение не является уравнением в полных дифференциалах. Найдем интегрирующий множитель. (Интегрирующим множителем для

уравнения P x, y dx Q x, y dy 0 называется такая функцияx, y 0 , после умножения на которую уравнение превращается в уравнение в полных дифференциалах. Если функции P x, y и Q x, y в уравне-

нии имеют непрерывные частные производные и не обращаются в нуль одновременно, то интегрирующий множитель существует) Рассмотрим разность

2 1 xy ,

Q x, y x2 y x x 1 xy .

зависит только от x. Тогда

Выражение

Q x, y

e 2ln

1 .

Умножая обе части уравнения на

x 0

, получим уравнение

dx y

dy 0 ,

которое является уравнением в полных дифференциалах.

U	y		U		1
				y
x	x	2	y		x

U x, y 1x y y ,

U	1		y или	U	1	y .
y	x		y или	y	x	y .

Откуда

y y ,

y y2 C , 2

U x, y y2 y C , 2 x

y2 y C – общий интеграл. 2 x

Задание 6. Найти общее решение уравнения y 1x . Решение. Последовательно интегрируя, получим:

1 dx = ln

C1 ,

du dx

u ln

C dx

dx C

v dx x

dv dx

x ln x x dxx C1 dx x ln x x C1x C2.

y x ln x x C1x C2 dx x ln x dx C1 xdx C2 dx

u ln

du dx

dv xdx

v xdx

x2dx

xdx C

C .

x x 1 при

Задание 7. Найти частное решение уравнения

x 1

y 2 1, y 2 1.

Решение. Введем y p p

x x 1 ,

x 1

или

p x x 1 .

x 1

Это линейное уравнение.

Введем

p uv dp

v du

u dv

v du

u dv

uv x x 1 ,

x 1

Откуда v x 1.

Исходное уравнение будет иметь вид:

x 1 dudx x x 1 , x 1.

Откуда

x ,

C .

Тогда

y p

C1x C1 .

Интегрируя, получим:

1 x

C x

Из начальных условий

y 2 1, y 2 1

следует

C1 3, C2 13.

Откуда

y 241 3x4 4x3 36x2 72x 8 .

Задание 8. Решить уравнение y 2 y y 3 0 .

Решение. Замена

p y

, y

p dy

приводит к уравнению первого

порядка:

p dp

2 yp3

или

2 ydy .

Интегрируя, получим:

y2 C

то есть

y2 C

или

y2 C1 dy dx .

Витоге получим общий интеграл исходного уравнения:

				y3	C y x C	2	.
					C y x C		.
			3		1
			3
Задание 9. Найти общее решение уравнения: y 7 y 6 y 0 .
Решение.	Составим характеристическое уравнение k2 7k 6 y 0 ;
его корни k 6, k		2	1. Следовательно, e6 x			и ex – частные линейно неза-
1		2

висимые решения, а общее решение имеет вид y C1e6 x C2ex .

Задание10. Найти общее решение уравнения y 4 y 13y 0 . Решение. Характеристическое уравнение имеет корни k1,2 2 3i .

Корни характеристического уравнения комплексные сопряженные, поэто-

му им соответствуют частные решения

e2x cos3x

и e2 x sin 3x . Следо-

вательно, общее решение имеет вид

y e2 x C cos3x C

sin3x .

Задание 11. Найти частное решение уравнения

y 2 y y 0 при

y 0 1, y 0 0 .

Решение. Решая характеристическое уравнение

k2 2k 1 0 , полу-

чим k k

1. Общее решение имеет вид

y C C

x ex .

Найдем такие

значения постоянных C1 и C2 , при которых выполняются заданные на-

чальные условия. Так как y 0 1,

то C1 1 и, поскольку

y y C2ex и

y 0 0 ,

то C2 1. Таким образом, окончательно получим частное ре-

шение

y 1 x ex .

0 x .

Задание12. Решить уравнение y

y sin x

Решение. Характеристическое

уравнение

k2 1 0

имеет корни

k1,2 i . Общее решение однородного уравнения имеет вид

y0 C1 cos x C2 sin x .

Будем искать частное решение неоднородного уравнения в виде y C1 x cos x C2 x sin x .

Решая систему
	C1 x cos x C2 x sin x 0
	C1 x sin x C2 cos x				1	,
	C1 x sin x C2 cos x				sin x	,
					sin x
получим:
C1 x	dC1 x	1,	C2 x	dC2 x
C1 x	dx	1,	C2 x
	dx				dx

cos x . sin x

Интегрируя, найдем:
C	x x C ,	C	2	x	cos x dx ln	sin x	C	2	.
C	x x C ,	C		x	cos x dx ln	sin x	C		.
1	1				sin x
					sin x

Общее решение будет иметь вид:

y x C1 cos x ln sin x C2 sin x .

Задание 13. Найти общее решение уравнения: y 2 y 10 y xcos 2x . Решение. Соответствующее однородное уравнение

y 2 y 10 y 0 .

Его характеристическое уравнение

k2 2k 10 0

имеет корни:

k1,2 1 3i .

Общее решение однородного уравнения имеет вид: y0 ex C1 cos3x C2 sin3x .

Частное решение неоднородного уравнения будем искать в виде: y Ax B cos2x Cx D sin 2x .

Имеем:

y Acos 2x 2 Ax B sin 2x C sin 2x 2 Cx D cos2x y 4Asin 2x 4 Ax B cos 2x 4C cos 2x 4 Cx D sin 2x

4Asin 2x 4 Ax B cos 2x 4C cos 2x 4 Cx D sin 2x2Acos 2x 4 Ax B sin 2x 2C sin 2x 4 Cx D cos 2x

10 Ax B cos2x 10 Cx D sin 2x xcos 2x .

Подставляя в исходное уравнение, получим тождество: xcos 2x

6Ax 4Cx 2A 6B 4C 4D cos2x

4Ax 6Cx 4A 4B 2C 6D sin 2x

Сравнивая коэффициенты при cos2x и sin 2x в левой и правой частях этого равенства, получим:

x 6A 4C x 2A 6D 4C 4D, 0 4A 6C x 4A 4B 2C 6D.

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.06.2024177.48 Кб074.pdf
#
16.06.2024674.16 Кб0740.pdf
#
16.06.2024674.3 Кб0741.pdf
#
16.06.2024674.54 Кб0742.pdf
#
16.06.2024676.7 Кб0743.pdf
#
16.06.2024679.39 Кб3744.pdf
#
16.06.2024680.06 Кб0745.pdf
#
16.06.2024680.5 Кб0746.pdf
#
16.06.2024681.69 Кб0747.pdf
#
16.06.2024685.43 Кб0748.pdf
#
16.06.2024686.32 Кб0749.pdf