Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

744

.pdf

Скачиваний:

Добавлен:

16.06.2024

Размер:

679.39 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 106 7 8 9 10 > Следующая >>>


Задание 2.	Для комплексного числа z 5 2i записать z .
Решение. Если комплексное число имеет вид z x iy , то сопряжен-
ное ему комплексное число			имеет вид:			x iy . Значит		5 2i .
ное ему комплексное число		z	имеет вид:		z	x iy . Значит	z	5 2i .
Задание 3.	Найти значение функции			f z 3z2 в точке z0 2 3i .

Решение. Подставим в функцию f z 3z2 вместо переменной z число z0 2 3i . Тогда

f z0 3 2 3i 2 3 4 12i 9i2 3 4 12i 9 3 5 12i 15 36i .

Задание 4. Найти значение производной функции f (z) 2 z3 в точке z0 i .

Решение. Найдем производную от данной функции: f z 3z2 ; значение производной в точке z0 i

f i 3i2 3.

Задание 5. Найти неопределенные интегралы.

a)	x 9				dx.
a)	4x	2			dx.
	4x		13
Решение. Разбив данный интеграл на два, получим интегралы, сводя-
щиеся к табличным интегралам вида:
						du				ln			u		c		и					du						1 arctg u					c,
																						du
																						2			2
							u														u		a					a				a
										x 9						dx			xdx						9						dx
									4x		2	13				dx		4x		2			13		9				4x		2	13
									4x			13						4x					13						4x			13
				1			8xdx							9							dx									1	ln 4x		2	13
				8			4x	2			Б13			9			2x 2							13		2				8	ln 4x			13
				8			4x				Б13						2x 2							13						8
																9	1		arctg					2x			c.
																9	13		arctg					1Б3			c.
																2	13							1Б3

б) 2x 3 cos 32x dx.

Решение. Используем формулу интегрирования по частям:

u dv uv v du.

2x 3 cos 3x

u 2x 3

du 2dx

dv cos 2

v 3 sin

3 sin

4 sin

dx 2 2x 3 sin 3x

8 cos

в)

3x3 x2 5x 1

Решение. Поделив числитель на знаменатель, представим неправильную дробь в виде суммы целой и дробной частей:

3x3 xx32 x5x 1 3 x2 x3 2xx 1.

Разложим правильную дробь на простейшие:

x2 2x 1			A	Bx C
	2		x	x	2	1
x x		1

Ax2 A Bx2 Cx .

xx2 1

Приравнявчислители, найдемA,B,C изусловияравенствамногочленов:

A B x2 Cx A x2 2x 1.

A B 1

Решив систему, имеем A = 1, B = 0, C = 2.

Тогда

dx 3x ln x 2arctgx C.

г)

3sin x cos x 2

Решение. Применив универсальную тригонометрическую подстановку

t и заменив sin x

cos x

1 t2

2dt

получим:

1 t2

2dt

t2 2

6t 3

1 t2

1 t

	2		dt				2			d t 3
	2		t 3	2	6		2	t 3 2					6	2
			t 3		6			t 3 2					6
	1		t 3 6						1		tg	x	3 6
												x

2		ln				c				ln		2			C.
2	2 6	ln	t 3 6			c			6	ln		x		6 3	C.
											tg
											tg	2

Задание 6. Вычислить определенный интеграл

9	x dx
		.

4	x 1

Решение. Сделав замену x t2 и найдя новые пределы интегрирова-

ния, получим: dx 2tdt, t2 4, t 2, t2 9, t 3

9	x dx	3						3	t	2	1 1
	x dx		t 2tdt			2			t		1 1
			t 2tdt			2
4	x 1	2		t 1				2			t 1
3		1				t2							3


2 t 1				dt	2			t ln				t 1
2 t 1		t 1		dt	2		2	t ln				t 1
2		t 1					2						2

2	9	3 ln 2 2 2		9 2 2ln 2 7 2ln 2.
2	2	3 ln 2 2 2	ln1	9 2 2ln 2 7 2ln 2.
	2

Задание 7. Вычислить интеграл ex2 dx по формуле Симпсона, разбив

интервал интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Решение. Для вычисления данного интеграла по формуле Симпсона

	b	f x dx b a y0 y2n 2 y2 y4 ... y2n 2
		f x dx b a y0 y2n 2 y2 y4 ... y2n 2
	a		6n
	a		4 y1	y3 ... y2n 1 ,
			4 y1	y3 ... y2n 1 ,
где a 0,	b 1,	2n 10,	n 5,	y ex2 ,введем обозначения:

y0 y2n 1, y2 y4 ... y2n 2 2 , y1 y3 ... y2n 1 3 .

Составим таблицу значений подынтегральной функции, записывая ординаты с четными и нечетными номерами в разные столбцы. В последней строке запишем результаты суммирования по этим столбцам.

i	xi		yi exi2
		при i=0, i=10	при четном i	при нечетном i
0	0	1
1	0,1			1,010
2	0,2		1,041
3	0,3			1,094
4	0,4		1,174
5	0,5			1,284
6	0,6		1,433
7	0,7			1,632
8	0,8		1,896
9	0,9			2,248
10	1	2,718
		1=3,718	2=5,544	3=7,268

ПодставивполученныерезультатывформулуСимпсона, получим:

1	1	3,718 2 5,544 4 7,268 1,463.
ex2 dx
	30
0

Задание 8. Вычислить несобственные интегралы или установить их расходимость.

0			dx
а)			dx				.
а)	9x	2	6x 2				.
	9x		6x 2
Решение.
			0			dx						0		dx					1		0		d		3x 1
						dx				lim				dx					1	lim
				9x	2	6x 2				lim			3x	1		2				lim		3x 1				2
				9x	3	6x 2					a a		3x	1			1		3 a a			3x 1					1
					3						3x	a		3 a				arctg1-arctg
				1 lim arctg							3x	1	0	1 lim				arctg1-arctg						3a+1
								1						1						1	3				.
								3				2			4					3	4			4	.
								3	4			2		3	4			2		3	4			4

Предел существует, значит, несобственный интеграл сходится.

5	dx
б)
	x 2	3
2

Решение. Подынтегральная функция													f x					1		имеет разрыв при
Решение. Подынтегральная функция													f x		x				2 3	имеет разрыв при
															x				2 3
x = 2, поэтому		5											5
		5			dx								5	dx
					dx				lim					dx
				x	2			3	lim					2		3
		2		x	2					0		2 x		2
lim		1					5				1			1		1			.
													lim
	2	x	2			2					2		lim	9			2
0	2	x	2				2				2		0	9
0													0

Предел бесконечен, несобственный интеграл расходится.

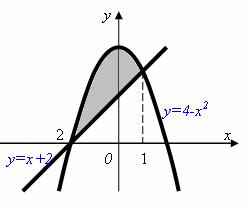
Задание 9. Найти площадь фигуры, ограниченной линиями y 4 x2 , y x 2 .

Решение. Изобразим графики указанных кривых на координатной плоскости:

Фигура, площадь которой необходимо найти, заключена между кривыми y 4 x2 , y x 2 . Абсциссы точек пересечения этих кривых равны

-2 и 1.

Площадь криволинейной трапеции найдем с помощью интеграла

S f1 x f2 x dx . Получим, что площадь данной области равна:

1	4 x2						1							1	2 x2 x dx
S	4 x2		x 2 dx					4 x2 x 2 dx							2 x2 x dx
2							2							2
		2x		x3	x2	1	2		1	1	4	8	2	4,5 кв.ед.
				x3	x2	1			1	1		8
						2
			3		2	2			3	2		3

Задание 10. Вычислить объем тела, образованного вращением вокруг

оси OX фигуры, ограниченной линиями: y 2									1		x	2		, x = –2, x = 1, y = 0.
оси OX фигуры, ограниченной линиями: y 2									1		9			, x = –2, x = 1, y = 0.
											9
Построим фигуру, ограниченную указанными линиями.
Преобразуем первое из этих уравнений:
y	2		x2		y2		x2			x2			y2
		4 1		,		1		,							1.
		4 1		,		1		,							1.
			9		4		9		9				4

-2

Первое уравнение определяет верхнюю половину эллипса с полуосями a = 3, b = 2.

Воспользуемся формулой

Vx y2dx.

							a
1		x2						x3			1		1		8
1		x2						x3			1		1		8
Vx	4 1		dx 4			x						4 1		2
Vx	4 1		dx 4			x		27				4 1	27	2	27
2		9						27			2		27		27
2		9									2
						9			32
			4 3									куб.ед.
			4 3		27					3		куб.ед.
					27					3
Задание 11. Вычислить двойной интеграл x3 y3 dxdy ,																если об-
				1 x,								D
ласть D ограничена линиями y				1 x,			y x,					x 4.
				2

Решение. Построим заданную область D.

y
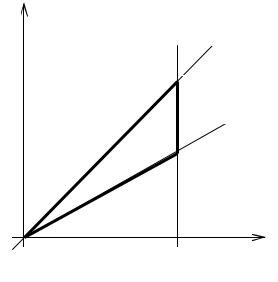
y	y x

y 12 x

x = 4

0	4
0	4	x

Контур этой области пересекается всякой прямой, параллельно оси Oy в двух точках. Внутреннее интегрирование производится по переменной y, а внешнее – по x:

x3	4	x	x3 y3 dy .
x3	y3 dxdy dx		x3 y3 dy .
D	0	1
		2 x
			x	x3 y3 dy ,
Вычисления следует начинать с внутреннего интеграла				x3 y3 dy ,
			1 x
			2

в котором величина x должна рассматриваться как постоянная.

x								y4										1			1			1			47
x	3		3	dy (x		3		y4		x				2				1			1		4	1		4	47		4
		y					y		) \|1		x				x				x			x			x			x		.
		y					y	4	) \|1		x				x			2	x		4	x		16	x		64	x		.
1								4		2	x							2			4			16			64
2 x
Далее вычислим внешний интеграл
				4						47			x5			4	47			45
				47 x4dx						47			x5				47			45		752 .
				47 x4dx						64							64			5		752 .
				0	64					64		5				0	64			5		5
				0

Задание 12. Вычислить площадь фигуры, ограниченной линией

2 a2 sin 2 .

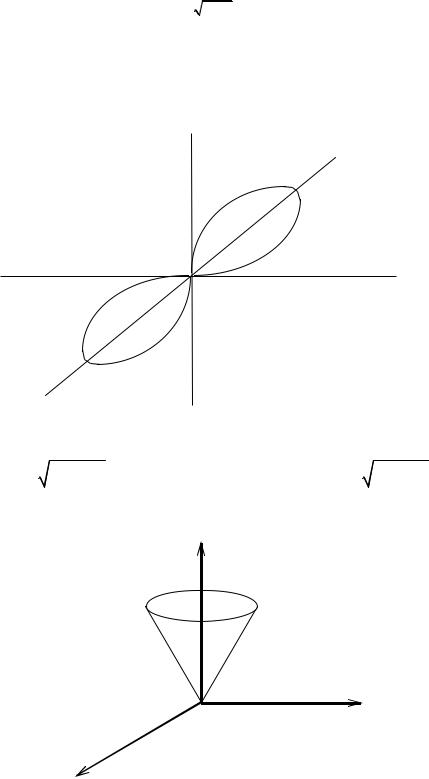
Решение. Построив кривую и замечая, что она симметрична относительно полюса и что при изменении от 0 до 2 текущая точка ( , ) отсечет половину кривой, расположенную выше полярной оси, будем иметь:

		a	sin 2
		a	sin 2	d a2 2 sin 2 d
S d d 22 d				d a2 2 sin 2 d
D	0		0		0
	a2				a2.
		cos 2		2
		cos 2		2
	2			0
				0

					2 a2 sin 2

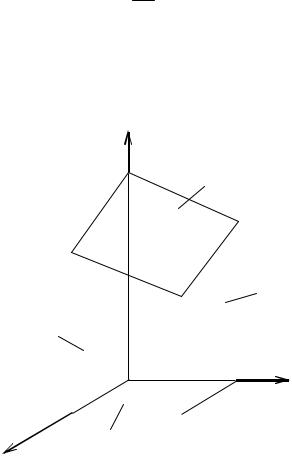
Задание 13. Найти массу тела, ограниченного поверхностями z 0,

x2 y2 R2 ,	z	x2 y2 , если плотность тела равна	x2 y2 .
Решение.
		z

2	R		2	R		2	R	R4	2
m d d dz d					d dz d 3d				d
								4
0	0	0	0	0	0	0	0		0

R4 2 R4 . 4 2

Задание 14. Найти центр тяжести однородной усеченной призмы, ограниченной координатными плоскостями и плоскостями x y z 4,

x 1, y 1.

x+y+z=4

					y=1
					y=1
	x=1
	x=1
		D		C	y
		D		C
	A
x			B
x		x=1
		x=1

Построив данные плоскости, замечаем, что ограниченная ими усеченная призма симметрична относительно плоскости x y . Вследствие этого

xc yc .

Для однородного вертикального цилиндрического тела (с образующей, параллельной оси OZ), имеющего своим основанием область D на плоско-

сти XOY и ограниченного поверхностью

z f x, y , координаты центра

тяжести выражаются формулами:

xzdxdy

M yz

; y

yzdxdy

z2dxdy

M xy

;

xdxdy

zdxdy

xdxdy

M yz xzdxdy

x 4 x y dxdy xdx 4 x y d

4 x y

OABC

	1	4 x y 2							1						1	0			3								1 2					3			7		2					17
		4 x y 2							1						1	2x			3	7x dx							1 2					3			7		2					17
					2				0 xdx						2									2						3 x					2 x						12 .
					2										2									2						3 x					2 x						12 .
	0															1
																					1				1
M xy z2dxdy									4 x y 2dxdy dx 4 x y 2d 4 x y
	D							OABC													0				0
					1		4 x y							3	dx 13				0	3 x 3 4 x 3 dx
							4 x y
									3
									3
					0														1																				.
										1	x 3 4									x 4 4								55.											.


										3					4					4									6
										3					4					4									6

									1			1											1		1
		m zdxdy dx												4 x y dy											4 x y 2													dx
																																						dx
																							2
					D				0			0											2		0
					D				0			0													0
				1																	x					3			3	x					4	3
			1	3			x 2 4 x 2 dx 1																																	3.
			1	3			x 2 4 x 2 dx 1																																	3.
			2	0																2				3									3
			2																	2				3									3

						x		y					M yz				17		,		z	c					M xy					55			.
						x		y											,		z														.
						c			c					m			36											m				36
														m			36											m				36
Задание 15.						Вычислить									J xydx x2									y dy,									если линия L – дуга
																		L
параболы y = x2, расположенная между точками A (0, 0) и B (2, 4).
Решение. Из y = x2 следует dy 2xdx,																					x				0,2 . Откуда
																b

	P x, y dx Q x, y dy																	P x, f x Q x, f x f																					x dx
	P x, y dx Q x, y dy																	P x, f x Q x, f x f																					x dx
L																a
					2																2
			x x2 x2 x2														2x dx 5x3dx														5 x		4	2	20.
			x x2 x2 x2														2x dx 5x3dx														5 x		4	2	20.
					0																0										4			0
																															4			0

Задание				16.				Проверить,										является									ли				заданное											выражение
4x x2 y2 dx 4 y x2 y2 dy															полным дифференциалом функции u x, y ,
и найти u x, y . Сделать проверку.
Решение. Имеем: P 4x x2 y2 , Q 4 y x2																														y2 .

<<< < Предыдущая 1 2 3 4 56 / 106 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.06.2024177.48 Кб074.pdf
#
16.06.2024674.16 Кб0740.pdf
#
16.06.2024674.3 Кб0741.pdf
#
16.06.2024674.54 Кб0742.pdf
#
16.06.2024676.7 Кб0743.pdf
#
16.06.2024679.39 Кб3744.pdf
#
16.06.2024680.06 Кб0745.pdf
#
16.06.2024680.5 Кб0746.pdf
#
16.06.2024681.69 Кб0747.pdf
#
16.06.2024685.43 Кб0748.pdf
#
16.06.2024686.32 Кб0749.pdf