
744
.pdf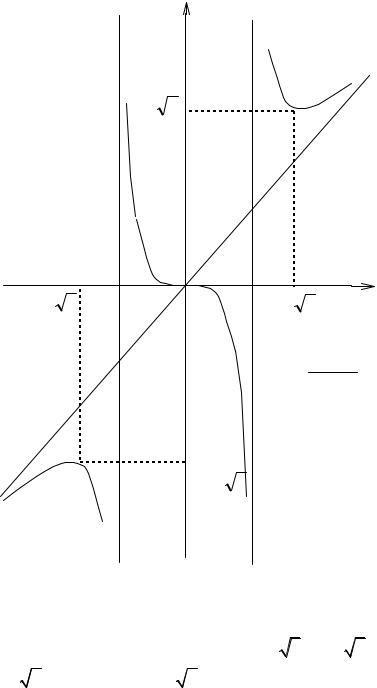
|
|
|
|
y |
|
|
|
|
|
|
3 |
3 |
|
B |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
3 |
-1 |
|
|
1 |
|
3 |
|
|
|
|
|
|
y |
|
x3 |
|
|
|
|
|
|
|
|
x2 1 |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Рис.9 |
|
|
|
|
Функция возрастает на интервалах ( ; |
3 ) |
и ( 3; ) и убывает на |
||||||
интервалах 3; 1 , |
1;1 и (1; |
3 ). |
|
|
|
|
||
4) Интервалы выпуклости, вогнутости. Точки перегиба. |
||||||||
Найдем вторую производную и приравняем ее к нулю: |
||||||||
|
x 3x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
4 |
|
|
2 |
|
|
|
4x |
3 |
6x x |
2 |
1 |
|
|
2 x |
2 |
1 |
2x x |
4 |
3x |
2 |
|
|
|||||||
f x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||
x |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
x |
2 |
1 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x x2 1 2x2 3 x2 1 2 x4 3x2 |
|
2x x2 3 |
0. |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x2 1 |
|
|
|
|
|
|
||
41

Следовательно, x = 0 – возможная точка перегиба. |
||||
Укажем интервалы выпуклости и вогнутости. |
||||
Знак f x |
|
|
|
|
– |
+ |
– |
+ |
x |
|
-1 |
|
0 |
1 |
выпукл. вогн. выпукл. вогн.
Точка 0 (0, 0) – точка перегиба графика функции. Интервалы выпуклости: ( ;1) и (0,1).
Интервалы вогнутости: (–1, 0) и (1, + ). 5) Наклонные асимптоты.
Найдем
|
|
k lim |
f x |
lim |
|
|
x2 |
|
|
|
1, |
|
|
|
|||
|
|
x |
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
|
x x2 1 |
|
|
|
|
|
||||||||
b |
lim |
f x kx |
lim |
|
x |
3 |
|
|
x |
|
|
lim |
x |
0 |
|||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||
|
x |
|
x x2 1 |
|
|
|
|
|
x x2 1 |
|
|||||||
Таким образом, у данной кривой существует одна наклонная асимптота y = x.
График функции приводится на рис.9.
Задание 12. Найти производную и градиент скалярного поля
u x2 y2 z ln z 1 |
в |
точке |
M (1; 1; 2) |
по |
направлению |
вектора |
||||||||||||||||||||||||||
|
|
5 |
|
|
|
6 |
|
|
|
|
2 5 |
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||
l |
i |
|
j |
k |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Решение |
|
|
|
|
|
|
|
|
u x, y, z по |
|
|
|||||||||||||||||||
|
|
Производная скалярного |
поля |
направлению |
вектора |
|||||||||||||||||||||||||||
|
|
l1 |
|
l2 |
|
|
l3 |
|
|
|
вычисляем по формуле |
|
|
|
||||||||||||||||||
l |
i |
j |
k |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
u cos |
u cos u cos , |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
x |
|
|
|
y |
z |
|
|
|
где cos |
|
l1 |
|
; |
cos l2 |
; cos l3 |
являются |
координатами единичного |
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
l |
|
l |
|
l |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
вектора |
|
|
|
|
|
|
l2 |
l2 l2 . |
|
|
|
|
|
|
|
|||||||||||||||||
l |
,а |
|
l |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
|
|
|
|
|
|
|
|||||||||||
Найдем длину вектора l .
l 52 62 2 5 2 25 36 20 81 9.
42
Тогда cos 5 |
; |
cos 2 ; |
cos |
2 |
5 |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
9 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Частные производные функции u x, y, z в точке M (1; 1; 2) имеют зна- |
|||||||||||||||||||||||||||||||||||||
чения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
u |
|
|
M 2xy |
2 |
z |
|
|
|
|
|
2 1 1 2 4; |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
M |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
2x2 yz |
|
M 2 1 1 2 4; |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
u |
|
y |
|
M |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
0; |
|
|
||||||||
|
|
|
x |
|
|
|
|
|
z 1 |
|
|
|
2 1 |
|
|
||||||||||||||||||||||
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Подставляя в формулу, найдем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
u |
|
|
|
4 |
5 |
|
|
|
|
2 |
|
|
|
2 5 |
4 |
5 |
|
2 |
|
4 |
. |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
l |
|
|
|
|
|
|
|
|
4 |
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
M |
|
|
|
9 |
|
|
|
|
3 |
|
|
|
|
|
9 |
|
|
9 |
|
|
3 |
|
9 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Градиент скалярного поля u x, y, z есть вектор gradu , направленный
по нормали к поверхности у ровня в сторону возрастания поля. Вычисляем по формуле
gradu ux i uy j uz k
Подставляя значения частных производных в последнюю формулу, получим:
gradu 4i 4 j .
Задание 13. Проверить, удовлетворяет ли уравнению
x2 2u 2xy 2u y2 2u 0x2 xdy y2
функция u xey x .
x .
Решение
Найдем все производные второго порядка от функции u xey x :
x :
u |
e |
y x |
xe |
y x |
|
y |
e |
y x |
|
y |
e |
y x x y |
|
||||
|
|
|
|
|
|
1 |
|
|
|
|
, |
||||||
x |
|
x |
2 |
|
|
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||||
u xey x 1 ey
x 1 ey x ,
x ,
y x
43

2u |
e |
y x |
|
|
y |
|
|
x y |
e |
y x |
|
x x y |
e |
y x y2 |
||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||||||||||
x |
|
|
x |
2 |
|
|
x |
|
|
|
|
x |
2 |
|
|
|
|
|
x |
3 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2u |
e |
y x 1 |
|
|
|
ey x |
|
2u |
e |
y x |
|
|
y |
|
|
yey x |
|
|
||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||
y |
|
|
|
x |
|
x |
x y |
|
|
|
|
x |
2 |
|
|
x |
2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Подставим найденные производные в уравнение |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
y x y2 |
|
|
|
|
|
|
yey x |
|
|
|
2 ey x |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
x |
e |
|
|
|
|
|
|
|
|
2xy |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
x2 |
|
|
x2 |
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
eyx x y2 2 y2 y2 0.
x y2 2 y2 y2 0.
Получилитождество, иследовательно, функцияудовлетворяетуравнению.
Задание 14. Найти экстремум функции z x |
y x2 |
y 6x 3. |
|||||||
|
Решение |
|
|
|
|
|
|
||
Найдем частные производные: |
z |
y 2x 6, |
z |
|
|
x |
1. |
||
y |
2 |
y |
|||||||
|
x |
|
|
|
|
||||
Приравнивая эти производные к нулю, получим систему уравнений, из которой определяются стационарные точки данной функции:
|
|
y 2x 6 0 |
||||
|
|
x |
|
|
|
|
|
|
|
|
1 |
0. |
|
|
|
|
|
|||
2 |
|
y |
||||
|
|
|
|
|
||
Из второго уравнения:
y 2x
Подставим это выражение в первое уравнение, получим: 2x 2x 6 0; x 4x 12 0;
3x 12; x 4; y 22 4.
Таким образом, имеем одну стационарную точку M (4; 4). Проверим ее на экстремум с помощью достаточных условий. Для этого найдем сначала вторые частные производные:
2 z |
|
1 |
; |
2 z |
|
x |
; |
2 z |
2. |
|
xdy |
2 y |
y2 |
4 y y |
x2 |
||||||
|
|
|
|
|
Подставим координаты стационарной точки:
2 z |
|
2; |
2 z |
|
|
1 |
|
1 |
; |
2 z |
|
4 |
|
|
1 |
. |
|
|
|
||||||||||||||
x2 |
|
x y |
|
2 4 |
4 |
y2 |
4 4 |
4 |
8 |
|||||||
|
M |
|
M |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44
Подсчитаем
|
2 z |
|
|
2 z |
|
|
2 z |
|
|
2 |
|
|
|
1 |
|
1 2 |
|
||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
x |
|
y |
|
x y |
8 |
4 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
M |
|
|
|
M |
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
1 |
|
3 |
0. |
|
|
|
16 |
|
|||||||
|
2 z |
|
|
|
4 |
16 |
|
|||
Величина 0 и |
|
0 |
, следовательно, в точке M (4; 4) функция |
|||||||
x2 |
|
|||||||||
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеет максимум. Подсчитаем максимальное значение функции: |
||||||||||
z 4;4 4 4 42 4 6 4 3 8 16 1 24 15; zmax 15 в точке M (4; 4).
Задание 15. Найти наибольшее и наименьшее значения функции
zx2 2xy 52 y2 2x
вобласти D, ограниченной прямыми x = 0; y = 0; x = 2; y = 2.
Решение
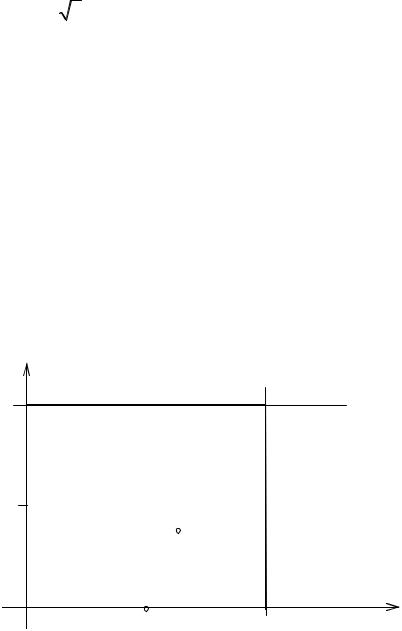
Изобразим область D. Она представляет собой квадрат (рис.11). Най-
дем стационарные точки, лежащие внутри квадрата:
z 2x 2 y 2;
x
|
z |
2x 5y. |
|
y |
y |
|
|
|
|
|
|
C |
y=2 |
B |
|
1 |
|
x=2 |
M1 |
x=0
|
|
M2 |
|
A |
x |
0 |
|
|
|
|
|
y=0 1 |
2 |
|
|
||
Рис.11
45

Приравнивая производные к нулю, получим систему
x y 12x 5y;
y x 1, |
x |
2 x 1 0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
5 |
|
5 |
|
|
2 |
|
|
x, |
x 1 x |
; y |
1 |
|
. |
||||||
y |
5 |
5 |
3 |
3 |
3 |
|||||||
|
|
|
|
|
|
|
|
|||||
Как видим, стационарная точка M1 ( 53 ; 23 ) лежит внутри квадрата. Подсчитаем значение функции в этой точке:
z M1 |
|
5 2 |
2 |
5 |
|
2 |
|
5 |
|
2 2 |
2 |
5 |
|
||
|
3 |
|
3 |
3 |
2 |
|
3 |
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|
||||||
25 |
20 |
10 |
10 |
5 |
20 |
15. |
|||
9 |
9 |
9 |
3 |
9 |
9 |
9 |
|||
Затем найдем наибольшее и наименьшее значения функции на сторо- |
|||||||||
нах квадрата: |
|
|
|
|
|
|
|
|
|
1) сторона ОA: y = 0; 0 x 2 |
|
|
|
|
|
|
|||
|
|
z z x x2 2x. |
|
||||||
На концах интервала z |
|
O z 0 |
0; z |
|
A z 2 0. Стационарные точ- |
||||
|
|
||||||||
ки найдем из уравнения z |
|
x 0 : |
|
|
|
|
|
|
|
z x 2x 2 0; |
x 1; |
M2 1;0 . |
|||||||
Подсчитаем значение функции в этой точке: z M2 z 1 1 2 1.
2) Сторона AB: x = 2; 0 y 2.;
z z y 4 4 y 52 y2 4 52 y2 4 y.
На концах интервала z B z 2 52 4 8 2. Найдем стационарные точки:
z y 5y 4 |
0; y |
4 |
; M3 |
|
2; |
4 |
|
5 |
|
5 |
. |
||||
|
|
|
|
|
|
46

Подсчитаем значение функции в точке M3: |
|
|
|
||||||||||||||
z |
|
M3 |
5 |
|
4 |
2 |
|
4 |
|
8 |
|
16 |
|
8 |
|
||
|
|
|
|
|
|
||||||||||||
|
2 |
|
5 |
|
4 |
|
5 |
|
5 |
|
5 |
|
5 |
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||
3) Сторона BC: y = 2; 0 x 2; |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
z z x x2 |
6x 10. |
|
|
|
||||||||||
На концах интервала |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
z |
|
C z 0 |
10. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
Найдем стационарные точки: |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
z z x 2x 6; |
x 3 |
0,2 |
|
||||||||||||
4) Сторона ОC: x = 0; 0 y 2; |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
z z y 5 y2. |
|
|
|
|
||||||||
2
Найдем стационарные точки:
z y 5y 0; y 0.
Получили граничную точку.
Из всех найденных значений функции z выбираем наибольшее и наименьшее значения:
zmax 10 в точке С(0; 2); |
|
|
|
||||
z |
min |
15 в точке M |
|
5 ; |
2 |
. |
|
|
9 |
1 |
3 |
3 |
|
|
|
|
|
|
|
|
|||
Задание 16. Найти уравнения касательной плоскости и нормали к по- |
|||||||
верхности 2x2 y2 2z2 |
xy xz 3 |
в точке M0 1;2;1 . |
|||||
Решение
Найдем частные производные:
Fx 4x y z ; Fy 2 y x;
Fz 4z x;
вычислим их в точке M0 :
Fx M0 4 1 2 1 7 ;
47
|
|
|
|
|
|
|
Fy |
|
M0 |
2 2 1 3 ; |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
Fz |
|
M0 |
4 1 1 5. |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Подставим в уравнение касательной плоскости: |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
Fx |
|
M0 x x0 Fy |
|
M0 y y0 Fz |
|
M0 z z0 0; |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
7 x 1 3 y 2 5 z 1 0, |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
7x 3y 5z 6 0 |
|
|
|
|
|
||||||||||||||||||||||||
и в уравнение нормали: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x |
|
x0 |
|
|
y |
|
y0 |
|
z |
|
z0 |
, |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
Fx |
|
|
Fy |
|
|
|
Fz |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
M0 |
|
|
M0 |
|
|
|
M0 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
x 1 |
|
y 2 |
|
|
z 1 |
. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Задание |
17. Найти |
формулу |
|
вида |
y ax b |
методом |
наименьших |
||||||||||||||||||||||||||||||
квадратов по данным таблицы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
5 |
|
||||||||
|
y |
|
5,9 |
6,9 |
|
|
|
5,4 |
|
|
|
|
|
|
3,4 |
|
3,9 |
|
|||||||||||||||||||
Решение
Найдем коэффициенты a и b путем минимизации суммы
S a,b yi axi b 2 .
i 1
По данным таблицы составим систему двух линейных уравнений
|
|
|
|
yi xi a xi |
2 |
b xi 0 |
|
i 1 |
i 1 |
|
i 1 |
|
|
|
|
yi a xi bn 0, |
|||
i 1 |
i 1 |
|
|
решив которую найдем параметры a и b. Предварительно вычислим суммы:
5
xi yi 5,9 13,8 16,2 13,6 19,5 69;
i 1
5
xi2 1 4 9 16 25 55;
i 1
48
|
|
5 |
|
|
|
|
|
xi 1 2 3 4 5 15; |
|
||
|
|
i 1 |
|
|
|
|
5 |
|
|
|
|
yi 5,9 6,9 5,4 3,4 3,9 25,5. |
|
||||
|
i 1 |
|
|
|
|
Составим систему уравнений: |
|
|
|
||
|
|
55a 15b 69 |
|
|
|
|
|
3a b 5,1 b 5,1 3a, |
|
||
|
|
55a 76,5 45a 69, |
|
||
|
|
10a 7,5 a 0,75, |
|
||
|
|
b 5,1 2,25 7,35; |
|
||
Искомая формула имеет вид: |
|
|
|
||
|
|
y 0,75x 7,35 |
|
||
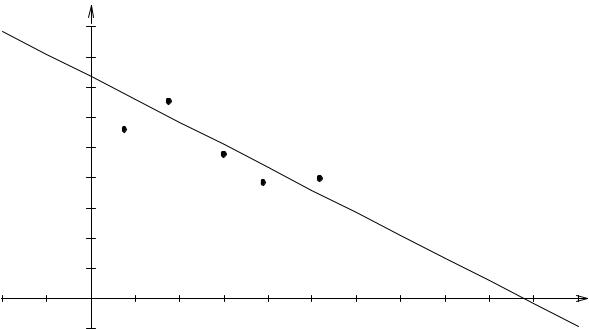
График искомой зависимости приводится на рис.12. |
|
||||
y |
|
|
|
|
|
9 |
|
|
|
|
|
8 |
|
|
|
|
|
7 |
|
|
|
|
|
6 |
|
|
|
|
|
5 |
|
|
|
|
|
4 |
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
x |
0 |
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
9,8 |
-1 |
|
|
|
|
|
|
|
|
Рис.12 |
|
|
|
|
|
49 |
|
|
Элементы теории функций комплексного переменного. Неопределенный и определенный интеграл.
Кратные и криволинейные интегралы
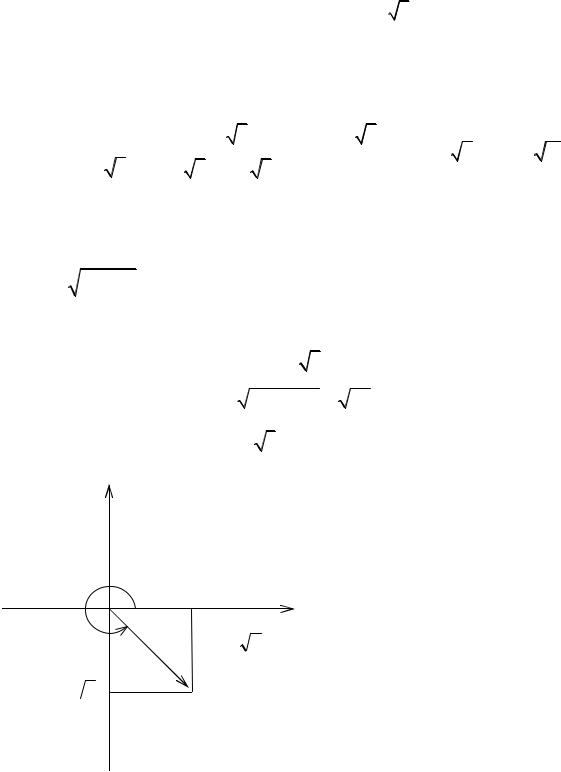
Задание 1. Дано комплексное число z |
|
|
16 |
. |
|
|
|
|
|
|
|||||||||||||||
1 |
i 3 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Записать число в алгебраической, тригонометрической и показатель- |
|||||||||||||||||||||||||
ной формах. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Запишем число z в алгебраической форме: |
|
|
|
|
|
|
|||||||||||||||||||
z |
16 |
|
|
|
16 1 i 3 |
|
|
16 1 i |
|
|
3 |
4 1 i |
3 4 4 3i. |
||||||||||||
1 i 3 |
1 i 3 1 i 3 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
1 3 |
|
|
|
|
|
|
|
|
|
||||||||||
В тригонометрической форме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
z r cos isin , |
|
|
|
|
|
|
|
||||||||||||
где r |
x2 y2 , |
x r cos , y r sin ; |
r |
– |
модуль комплексного |
числа. |
|||||||||||||||||||
При этом tg |
y |
|
– главные значения |
0 2 |
аргумента комплексного |
||||||||||||||||||||
x |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
числа. В данном случае x = 4, |
y 4 3 ; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
r |
16 16 3 |
64 8. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
tg 3; |
2 |
|
5 . |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
Тригонометрическая |
|
форма |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
числа будет |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 8 |
cos |
5 |
isin |
5 |
. |
||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
||
|
|
|
|
|
4 |
|
|
|
|
|
Показательная |
форма |
ком- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
плексного числа |
|
|
|
|
|
||||||||
|
|
|
|
|
|
z 4 4 |
3i |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
i |
. |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z r ei 8e 3 |
|
|||||||
4 3
3
50
