
744
.pdf8) Найти lim x sin 5x ctg2 2x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
sin5x ~ 5x |
|
tg2x ~ 2x |
|||||||||
Заменим |
эквивалентные |
|
величины |
|
и |
|||||||||||||||||||
при x 0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim x sin5x ctg2 2x lim |
xsin5x |
lim |
|
|
5x2 |
|
5 . |
|
|||||||||||||||
|
|
tg2 2x |
2x 2 |
|
||||||||||||||||||||
|
x 0 |
|
|
|
x 0 |
|
|
x 0 |
|
4 |
|
|||||||||||||
9) lim 3x 5 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x 2; |
Сделаем |
предварительно |
замену |
|
переменной. |
|
Обозначим |
||||||||||||||||||
y 0 при x 2 . Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x 2 |
3x 5 |
|
x |
y 0 |
|
|
y 2 |
|
|
|
|
y 2 |
|
|
|
|
|||||
|
|
|
|
3 |
5 |
y |
|
|
||||||||||||||||
|
|
|
x 2 |
|
|
|||||||||||||||||||
|
|
|
lim |
|
lim |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
3y 1 |
|
1 |
e3 2 e6. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
y |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приведем и другой способ вычисления. А именно, при вычислении пределов выражений вида uv, где u x 1 и v x при данном пре-
дельном переходе, удобно пользоваться формулой limuv elim vln u .
Так как в данном случае u 3x 5 |
и v |
|
|
x |
|
при x 2 , то, поль- |
|||||||||
|
x 2 |
||||||||||||||
зуясь последней формулой, получим |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
x |
lim |
x |
ln 3x 5 |
|
|
lim |
y 2 |
|
|
||||
|
|
|
|
|
|
||||||||||
|
3x 5 |
|
|
|
|
|
y |
ln 3 y 1 |
|
||||||
lim |
|
ex 2 x 2 |
|
|
ey 0 |
|
|
||||||||
x 2 |
|
|
|
||||||||||||
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
y 2 |
3 y |
|
|
lim 3 y 2 |
|
|
|
|
|
|||
|
|
|
|
|
e6. |
|
|
||||||||
|
ey 0 |
y |
ey 0 |
|
|
|
|
||||||||
10) lim x 3 ln x 5 ln x 2 .
x
Запишем разность логарифмов как логарифм частного и, выделив целую часть дроби, заменим эквивалентные величины:
ln 1 ~ при 0 .
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
x 3 |
|
ln |
|
x 5 |
|
ln |
|
x 3 |
|
lim |
|
x 3 |
|
ln |
x 5 |
|
|||||||||
x 3 |
|||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
lim |
x |
3 ln 1 |
|
|
|
|
|
|
lim |
x |
3 |
|
|
|
2. |
|
||||||||||
|
x 3 |
x |
3 |
|
|||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||
31

Задание 4. Определить число точек разрыва функции f (x) x x 51 x 3
Решение.
Точками разрыва будут точки, в которых функция не существует, то есть нули знаменателя.
x x 5 x 3 0 x 0 или x 5 , или x 3
Ответ: 3
1
Задание 5. Дана функция f x 153 x и два значения аргумента x1 = 3
и x2 = 1. Требуется: 1)найти предел функции при приближении к каждому из заданных значений слева и справа; 2) установить, является ли данная функция непрерывной или разрывной для каждого из заданных значений x; 3) сделать чертеж.
Решение
1
Функция f x 153 x в точке x = 3 не определена. Найдем в этой точке левый и правый односторонние пределы.
1
|
|
|
|
lim 15 |
|
|
|
15 ; |
|
|
|
|||||
|
|
|
|
|
3 x |
|
|
|
||||||||
|
|
|
|
x 3 o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3 3 x 0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
15 |
|
1 |
|
0. |
|||||
|
|
|
|
lim 15 |
3 x |
|
|
|||||||||
|
|
|
|
15 |
||||||||||||
|
|
|
|
x 3 o |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x 3 3 x 0 |
|
|
|
|
|
|
|
|||||
В точке x1 |
= 3 |
функ- |
|
|
|
|
y |
|
|
|
|
1 |
|
|||
ция терпит бесконечный |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
y 15 |
3 x |
|
|||||
разрыв. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В точке x2 = 1 функ- |
|
|
|
|
|
|
|
|
|
|
|
|
||||
ция непрерывна: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
15 |
|
|
|
|
|
|
|
||||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
lim15 |
3 x |
152 |
15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Сделаем |
схематиче- |
|
|
|
|
|
|
|
|
|
|
|
x |
|||
ский чертеж (рис.7). |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
||
Рис.7
32
Задание 6. Функция задается различными аналитическими выражениями для различных областей изменения независимой переменной
x 2, |
где |
x 1; |
|
где |
1 x 1; |
f x x2 1, |
||
x 3, |
где x 1. |
|
|
|
|
Требуется:
1)найти точки разрыва функции, если они существуют;
2)найти скачок функции в каждой точке разрыва;
3)сделать схематический чертеж.
Решение
Данная функция определена при всех значениях x. Разрыв она может иметь в точках x = –1 и x = 1. Найдем односторонние пределы в этих точках.
lim |
f x |
lim |
x 2 1 2 1; |
||
x 1 0 |
|
x 1 0 |
|
|
|
x 1 |
|
|
|
|
|
lim |
f x |
lim |
|
x2 |
1 1 1 2 . |
x 1 0 |
x 1 0 |
|
|
||
x 1 |
|
|
|
|
|
Так как lim f x |
lim |
f x , то функция f x в точке x = –1 терпит |
|||
x 1 0 |
x 1 0 |
|
|
|
|
конечный разрыв. |
|
|
|
|
|
Скачок функции в этой точке равен |
f x 2 1 1; |
||||
|
lim f x |
lim |
|||
x 1 0 |
x 1 0 |
|
|||
Найдем односторонние пределы функции в точке x = 1.
lim |
f x |
lim |
f x2 |
1 1 1 2; |
|
x 1 0 |
|
x 1 0 |
|
|
|
x 1 |
|
|
|
|
|
lim |
f x |
lim f x 3 1 3 2. |
|||
x 1 0 |
x 1 0 |
|
|
||
x 1 |
|
|
|
|
|
Так как lim f |
x |
lim f x |
2 , |
то функция f x в точке |
|
x 1 0 |
|
x 1 0 |
|
|
|
x = 1 непрерывна.
Сделаем схематический чертеж (рис.8).
33
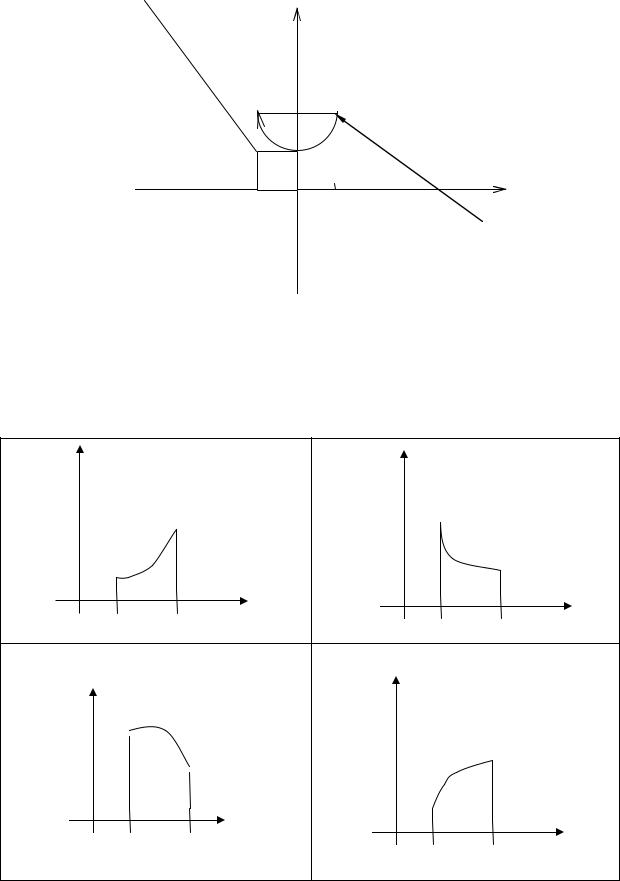
y
|
2 |
|
|
1 |
x |
|
|
|
-1 0 |
1 |
3 |
Рис.8
Задание 7. Графики каких из функций одновременно удовлетворяют |
|||
трем условиям: y 0, |
y 0, |
y 0 на всем отрезке a; b ? |
|
1) Все графики; |
2) Только IV; 3) Только III и IV; 4) Только II. |
||
I. y |
|
II. |
y |
|
|
|
|
0 |
а |
b |
x |
0 |
а |
b |
x |
|
|
||||||
|
|
|
|
||||
|
|
|
|
|
|
||
III. |
|
|
|
IV. |
|
|
|
|
|
|
|
y |
|
|
|
|
y |
|
|
|
|
|
|
0 |
а |
b |
x |
0 |
|
|
x |
|
|
а |
b |
||||
|
|
|
|
|
|
34

Решение.
Первоеусловие(y > 0) определяетположениекривойотносительноосиОУ. Поусловиюy > 0, следовательно, графикфункцииулежитвышеосиОУ. Второе условие ( y 0 ) показывает, возрастает или убывает функция
на данном промежутке. По условию y 0 , следовательно, функция воз-
растает на интервале.
Третье условие y 0 позволяет определить форму графика функции. По условию y 0 , следовательно, функция выпукла на данном интервале.
Всем трем условиям удовлетворяет только график на рис. IV. Ответ: Только IV.
Задание 8. Найти производные |
dy |
данных функций: |
|||||
|
|
4 |
|
|
dx |
|
|
а) |
y 5 3x2 4x 5 |
|
; |
|
б) |
y cos5 3x tg 4x 1 3 ; |
|
x |
4 4 |
|
|||||
|
|
|
|
|
|
||
в) |
y x 5 2 arccos3 5x4; |
|
|
|
г) |
y sin 3x arcctgx ; |
|
д) y2 x ln y .x
Решение
При решении указанных примеров используются следующие правила дифференцирования:
1)c 0, c const;
2)x 1, x – независимая переменная;
3)u v u v , где u u x ; v v x ;
4)u v u v v u;
5)c u c u ;
6)u u v 2 v u v 0 ;v v
|
7) если y f (u) , u u(x) , то есть |
y f u(x) |
– сложная функция, со- |
||
ставленная |
из дифференцируемых |
функций, |
то ux yu ux или |
||
dy |
dy |
du . |
Кроме этого используется таблица производных элементар- |
||
dx |
du |
dx |
|
|
|
ных функций:
1) u u 1 u ;
35
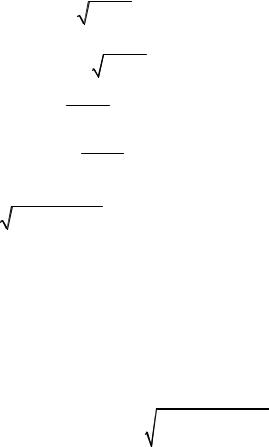
2)au au ln a u ;
3)eu eu u ;
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|||||
4) |
loga u |
|
|
|
|
|
|
|
|
|
|
; |
|
|
||||
|
u ln a |
|
|
|||||||||||||||
|
|
|
|
|
u |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5) |
ln u |
u |
; |
|
|
|
|
|
|
|
|
|
|
|||||
6) |
sin u cosu u ; |
|
|
|||||||||||||||
7) |
|
|
|
sin u u ; |
|
|
||||||||||||
cosu |
|
|
||||||||||||||||
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|||||
8) |
tgu |
|
|
|
|
|
; |
|
|
|
|
|
|
|||||
cos2 u |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|||
9) |
ctgu |
|
|
|
|
|
|
|
; |
|
|
|||||||
|
sin2 u |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
||||
10) |
arcsin u |
|
|
|
|
; |
|
|||||||||||
|
1 u2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
||
11) |
arccosu |
|
|
|
|
|
; |
|||||||||||
|
|
|
1 u2 |
|||||||||||||||
12)arctgu 1 uu2 ;
13)acctgu 1 uu2 .
а) |
y 5 3x2 4x 5 |
|
|
4 |
|
. |
|
|
|
|
|
|
|
|
x 4 4 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
3x |
2 |
4x 5 |
5 |
|
4 |
x 4 4 |
|
|
|||
|
y |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3x |
2 |
4x 5 |
|
4 |
3x |
2 |
|
|
4 4 x 4 |
5 |
x |
|
|
|
||||
|
5 |
|
|
5 |
|
4x 5 |
|
4 |
|
|
||||||||||
|
|
|
|
|
|
|
|
6x 4 |
|
|
|
16 |
. |
|
|
|
|
|
||
|
|
|
|
|
|
|
3x2 4x 5 4 |
|
x 4 5 |
|
|
|
|
|
||||||
|
|
|
|
55 |
|
|
|
|
|
|
|
|
||||||||
б) y cos5 3x tg 4x 1 3 |
|
|
|
|
cos5 3x tg 4x 1 3 |
|
|
|||||||||||||
|
|
y cos5 3x tg 4x 1 3 |
|
|
||||||||||||||||
36

5cos4 3x sin3x 3 tg 4x 1 3 cos5 3x |
|
3 4x 1 2 |
4 |
|
|||||||||||||||
cos2 4x 1 3 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
15cos4 3xsin3x tg 4x 1 3 |
|
12 4x 1 2 cos5 3x |
. |
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
cos2 4x 1 3 |
|
|
|
|||||||
в) y x 5 2 arccos3 5x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
3 |
4 |
2 |
2 |
|
4 |
|
20x3 |
|
|
|
|||||
y |
|
2 x |
5 arccos |
|
5x x 5 3arccos |
5x |
|
|
|
|
|
|
|
||||||
|
|
|
|
1 25x8 |
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
2 |
x 5 arccos3 5x4 |
|
60x3 x 5 2 arccos2 5x4 |
. |
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
1 25x8 |
|
|
|
|
|
|
|
|
|||
г) y sin 3x arcctgx .
Это показательно-степенная функция. Прологарифмируем ее: ln y arcctgxln sin 3x
и затем продифференцируем обе части полученного равенства:
|
y |
|
ln sin3x |
arcctg x cos3x 3 |
|
ln sin3x |
3ctg3xarcctg x. |
||||||||
|
y |
|
|
|
|
|
|||||||||
|
|
|
|
1 x2 |
|
|
sin3x |
|
1 x2 |
|
|
||||
Отсюда выразим y : |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
y |
(sin 3x) |
arcctgx |
|
|
3ln(sin3x) |
|||||
|
|
|
|
|
3ctg3xarcctgx |
1 x |
2 |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
y |
|
|
|
|
|
|
|
|
|||
д) |
y |
|
|
x ln |
|
. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||
Это неявно заданная функция. Продифференцируем по x обе части уравнения:
2 yy 1 y1x y x 2 y ; x
2xy2 y xy y x y .
Разрешим полученное равенство относительно производной y : y 2xy2 x xy y;
y |
y x 1 |
|
|
. |
|
x(2 y2 1) |
||
37
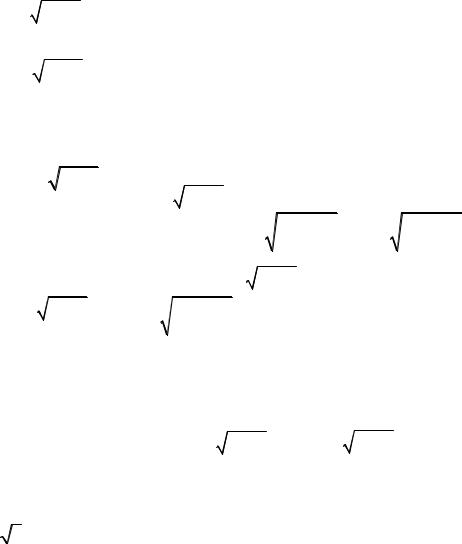
Задание 9. Найти |
dy |
, |
d 2 y |
для функций. |
|
dx |
dx2 |
||||
|
|
Решение |
|||
а) y x 1 e3x2 5 . |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x2 5 |
|
x 1 e |
3x2 5 |
|
|
|
|
|
|
3 x2 5 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y |
e |
|
6x e |
1 6x |
|
6x , |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y e3x2 5 6x(6x2 6x 1) e3x2 5 12x 6 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3x2 5 |
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x2 5 |
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
6e |
|
|
6x |
|
6x |
|
|
x 2x 1 6e |
|
|
6x |
6x |
3x 1 . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
x |
|
|
|
t2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
t 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
t2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
y |
|
|
|
|
d 2 y |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx |
t ; |
|||||||||||
Это параметрическая функция, для которой: |
|
|
|
|
|
|
|
|
|
t |
|
|
|
и |
|
dx2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
dx |
|
|
xt |
|
|
|
xt |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
t2 1 t 1 |
|
|
|
2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
yt |
2 t2 1 |
t2 1 2t2 2t |
|
|
|
|
|
t 1 |
|
|
; |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
t2 1 |
|
|
|
|
|
|
|
|
|
|
t2 1 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
xt |
|
|
t |
|
|
|
|
; |
|
dy |
|
|
|
|
|
t 1 |
|
|
|
|
t2 1 |
|
|
|
t |
1 |
|
|
|
|
|
|
1 |
|
|
; |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
t |
|
|
|
|
|
t |
2 |
1 t |
|
t t |
1 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
t2 1 |
|
|
|
|
|
|
|
t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2t 1 |
|
|
|
|
|
2t 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
t |
|
|
|
t2 t |
2 |
t2 t 1 |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
t |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 y |
|
|
|
2t 1 |
|
|
|
|
|
t2 1 |
2t 1 |
|
|
t2 1 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx2 |
|
t2 t 1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
t3 t 1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Задание |
|
10. |
|
|
Найти наибольшее |
и |
наименьшее |
|
|
значения функции |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
f x |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
cos x на отрезке 0; |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ; ). Найдем |
|
критические |
|
точки |
||||||||||||||||||||||||||||||||||||
Область |
|
определения |
|
функции |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
f x sin x 0, |
|
|
x n. При n = 0 x = 0 |
|
|
|
|
|
|
. Это единственная кри- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
0; |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
38

тическая точка на данном интервале. Вычислим значения функции в критической точке и на концах отрезка:
|
f 0 |
|
|
3 |
|
1 |
3 2 |
; |
f |
|
3 |
. |
|||||||
|
|
2 |
|
|
2 |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||
Выбираем среди найденных значений функции наименьшее и наи- |
|||||||||||||||||||
большее: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||
|
|
|
min |
f x f |
|
|
|
|
|
; |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
0; |
|
|
|
2 |
|
2 |
|
|
|
|
|
|||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
max |
|
|
f x f 0 |
|
3 2 |
|
|
|||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x 0; |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Задание 11. Исследовать методами дифференциального исчисления |
|||||||||||||||||||
функцию f x |
x3 |
|
и построить ее график. |
|
|
|
|
|
|||||||||||
x2 1 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение
Исследуем функцию по следующей схеме:
1) Областьопределения. Точкиразрыва. Вертикальныеасимптоты.
Функция теряет смысл, если знаменатель обращается в нуль ( x2 1 0 ). Следовательно, x 1 – точки бесконечного разрыва:
lim |
|
|
x3 |
|
|
lim |
|
|
x3 |
|
; |
|||||
|
|
|
|
|
|
|
x 1 x 1 |
|||||||||
x 1 0 x2 1 |
|
x 1 0 |
|
|
||||||||||||
x 1 |
|
|
|
|
|
|
|
x 1 0 |
|
|
|
|
|
|
||
lim |
|
|
x3 |
|
|
|
lim |
|
|
x3 |
; |
|||||
|
x2 1 |
|
|
|
x 1 x 1 |
|||||||||||
x 1 0 |
|
|
|
x 1 0 |
|
|
|
|||||||||
x 1 |
|
|
|
|
|
|
|
x 1 0 |
|
|
|
|
|
|||
lim |
|
|
|
x3 |
|
|
lim |
|
|
x3 |
|
; |
||||
|
x2 1 |
x 1 x 1 |
||||||||||||||
x 1 0 |
|
|
x 1 0 |
|
||||||||||||
x 1 |
|
|
|
|
|
|
|
x 1 0 |
|
|
|
|
|
|
||
lim |
|
|
x3 |
|
|
lim |
|
|
x3 |
|
; |
|||||
x2 1 |
x 1 x 1 |
|||||||||||||||
x 1 0 |
|
|
x 1 0 |
|
||||||||||||
x 1 |
|
|
|
|
|
|
|
x 1 0 |
|
|
|
|
|
|
||
Данная кривая имеет две вертикальные асимптоты: x = –1 и x = 1.
2) Корни функции. Интервалы знакопостоянства. Четность, нечетность.
39
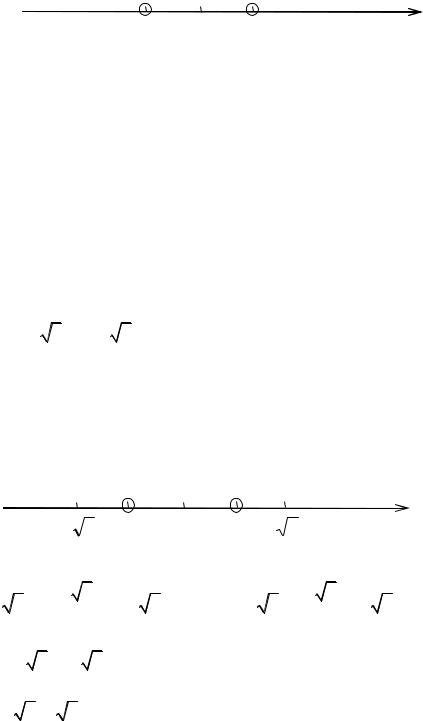
Найдем точки, в которых функция обращается в нуль: f x |
x3 |
|
0 |
|
x2 1 |
||||
|
|
|||
при x = 0.
Точка пересечения с осью абсцисс 0 (0, 0). Укажем интервалы знакопостоянства функции.
Знак f x
– |
+ |
– |
+ |
|
x |
|||
|
-1 |
0 |
|
1 |
|
|
||
f x |
|
x3 |
|
|
x3 |
|
f x . |
|
x 2 1 |
x2 1 |
|||||||
|
|
|
||||||
Следовательно, функция нечетная и ее график симметричен относительно начала координат 0 (0, 0).
3) Интервалы возрастания, убывания. Экстремумы.
Найдем первую производную и приравняем ее к нулю:
|
|
3x2 |
|
x2 1 x3 2x |
|
x2 |
|
3x2 3 2x2 |
|
|
x2 |
|
x2 3 |
|
|
||||||||||
f x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0; |
|||||
|
|
|
x2 |
|
|
2 |
|
|
|
x2 |
|
2 |
|
|
x2 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
||||||
x1 0, x2 |
|
3, x3 |
|
|
3 – стационарные точки. |
|
|
|
|
|
|
|
|
|
|||||||||||
Определим вид экстремума и интервалы возрастания и убывания функции.
Знак f x
|
|
|
max |
|
|
min |
|
|
|
|
|
|
||||
|
|
+ |
|
|
– |
|
– |
– – |
+ |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
-1 |
0 |
1 |
3 |
|
|
|
|
|
Вычислим функцию в точках экстремума |
|
|
|
|
|
|
||||||||||
f |
|
|
3 |
3 |
|
3 |
|
f 3 |
|
3 |
3 |
|
3 |
|
||
3 |
|
3 1 |
2 |
3 2,55, |
3 1 |
|
2 |
3 2,55. |
||||||||
|
|
3; |
|
3 |
3 |
|
точка максимума. |
|
|
|
|
|
|
|||
Точка A |
2 |
– |
|
|
|
|
|
|
||||||||
|
|
3; 3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Точка B ( |
|
|
3 ) – точка минимума (рис.10). |
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40
