744

В качестве точки M1 x1, y1, z1 , через которую проходит искомая пря-

мая, можно взять точку ее пересечения с любой из координатных плоскостей, например, с плоскостью YOZ . Так как при этом x1 0 , то координа-

ты y1 и z1 этой точки определятся из системы уравнений, состоящей из уравнений заданных плоскостей, если в них принять x 0 :

2 y z 6 0,y z 1 0.

Решив эту систему, найдем y1 5, z1 4 .

Так что, искомая прямая определится уравнениями:

x y 5 z 4 1 3 5

или

x t,

y 5 3t, z 4 5t.

21

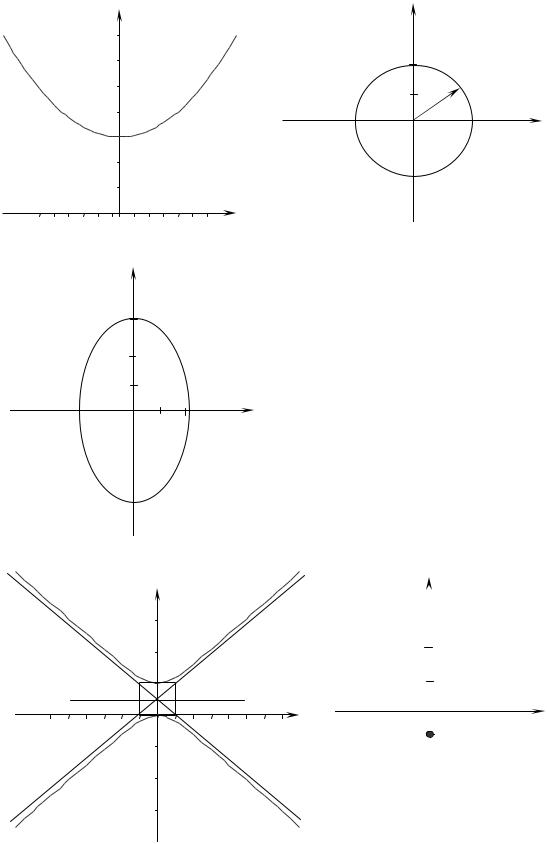
Задание 14. Установить вид кривых, заданных уравнениями. Привести уравнения кривых к каноническому виду и изобразить их на чертеже

Решение

а) х2 – 16у + 48 = 0 х2 = 16(у – 3) – парабола; б) х2 + у2 – 4 = 0 х2 + у2 = 4 – окружность (1);

22

Рис. 4 (к задаче14)

23

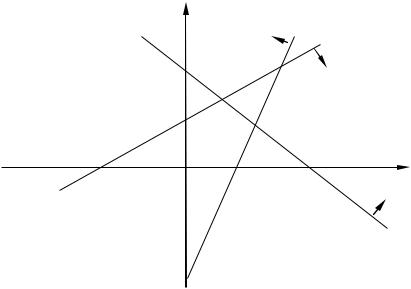
Задание 15. Построить на плоскости область решений системы линейных неравенств

2x y 83x 5y 30

2x 4 y 12.

-8

Рис.5 (к задаче № 15)

Ответ: областью решений является множество точек плоскости, ограниченное треугольником ABC.

Задание 16. Записать уравнение линии 2x2 2 y2 72 в полярных ко-

ординатах.

Решение.

Имеем x cos , y sin . Тогда исходное уравнение примет вид: 2 2 cos2 2 2 sin2 72 ,

2 2 cos2 sin2 72 ,

2 2 72 ,

2 36 . Так как 0 , то уравнение примет вид 6 .

Ответ: 6 .

24

Задание 17. Линия задана уравнением

4

r2 3cos

вполярной системе координат. Требуется: 1) построить линию по точкам,

начиная от = 0 до = 2 и придавая значения через промежуток 8 ;

2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось – с полярной осью; 3) по уравнению в декартовой системе координат определить, какая это линия.

Решение

Составим таблицу значений функции.

В силу симметрии функции cos значения функции от = до = 2 повторяются в обратном порядке

Найдем уравнение линии в декартовой прямоугольной системе координат.

25

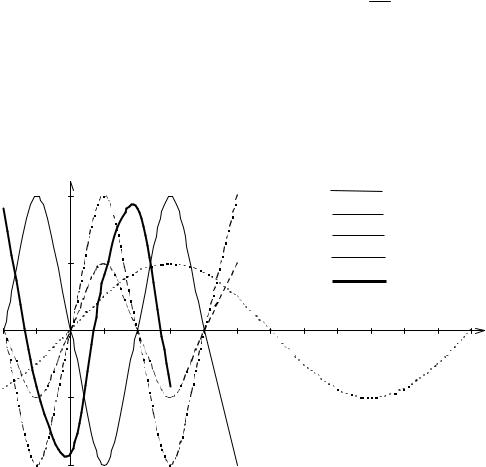
Решение

От функции y sin x к функции y 2sin 3x 2 можно перейти с помощью следующей цепочки преобразований:

y sin x,

y1 sin 3x, y2 2sin 3x,

y3 2sin 3x 2 .

Геометрически это приводит к следующим построениям (рис.6): 1) Построим одну волну синусоиды y sin x .

2) График функции y1 sin3x получается сжатием предыдущего гра-

фика в три раза, так как период этой функции T 23 .

3) График функции y2 2sin3x получается из графика y1 sin3x растяжениемв2 разавдольосиOy иотражениемполученногографикаотосиOx.

Рис.6

Задание 4. Найти указанные пределы, не пользуясь правилом Лопиталя.

1) Найти lim 4x33 3x2 1 . x 2 3x 3x 1

Точка x = 2 принадлежит области определения функции.

28

Воспользуемся тем, что для всех основных элементарных функций в

2) Найти lim x6 6 3x2 2 . x 2x 4x 5

В данном случае имеем неопределенность . В подобного рода при-

мерах пользуются утверждением: многочлен при x эквивалентен своему старшему члену

При подстановке предельного значения аргумента получим неопределенность 00 , которая разрешается сокращением дроби на разность x – 2.

Для чего квадратные трехчлены, стоящие в числителе и в знаменателе, разложим по формуле

ax2 bx c a x x1 x x2 ,

где x1 и x2 – корни квадратного трехчлена:

29

сопряженное числителю, другое – знаменателю. После этого сократим дробь надвучлен(x – 4):

7) Найти lim1 cos 4x .

x 0

Используем формулу 2sin2 x 1 cos2x , а затем – эквивалентность величин sin 2x ~ 2x при x 0 :

30