Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

744

.pdf

Скачиваний:

Добавлен:

16.06.2024

Размер:

679.39 Кб

Скачать

☆

<<< < Предыдущая 12 / 102 3 4 5 6 7 8 9 10 > Следующая >>>

x1 1 2 1;1

x2 2 31 3;

x3 3 1 1.1

Ответ: в базисе a,b, c x = (1, -3, 1).

Задание 5. Дана система линейных уравнений

x1 2x2 3x3 62x1 3x2 4x3 203x1 2x2 5x3 6

Доказать ее совместность и решить двумя способами:

1) методом Гаусса; 2) средствами матричного исчисления.

						Решение
Вычислим определитель системы
				1	2			3
				1	2			3
				2		3	4		58 0.
				3	2		5
Следовательно, система совместна.
1) Решение системы методом Гаусса
1		2	3		6		1			2	3	6


			4								10



	2	3			20			0 7				8


	3	2	5		6			0 4			14	12

1	2	3		6	1	2	3	6


0	1 10 / 7			8 / 7	0	1	10 / 7	8 / 7 .






0	0	58 / 7	116 / 7		0	0	1	2




Откуда
x3 2;
x2 10 / 7x3 8 / 7,				x2 8 / 7 10 / 7 2 4;
x1 2x2 3x3 6,				x1 6 2 4 3 2 3 2 8.
Ответ: x1 8,	x2 4, x3 2..

2) Решение системы средствами матричного исчисления. Запишемсистемуввидематричногоуравнения, введятриматрицы:

1		2	3		6			x1
A	2	3	4	;	B	20	;	x x	2	.
	3	2	5			6			2
	3	2	5			6		x
									3

A x B x A 1 B.

Найдем обратную матрицу A 1 . Определитель матрицы A:

1 2 3

A	2	3 4 58 0.

3		2	5

Следовательно, матрица A невырожденная и обратная матрица A 1 существует:

A 1 1A A* ,

где A* – присоединенная матрица. Запишем транспонированную матрицу

	1	2	3
T	2	3	2
A	2	3	2
	3	4	5
	3	4	5

и каждый ее элемент заменим его алгебраическим дополнением. Получим присоединенную матрицу

	3		2			2		2				2		3
	3		2			2		2				2		3
	4		5			3		5					3 4
	4		5			3		5					3 4					23		16	1

	2		3				1 3						1 2
*	2		3				1 3						1 2						2	14	10
A	4		5				3 5						3	4					2	14	10	.
	4		5				3 5						3	4					13	4	7
		2	3		1				3				1	2					13	4	7
		2	3		1				3				1	2
		3	2										2 3
		3	2		2			2					2 3
					2			2
								1	23				16			1
				A	1			1			2		14
															10			.
								58							10			.
								58		13			4				7
										13			4				7

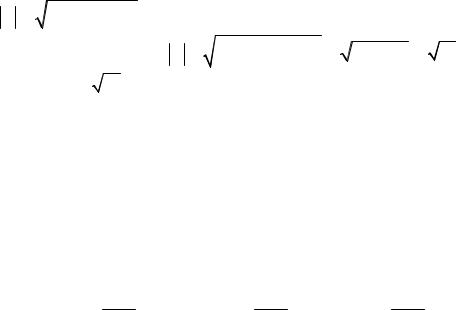
Найдем матрицу X:
x1					1	23								16					1										6						1					138												320								6
x					1					2				14					10										20						1								12									280						60
x										2				14					10										20														12									280						60
2				58					13						4					7									6														78											80				42
x				58					13						4					7									6						58								78											80				42
3
																				1					464											8
																				1
																												232								4			.
																												232								4			.
																				58								116								2
																												116								2
Откуда x1 8,								x2 4, x3 2.
Задание 6. Найти c 2a 3																								, если									a 3									2												и									3				7				.
																					b																															k					b													k
																					b																		i							j						k					b				i					j				k
Решение.
2a 2 3		2							6					4				2								; 3					3							3							7								3						9						21				.
						k																k								b																				k																		k
	i			j		k					i					j						k								b						i								j						k								i						j				k
Тогда вектор																											) 3																					9
c 2a 3										(6				4				2																9							21															13						23					.
							b																k																								k																			k
							b					i				j							k										i					j									k								i					j						k
Ответ:		9		13						23					.
Ответ:		9	i	13				j		23			k		.
Задание 7. Найти длину																	a			вектора												a												3							.
Задание 7. Найти длину																	a			вектора												a					i						j	3					k		.
Решение.

Если вектор задан своими координатами a a1,a2 ,a3 (разложен по единичным векторам), то его модуль или длина находятся по формуле:

a a12 a22 a32 .

a 12 12 3 2 1 1 9 11 .

Ответ: 11.

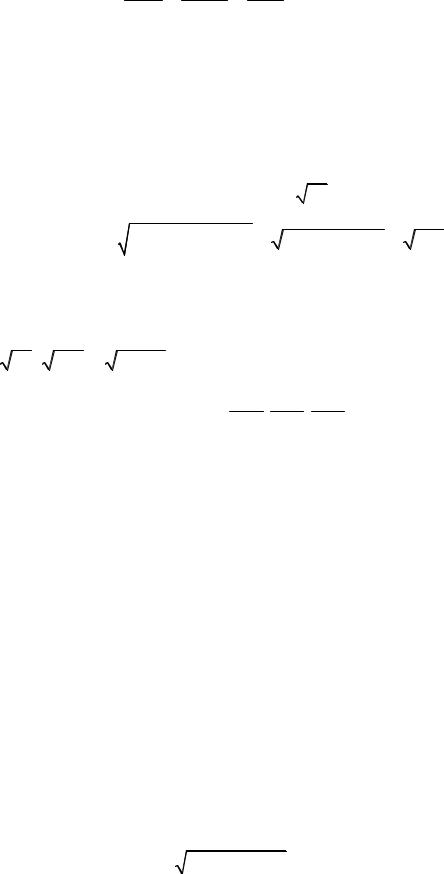
Задание 8. Даны координаты вершин пирамиды A1 (10, 6, 6); A2 (–2, 8, 2);

A3(6, 8, 9); A4 (7, 10, 3). Найти: 1) длины ребер A1A2, A1A3, A1A4; 2) косинус угла между ребрами A1A2 и A1A4; 3) площадь грани A1A2A3; 4) уравнения прямой A1A2; 5) уравнение плоскости A1A2A3; 6) уравнения высоты, опущенной из вершины A4 на грань A1A2A3; 7) угол между ребром A1A4 и гранью A1A2A3; 8) объем пирамиды (двумя способами). Сделать чертеж.

Решение

1) Имеем:

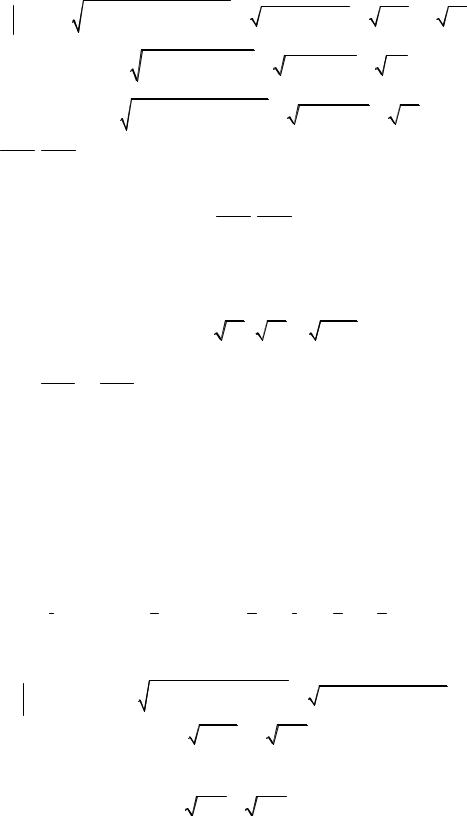
A1A2 = (–12, 2, –4); A1A3 = (–4, 2, 3); A1A4 = (–3, 4, –3),

					12 2 22			4 2	144 4 16		164 2 41,
A A					12 2 22			4 2	144 4 16		164 2 41,
1	2
							4 2 22 32			16 4 9		29,
				A A			4 2 22 32			16 4 9		29,
					1	3
							3 2	42 3 2		9 16 9		34.
			A A				3 2	42 3 2		9 16 9		34.
		1			4

2) A1A2 , A1A4 12 3 2 4 4 3 36 8 12 56

Угол между ребрами равен углу между векторами:

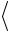А1А2 , А1А4 .

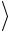Тогда


				,
cos		A1A2		,	A1A4				56		28	0,7499.
	A A					A A		2	41	34	1394


	1		2			1	4

3) Площадь грани A1A2A3 равна площади треугольника, построенного на векторах A1A2 и A1A3 :

						S A1A2 A3				1


										2	A1A2 , A1A3								.
										2	A1A2 , A1A3								.
Найдем векторное произведение															,			:
Найдем векторное произведение													A A		,	A A		:
														1 2 1 3

					i		j		k			2		4				12		4		12	2
					i		j		k
		,		12		2		4
	A A		A A
	A A		A A							i							j				k
1 2		1 3		4		2		3				2		3				4		3		4	2
												2		3				4		3		4	2

6 8 i 36 16 j 24 8 k 14i 52 j 16k 14,52, 16 .

Модуль векторного произведения:

						16	2
	, A1A3	14	2	52	2			196 2704 256

A1A2

3156 2 789.

Откуда искомая площадь:

S A1A2 A3		1	2	789	789 28,089	ед.2 .
		2

4) Уравнения прямой A1A2 определяется как уравнения прямой, проходящей через две данные точки:

	x x1			y y1					z z1					,
														,
	x		x	y	2		y		z	2	z
2			1		2		1			2			1
			x 10			y 6			z 6				,
		2 10				8 6			2 6				,
		2 10				8 6			2 6
			x 10		y 6			z 6				,
			12									,
			12				2		4
или			x 10		y 6			z 6
			x 10		y 6			z 6				,
			6									,
			6				1		2

5) Уравнение плоскости A1A2A3 запишем как уравнение плоскости, проходящей через три данные точки:

x x1 x2 x1 x3 x1

y y1 y2 y1 y3 y1

z z1

z2 z1 0; z3 z1


	x 10		y 6		z 6			x 10		y 6		z 6
	x 10		y 6		z 6			x 10		y 6		z 6
	2 10		8 6		2 6	0;		12		2		4	0;
	6 10		8 6		9 6			4		2	3
x 10		2	4	y 6			12	4	z 6			12	2	0 ;
x 10		2	4	y 6			12	4	z 6			12	2	0 ;
		2	3				4	3				4	2

x 10 6 8 y 6 36 16 z 6 24 8 0; 14 x 10 52 y 6 16 z 6 0;

14x 52 y 16z 356 0;

Следовательно, искомое уравнение плоскости A1A2A3: 7x 26 y 8z 178 0 –

6) Уравнения высоты из точки A4 на грань A1A2A3 определится как уравнения прямой, проходящей через точку A4 перпендикулярно плоскости

A1A2A3:

x x0	y y0	z z0	.
l	m
		n

За направляющий вектор a l,m,n примем нормальный вектор плоскости A1A2A3:

n 7,26, 8 .

Тогда уравнения высоты запишутся в виде:

x 7 y 10 z 3. 7 26 8

7)Угол между ребром A1A4 и гранью A1A2A3 – это угол между прямой

иплоскостью, составляющий в сумме с углом между направляющим вектором прямой и нормальным вектором плоскости прямой угол.

Следовательно,

					sin			a	,	n	.
											.
								a		n
								a		n
		a				3,4, 3 ,						a	34,
				A1A4
				A1A4
n 7, 26, 8 ,			n		72 262 8 2								49 676 64	789;
n 7, 26, 8 ,			n		72 262 8 2								49 676 64	789;
a,n 3 7 4 26 3 8 21 104 24 107 .
Откуда	107				107
	107				107
sin							0,6533 ( arcsin 0,6533							39 20 ) .
sin	34 789				26826		0,6533 ( arcsin 0,6533							39 20 ) .
8) Объем пирамиды A1A2 A3 A4							равен, с одной стороны, одной шестой мо-

дуля смешанного произведения векторов A1A2 , A1A3, A1A4 , с другой стороны – одной третьей произведения площади S основания A1A2A3 на высоту H, опущенную на основание из вершины A4.

Так что:									x1			y1		z1						12 2				4
						1											1

				V					x		y		2	z	2					4 2				3
				пир			6		2				2		2		6				3	4		3
									x		y			z							3	4		3
									3				3		3
				1				2		3				2		4		3			4		4	2
				1				2		3						4		3					4	2
				6	12			4		3						3	3						3	4
								4		3						3	3						3

	16 12 18 2 21 4 10																	1073 35 32							ед.3
Или	V	1 S	A A A				H .
	пир	3	A A A
		3		1	2	3
				1	2	3
Высоту H найдем как расстояние от точки A4 (7, 10, 3) до плоскости
A1A2A3:
												Ax0 By0 Cz0 D
							H d					Ax0 By0 Cz0 D
							H d
														A2 B2					C2

7 7 26 10 8 3 178		49 260 24 178			107	,
72 262 8 2			789		789
Vпир 1 789	107	107	35 2	ед.3 .
3	789	3	3

						z
						A3
				9		A3
				9

			6
						A1			A2
			3			A1

					-2
								A4
		2									y
		2


							6	8		10
7	6						6	8		10

Рис.1 (к задаче № 8)

Задание 9. Найти величины отрезков (с учетом знаков), отсекаемых

прямой

2x y 8 0

на осях координат.

Решение.

Перейдем от общего уравнения прямой к уравнению в отрезках:

2x y 8;

;

Значит a 4,

b 8.

Ответ: a 4

b 8 .

Задание 10.

Какие

из заданных

плоскостей:

a) 4x 5y 3z 1 0;

b)2 y z 3 0;

c) 2x 5y 3z 0;

d) 7z 1 0 ; параллельны оси OX :

1) a) и c) ; 2) b) и d) ;

3) только d) ; 4) ни одна.

Решение.

Первая плоскость содержит все три переменные, поэтому пересекает все координатные оси.

Вуравнении второй плоскости отсутствует переменная х, так что она параллельна оси Ох.

Вуравнении третьей плоскости отсутствует свободное слагаемое; плоскость проходит через начало координат (не параллельна ни одной из осей).

Вуравнении четвертой плоскости содержатся лишь одна переменная z

исвободное слагаемое; плоскость проходит параллельно плоскости Oxy, а следовательно параллельна и оси Ох.

Ответ: 2) b) и d) .

Задание 11. Найти точку N, симметричную точке М (2, -5, 7) относительно прямой, проходящей через точки A (5, 4, 6) и B(–2,–17,–8).

Решение

Канонические уравнения прямой, проходящей через две заданные точки имеют вид:

	x x1				y y1						z z1				.
															.
	x	x		y			2	y			z	2	z
2		1					2	1				2	1
Для точек A и B будем иметь:
			x 5			y 4				z 6
			7
			7				21				14
или
		x 5			y 4				z 6					.
		1												.
		1						3			2

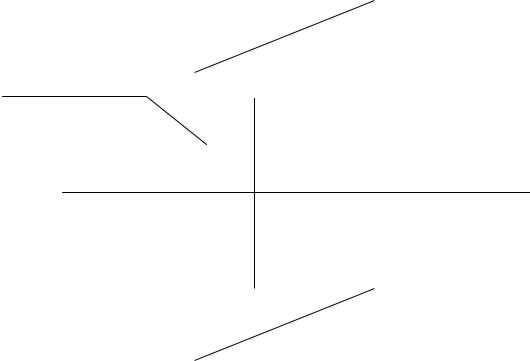
Уравнение плоскости, проектирующей точку М (2, –5, 7) на данную прямую (рис. 2), имеет вид:

A x 2 B y 5 C z 7 0 .

Координаты нормального вектора (A, B, C) плоскости, перпендикулярной прямой, заменим координатами направляющего вектора (1, 3, 2) данной прямой. Уравнение указанной плоскости будет иметь вид:

1 x 2 3 y 5 2 z 7 0

или

x 3y 2z 1 0 .

x 3y 2z 1 0

M 2, 5, 7

x 5

y 4

z 6

P 3, 2, 2

A 5, 4, 6

B 2, 17, 8

N 4,1, 3

Рис.2 (к задаче 11)

Параметрические уравнения прямой AB имеют вид: x t 5,

y 3t 4, z 2t 6.

Подставляя x,y,z в уравнение плоскости, найдем t=–2.

Отсюда x 2 5 3, y 6 4 2, z 4 6 2 , P (3,–2,2).

Координаты симметричной точки найдем, используя формулы для координат середины отрезка:

xN 2xP xM 2 3 2 4 , yN 2 yP yM 2 2 5 1,

zN 2zP zM 2 2 7 3 .

Ответ: N(4, 1, –3).

Задание 12. Составить параметрические уравнения прямой:

x 2 y z 6 0,2x y z 1 0.

Решение
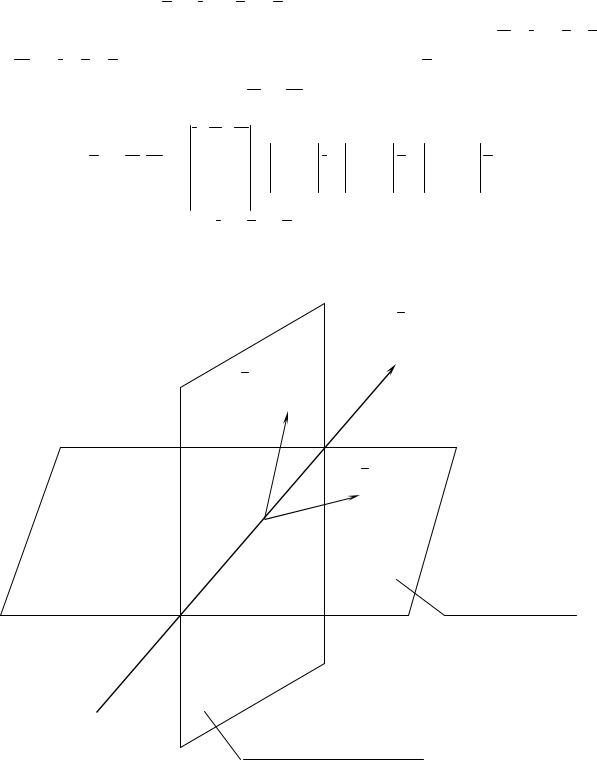
Найдем вектор		a l i m j nk ,				параллельный искомой прямой. Так
как он должен быть перпендикулярен нормальным векторам n1 i 2 j k
и n2 2i j k заданных плоскостей						(рис. 3), то за a можно принять век-
торное произведение векторов n1					и n2 :
		i	j	k	2 1 i 1			1 j 1		2 k
a n	,n	1 2 1			2 1 i 1			1 j 1		2 k
1	2				1	1	2 1		2 1
		2 1 1			1	1	2 1		2 1
			i 3 j 5k 1, 3, 5 .
Таким образом, l 1, m 3, n 5 .
									a 1, 3, 5
				n 1, 2, 1
								n 2, 1,1
										x 2 y z 6 0
				2x y z 1 0

Рис. 3 (к задаче 12)

<<< < Предыдущая 12 / 102 3 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.06.2024177.48 Кб074.pdf
#
16.06.2024674.16 Кб0740.pdf
#
16.06.2024674.3 Кб0741.pdf
#
16.06.2024674.54 Кб0742.pdf
#
16.06.2024676.7 Кб0743.pdf
#
16.06.2024679.39 Кб3744.pdf
#
16.06.2024680.06 Кб0745.pdf
#
16.06.2024680.5 Кб0746.pdf
#
16.06.2024681.69 Кб0747.pdf
#
16.06.2024685.43 Кб0748.pdf
#
16.06.2024686.32 Кб0749.pdf

	3		2			2		2				2		3
	3		2			2		2				2		3
	4		5			3		5					3 4
	4		5			3		5					3 4					23		16	1

	2		3				1 3						1 2
*	2		3				1 3						1 2						2	14	10
A	4		5				3 5						3	4					2	14	10	.
	4		5				3 5						3	4					13	4	7
		2	3		1				3				1	2					13	4	7
		2	3		1				3				1	2
		3	2										2 3
		3	2		2			2					2 3
					2			2
								1	23				16			1
				A	1			1			2		14
															10			.
								58							10			.
								58		13			4				7
										13			4				7

	3		2			2		2				2		3
	3		2			2		2				2		3
	4		5			3		5					3 4
	4		5			3		5					3 4					23		16	1

	2		3				1 3						1 2
*	2		3				1 3						1 2						2	14	10
A	4		5				3 5						3	4					2	14	10	.
	4		5				3 5						3	4					13	4	7
		2	3		1				3				1	2					13	4	7
		2	3		1				3				1	2
		3	2										2 3
		3	2		2			2					2 3
					2			2
								1	23				16			1
				A	1			1			2		14
															10			.
								58							10			.
								58		13			4				7
										13			4				7

	3		2			2		2				2		3
	3		2			2		2				2		3
	4		5			3		5					3 4
	4		5			3		5					3 4					23		16	1

	2		3				1 3						1 2
*	2		3				1 3						1 2						2	14	10
A	4		5				3 5						3	4					2	14	10	.
	4		5				3 5						3	4					13	4	7
		2	3		1				3				1	2					13	4	7
		2	3		1				3				1	2
		3	2										2 3
		3	2		2			2					2 3
					2			2
								1	23				16			1
				A	1			1			2		14
															10			.
								58							10			.
								58		13			4				7
										13			4				7