662

16.… – колеблемость, многообразие, изменяемость величины признака у единиц совокупности.

17.Абсолютная величина, характеризует группу единиц или всю совокупность.

20.Форма учета абсолютных величин. Денежные единицы.

23.Вид натуральных единиц. Имеют расчетные показатели, получаемые как произведение двух или нескольких показателей, имеющих простые единицы измерения. Например, учет затрат труда на предприятиях выражается в отработанных человеко-днях (число работников предприятия умножается на количество отработанных за период дней) или человеко-часах.

24.… интервала – разница между верхней и нижней границами.

25.Статистическая сводка, при которой производится группировка единиц наблюдения, подсчет итогов по каждой группе и по всей совокупности, и представление результатов группировки в виде статистических таблиц.

По вертикали

1.Если же сбор и обработка данных проводится в одном месте, то сводка называется …

2.Числовые значения количественного признака в ряду распределения, они могут быть положительными и отрицательными, абсолютными и относительными.

6.Вид группировки, позволяет выявить взаимосвязи между изучаемыми явлениями и их признаками (группировка банков по сумме уставного капитала, величине активов и балансовой прибыли).

10.Относительная величина... – представляет собой соотношение частей совокупности между собой.

12.Вид группировки, заключается в образовании новых групп на основе ранее произведенной группировки.

14.Множество единиц, обладающих массовостью, типичностью, качественной однородностью и наличием вариации, называется статистическая …

18.Статистические показатели по временному фактору, отражают состояние или уровень явления на определенный момент времени. Например, число вкладов в Сбербанке на конец какого-либо периода.

19.… величина – объем или размер изучаемого события или явления, процесса, выраженного в соответствующих единицах измерения в конкретных условиях места и времени.

21.Статистическая сводка, при которой производится подсчет общих итогов по изучаемой совокупности.

22.Показатель группировки, значение варьирующего признака, лежащее

вопределенных пределах. Нижняя граница интервала – это значение наименьшего признака в интервале. Верхняя граница – это наибольшее значение

винтервале.

22

4. Исчислите все возможные виды относительных величин.

Имеются данные о показателях деятельности Управление Росреестра

(табл. 2).

Таблица 2

Данные о деятельности Управления Росреестра

23

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4 СРЕДНИЕ ВЕЛИЧИНЫ

Средние величины делятся на два больших класса: степенные средние, структурные средние.

К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая.

В качестве структурных средних рассматриваются мода и медиана. Остановимся на степенных средних. Степенные средние в зависимости от

представления исходных данных могут быть простыми и взвешенными. Простая средняя считается по не сгруппированным данным и имеет следующий общий вид:

Взвешенная средняя считается по сгруппированным данным и имеет следующий общий вид:

где хi – варианты признака;

fi – частоты.

Пример. Имеется информация о площади 10 земельных участков, выделенных для строительства: 6; 10; 15; 6; 6; 10; 6; 15; 10; 15 га. Нам дан ряд одиночных значений признака, тогда среднюю площадь земельных участков

Построим ряд распределения (дискретный) земельных участков по площади.

24

В этом случае средний стаж работы будет определяться по средней арифметической взвешенной:

В случае интервальных рядов распределения расчет среднего значения признака ведется по формуле средней арифметической простой, но в качестве величины xi выступают середины интервалов.

Задания и упражнения

1.Вопросы для опроса (дискуссии):

Сущность и значение средних величин.

Виды средних величин и способы их вычисления.

Средняя арифметическая и ее свойства.

Средняя гармоническая и другие виды средних величин.

Структурные средние.

2. Определите среднюю урожайность.

Имеются данные об урожайности зерновых культур в фермерских хозяйствах (табл. 4).

Таблица 4

Данные об урожайности

3. Определить средний удельный показатель кадастровой стоимости земельных участков из состава земель населенных пунктов различных видов разрешенного использования.

25

Практическое занятие №5 ПОСТРОЕНИЕ СТАТИСТИЧЕСКИХ ГРАФИКОВ

Статистический график – это чертеж, на котором статистические совокупности, характеризуемые определенными показателями, описываются с помощью условных геометрических образов или знаков.

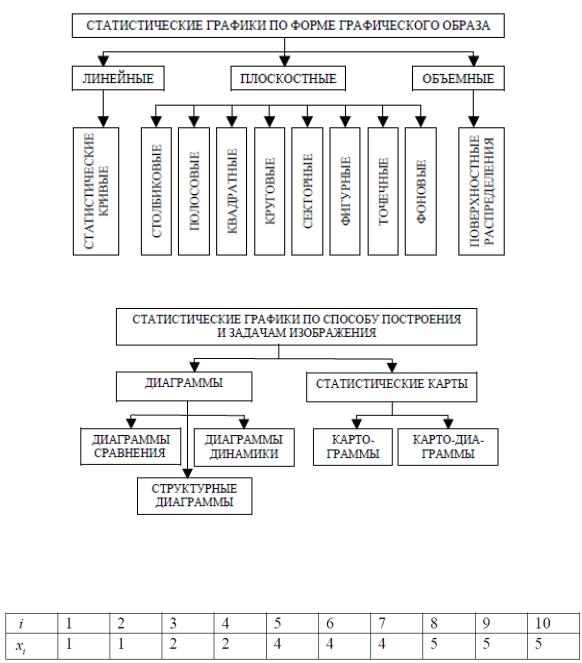
Рис. 2. Классификация статистических графиков по форме графического образа

Рис. 3. Классификация статистических графиков по способу построения и задачам изображения

Пример. Дан следующий вариационный ряд:

Требуется:

1)Построить полигон распределения.

2)Вычислить выборочную среднюю, дисперсию, моду, медиану.

3)Построить выборочную функцию распределения.

4)Найти несмещенные оценки математического ожидания и дисперсии.

27

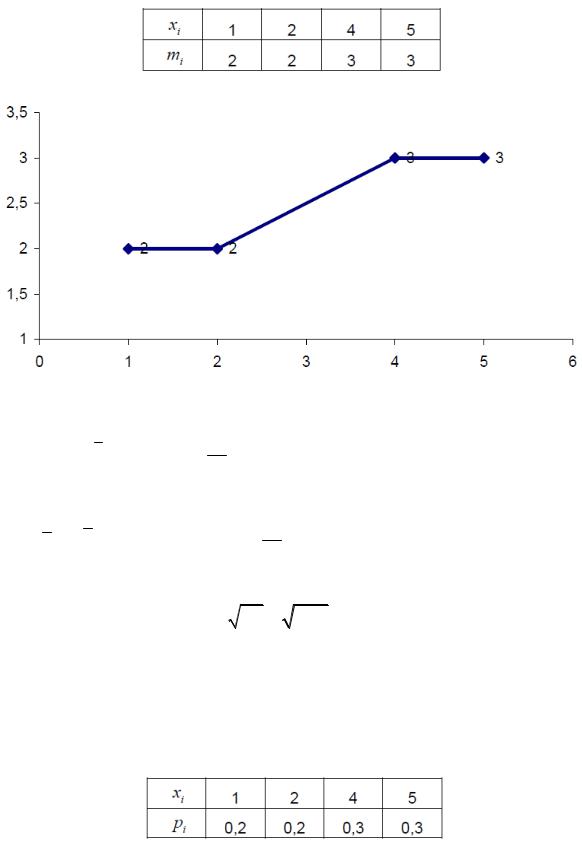
В задании дана выборка объема n =10.

1. Полигон распределения – это зависимость абсолютной частоты варианта mi от значения варианта xi. Эту зависимость можно представить в виде таблицы:

Строим график полигона частот:

2. Вычислим выборочную среднюю, дисперсию, моду, медиану. Выборочная средняя:

х 1n ximi 101 (1 2 2 2 4 3 5 3) 1033 3,3 .

Выборочная дисперсия:

Dx x2 (x)2 1n xi2mi 3,32 101 (1 2 4 2 16 3 25 3) 3,32 2,41.

Выборочное среднеквадратичное отклонение:

Модаравнаварианту, имеющемунаибольшуючастоту: xMo= 4; 5 (двемоды). Медиана равна среднему варианту выборки: xMe = 4.

3. Выборочная функция распределения аналогична функции распределения дискретной случайной величины. Для ее нахождения запишем ряд рас-

пределения выборки, где pi mni 10mi – относительная частота варианта хi.

28

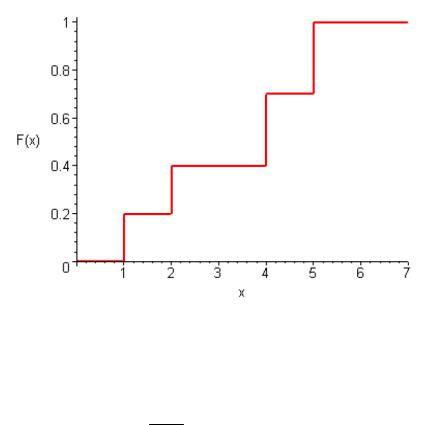
Тогда

0, x 1,

0, 2,1 x 2, F (x) 0, 4, 2 x 4,0, 7, 4 x 5,

1, x 5.

Построим график:

4. Несмещенная оценка математического ожидания совпадает с выборочной средней: M(X) = x = 3,3.

Несмещенная оценка дисперсии отличается от выборочной дисперсии в большую сторону:

D(X ) n n 1 Dx 109 2,41 2,678.

Задания и упражнения 1. Вопросы для опроса (дискуссии):

Значение графического метода в анализе статистических данных.

Элементы графика.

Классификация видов графика.

Диаграммы сравнения.

Структурные диаграммы.

Диаграммы динамики.

Статистические карты.

29

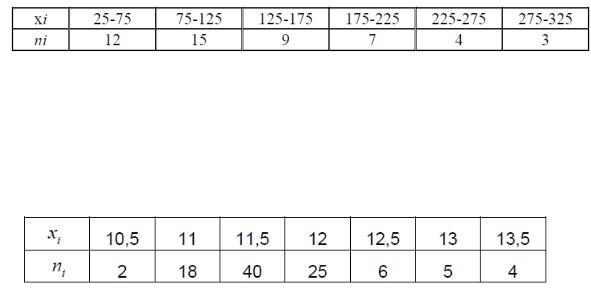
2. Проведено выборочное обследование сельскохозяйственных организаций. Имеются следующие данные о величине товарооборота для 50 сельскохозяйственных организаций (xi – товарооборот, млн руб.; ni – число сельскохозяйственных организаций).

Найти:

а) среднее X , среднее квадратическое отклонение S и коэффициент V; б) построить гистограмму и полигон частот.

3.Из генеральной совокупности извлечена выборка объема n. Найти выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную выборочную дисперсию, коэффициент вариации, моду и медиану.

4.Дана выборка10; 20; 20; 5; 15; 20; 5; 10; 20; 5. Требуется:

а) построить статистический ряд распределения частот и полигон частот; б) вариационный ряд; в) найти оценки математического ожидания и дисперсии;

г) найти выборочные моду, медиану, коэффициент вариации, коэффициент асимметрии.

30