650

декора для числа степеней свободы k1 n1 m и k2 n n1 m (m – чисE ло оцениваемых параметров в уравнении регрессии), т.е. Fрасч Fтабл . Чем больше величина Fрасч превышает табличное значение, тем больше

нарушена предпосылка о гомокедастичности.

Наличие гетерокедастичности в остатках регрессии можно проE верить и с помощью ранговой корреляции Спирмена. Суть проверки заключается в том, что в случае гетерокедастичности абсолютные остатки i коррелированы со значениями фактора xi . Эту корреляцию

можно измерить с помощью коэффициента ранговой корреляции Спирмена:

1 6 d 2 , n(n2 1)

где d – абсолютная разность между рангами xi и i . Статистическая значимость коэффициента оценивается по критерию Стьюдента. Расчетное значение tEкритерия вычисляется по формуле

Данная величина сравнивается с табличной величиной при 0,05 и числе степеней свободы n 2. Если t tтабл , то корреляция между i и xi статистически значима, т.е. имеет место гетерокедастичность

остатков. В противном случае принимается гипотеза об отсутствии гетерокедастичности остатков.

Проверку независимости последовательности остатков (отсутствие автокорреляции) осуществляют с помощью dEкритерия ДарбинаEУотE сона. Расчетное значение критерия определяется по формуле

di i 1 2

2i

исравнивается с нижним d1 и верхним d2 критическими значеE

ниями статистики ДарбинаEУотсона. Возможны следующие случаи:

1) Если d d1 , то гипотеза о независимости остатков отвергается, и

модель признается неадекватной по критерию независимости остатков. 2) Если d1 d d2 , включая сами эти значения, то считается, что

нет достаточных оснований делать тот или иной вывод.

21

3) Если d2 d 2 , то гипотеза о независимости остатков приниE

мается и модель признается адекватной по данному критерию.

4) Если d 2 , то это свидетельствует об отрицательной автокорреE ляции остатков. В этом случае расчетное значение критерия необхоE димо преобразовать по формуле d 4 d и сравнивать с критическим значением не d, а d .

При нарушении гомокедастичности и наличии автокорреляции ошибок рекомендуется заменять традиционный МНК обобщенным методом.

2.1.Суть метода наименьших квадратов состоит в

а) минимизации суммы остаточных величин; б) минимизации дисперсии результативного признака;

в) минимизации суммы квадратов остаточных величин.

2.2.Классический подход к оцениванию параметров регрессии осноB

ван на:

а) методе наименьших квадратов; б) методе максимального правдоподобия;

в) взвешенном методе наименьших квадратов.

2.3.Согласно методу наименьших квадратов минимизируется слеB дующее выражение:

2.4.Эффективность оценки параметра регрессии, полученной по методу наименьших квадратов, означает:

а) что она характеризуется наименьшей дисперсией; б) что математическое ожидание остатков равно нулю;

в) увеличение ее точности с увеличением объема выборки.

2.5.Состоятельность оценки параметра регрессии, полученной по методу наименьших квадратов, означает:

а) что она характеризуется наименьшей дисперсией; б) что математическое ожидание остатков равно нулю;

в) увеличение ее точности с увеличением объема выборки.

22

2.6. На основании наблюдений за 50 семьями построено уравнение регрессии y 284,56 0,672x , где y – потребление, x – доход. СоотB ветствуют ли знаки и значения коэффициентов регрессии теореB тическим представлениям?

а) да; б) нет;

в) ничего определенного сказать нельзя.

2.7. Суть коэффициента детерминации состоит в следующем:

а) оценивает качество модели из относительных отклонений по каждому наблюдению;

б) характеризует долю дисперсии результативного признака y , объясE няемую регрессией, в общей дисперсии результативного признака;

в) характеризует долю дисперсии y, вызванную влиянием не учтенных в модели факторов.

2.8.Качество модели из относительных отклонений регрессионного

ифактического значений признака по каждому наблюдению оценивает:

а) коэффициент детерминации; б) FEкритерий Фишера;

в) средняя ошибка аппроксимации A.

2.9.Какое значение не может принимать парный коэффициент корреляции:

а) E0,973; б) 0,005; в) 1,111; г) 0,721.

2.10.При каком значении линейного коэффициента корреляции связь между признаками можно считать тесной:

а) E0,975; б) 0,657; в) E0,111 г) 0,421.

2.11.Какой критерий используют для оценки значимости коэффиB циента парной корреляции:

а) FEкритерий Фишера; б) tEкритерий Стьюдента; в) критерий Пирсона;

г) критерий ДарбинаEУотсона.

23

2.12.Если парный коэффициент корреляции между признаками равен B1, то это означает:

а) отсутствие связи; б) наличие обратной корреляционной связи;

в) наличие прямой корреляционной связи; г) наличие обратной функциональной связи.

2.13.Если парный коэффициент корреляции между признаками принимает значение 0,675, то коэффициент детерминации равен:

а) 0,822; б) E0,675; в) 0,576; г) 0,456.

2.14.В уравнении парной линейной регрессии y a bx параметр b

означает:

а) усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов;

б) среднее изменение результативного признака при изменении факторного признака на 1 %;

в) на какую величину в среднем изменится результативный приE знак y, если переменную x увеличить на одну единицу измерения;

г) какая доля вариации результативного признака учтена в модели и обусловлена влиянием на нее переменной x?

2.15. В уравнении парной степенной регрессии y a xb параметр b

означает:

а) усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов;

б) среднее изменение результативного признака при изменении факторного признака на 1 %;

в) на какую величину в среднем изменится результативный приE знак y, если переменную x увеличить на одну единицу измерения;

г) какая доля вариации результативного признака учтена в модели и обусловлена влиянием на нее переменной x?

2.16. Значение параметра b в уравнении линейной регрессии y a bx определяется по формуле:

а) b y ax ;

б) b xy x y ; x2 x 2

24

2.17. Уравнение регрессии имеет вид y 2,02 0,78x . На сколько единиц своего измерения в среднем изменится y при увеличении x на

одну единицу своего измерения:

а) увеличится на 2,02; б) увеличится на 0,78; в) увеличится на 2,8; г) не изменится?

2.18.Какой критерий используют для оценки значимости уравнения регрессии:

а) FEкритерий Фишера; б) tEкритерий Стьюдента; в) критерий Пирсона;

г) критерий ДарбинаEУотсона.

2.19.Какой критерий используют для оценки значимости коэффиB циентов регрессии:

а) FEкритерий Фишера; б) tEкритерий Стьюдента; в) критерий Пирсона;

г) критерий ДарбинаEУотсона.

2.20.Какой коэффициент определяет среднее изменение результаB тивного признака при изменении факторного признака на 1 %:

а) коэффициент регрессии; б) коэффициент детерминации; в) коэффициент корреляции;

г) коэффициент эластичности.

2.21.Чему равен коэффициент эластичности, если уравнение

регрессии имеет вид y 2,02 0,78x , а средние значения признаков равны x 5, y 6 :

а) 0,94; б) 1,68; в) 0,65; г) 2,42.

25

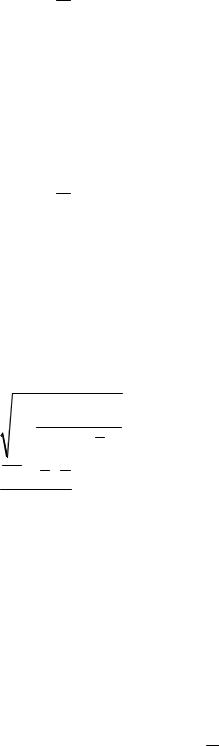
2.22. Уравнение степенной функции имеет вид: а) y a xb ;

б) y a bx ; в) y a bx ;

2.23. Уравнение гиперболы имеет вид: а) y a xb ;

б) y a bx ; в) y a bx ;

2.24. Индекс корреляции определяется по формуле:

б) 1 y y 2 ;

y y 2

в) xy x y ;

x y

2.25. Какое уравнение регрессии нельзя свести к линейному виду: а) y a xb ;

б) y a b ln x ; в) y a b xc .

2.26. Для функции y a bx средний коэффициент эластичности имеет вид:

26

2.27. Какое из следующих уравнений нелинейно по оцениваемым параметрам:

а) y a b ln x ;

в) y a bx ; г) y a bx .

2.28.Остаточная сумма квадратов равна нулю в том случае, когда

а) правильно подобрана регрессионная модель; б) между признаками существует точная функциональная связь;

в) между признаками существует тесная корреляционная связь.

2.29.Оценки параметров регрессии (свойства оценок метода наиB меньших квадратов) должны быть:

а) несмещенными; б) гетерокедастичными; в) эффективными; г) состоятельными.

2.30.Какой коэффициент расчета регрессии показывает долю учB тенной в модели вариации результативного признака y и обусловленной влиянием факторных переменных?

а) коэффициент регрессии; б) коэффициент детерминации; в) коэффициент корреляции;

г) коэффициент эластичности.

2.31.Укажите характеристики, используемые в качестве меры точности модели регрессии

а) средняя абсолютная ошибка; б) остаточная дисперсия; в) коэффициент корреляции;

г) средняя относительная ошибка аппроксимации.

2.32.Сопоставляя при регрессионном анализе факторную и остаB точную дисперсии, получим величину статистики:

а) Стьюдента; б) Дарбина; в) Пирсона; г) Фишера.

27

2.33.Уравнение регрессии признается в целом статистически знаB чимым, если

а) расчетное значение критерия Фишера больше соответствующего табличного значения;

б) расчетное значение критерия Фишера меньше соответствующего табличного значения;

в) расчетное значение критерия Фишера больше четырех; г) расчетное значение критерия Фишера больше нуля.

2.34.Построенное уравнение регрессии считается удовлетворительB ным, если значение средней ошибки аппроксимации не превышает

а) 5 %;

б) 10E12 %; в) 1 %; г) 95 %.

2.35.Как известно, индекс детерминации R2 используется для проB верки статистической значимости в целом уравнения нелинейной реB грессии по FBкритерия Фишера

где n – объем наблюдений. Поясните смысл параметра m. а) число параметров в уравнении регрессии;

б) число параметров при факторной переменной в уравнении реE грессии;

в) уровень значимости; г) среднее значение факторной переменной.

2.36. Требования, при которых модель считается адекватной, состоят в следующем:

1.Уровни i ряда остатков имеют случайный характер.

2.Математическое ожидание уровней ряда остатков равно нулю.

3.Дисперсия каждого отклонения i одинакова для всех значений x (свойство гомокедастичности).

4.Значения i независимы друг от друга, т.е. отсутствует автокорреляция.

5.Случайные величины i распределены по нормальному закону.

6.Число включаемых в регрессионную модель факторов в 6B7 раз меньше объема совокупности данных, по которым строится регрессия.

28

Укажите пункт, необязательный для адекватной модели регрессии.

а) 3; б) 4; в) 5; г) 6.

2.36.Наличие гетерокедастичности в остатках регрессии можно проверить с помощью теста

а) Пирсона;

б) ГольфельдаEКвандта; в) ДарбинаEУотсона;

г) Спирмена.

2.37.Зависимость последовательности остатков регрессии друг от друга в эконометрике называют

а) гомокедастичностью остатков; б) мультиколлинеарностью остатков; в) автокорреляцией остатков; г) гетерокедастичностью остатков.

2.38.Проверку независимости последовательности остатков (отB сутствие автокорреляции) осуществляют с помощью dBкритерия ДарB бинаBУотсона. Расчетное значение критерия определяется по формуле:

а) d i i 1 2 ;

2i

2.39. Оценить значимость парного линейного коэффициента корреB ляции можно при помощи

а) критерия Фишера;

б) теста ГольфельдаEКвандта;

в) критерия ДарбинаEУотсона; г) критерия Стьюдента.

29

2.40.Степень влияния неучтенных в модели факторов можно оценить с помощью:

а) коэффициента детерминации; б) коэффициента регрессии; в) средней ошибки аппроксимации;

г) построения линии регрессии.

2.41.По группе предприятий, производящих однородную продукцию, известна зависимость себестоимости единицы продукции y от нескольких факторов

Ранжировать факторы с помощью коэффициентов эластичности. Указать фактор снижения себестоимости.

а) объем производства; б) трудоемкость; в) цена на энергию;

г) отчисляемая доля прибыли.

2.42.Какая регрессия относится к основному виду регрессионных моделей в эконометрике?

а) линейная; б) нелинейная;

в) множественная; г) степенная.

2.43.Укажите аргументы в пользу использования линейных моделей

вэконометрике:

а) простота расчетов при параметризации;

30