Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

613

.pdf

Скачиваний:

Добавлен:

16.06.2024

Размер:

490.24 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 108 9 10 > Следующая >>>

Получили

x1 0,5x3 ,

x2 x3 ,

x3 любое.

x 0,5,	x 1,
1	1
x2 1,	x2 2,
x3 1.	x3 2.

Собственный вектор, соответствующий собственному значению1 9 , 9(1,2,2). Применим к нему процесс ортогонализации.

			1		1		2		2

h		9		1,2,2		,		,		.

	9		12 22 22		3 3 3

2,3	18 . Тогда
17 18			2		2		x			0			1			2	2 x			0
	2	14 18			4			1							2	4	4		1
	2	14 18			4		x2			0		,			2	4	4		x2		0	.
	2		4	14 18											2	4	4				0
	2		4	14 18			x3			0					2	4	4		x3		0
Применим метод Гаусса.
			x1	x2	x3
			1	2	2	0			1	2	2		0
			1	2	2	0			1	2	2		0
			2	4	4													0 .

						0	~		0	0	0		0	~ 1 2			2
			2	4	4	0			0	0	0		0
			2	4	4	0			0	0	0		0

Получили

x1 2x2 2x3 ,

x2, x3 любые.

У нас две свободные переменные ( x2 и x3 ). Применим метод бегуH

щей единицы (поочередно одну свободную переменную приравниваем единице, другую свободную переменную приравниваем нулю и нахоH дим соответствующее значение главной переменной).

x 2 1 2 0 2,		x 2 0 2 1 2,
	1	1	0,
x2 1,		x2
			1.
x3 0.		x3

f1( 2,1, 0) и	f2( 2, 0,1) – собственные векторы, соответствующие

собственному значению 2,3 18 . Применим к ним процесс ортогонаH лизации ГрамаHШмидта.


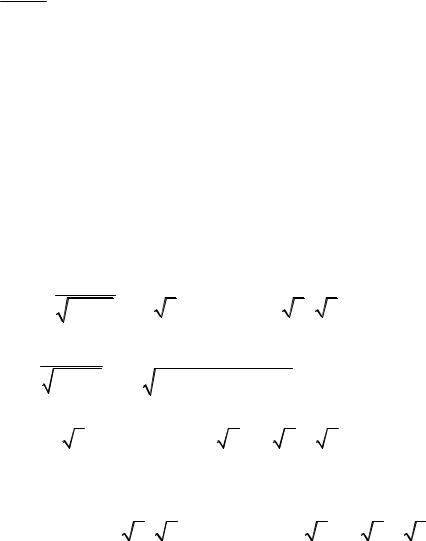
Сначала по f , f построим ортогональную систему g , g				2	.
1	2		1	2
	g	f	( 2,1, 0) .
	1	1

Тогда скалярные произведения:

g1 g2 ( 2)2 12 02 5 ,

																g				2 ( 2) 0 1 1 0 4 .
														f		g				2 ( 2) 0 1 1 0 4 .
														2				1
Найдем координаты вектора g2 .
				g																			4									1
			f	g										2,0,1									4		2,0,1							1		5 2,0,1 4													2,1,0
g2 f2			2			1			g1
g2 f2			2			1			g1														5									5
		g		g			2																5									5
			1				2
										1		10,0,5										8,4,0									1		2, 4,5									.
												10,0,5										8,4,0											2, 4,5									.
									5																					5
								на 5 (угол между векторами g																															и g						от этого не измеH
Умножим g						2		на 5 (угол между векторами g																															и g					2	от этого не измеH
						2																													1									2
нится) и полученный вектор вновь обозначим g2 : g2 ( 2, 4,5) .
Проверим, что g													g					:
									1							2
				g				g				2 ( 2) 1 ( 4) 0 5 4 4 0 0 .
						1			2
Построена ортогональная система g , g																																	. Получим из неё ортонорH
																													1			2
мированную систему h1,h2 .
												1							g1			1			2,1,0										2				1
				h1																		1													2			,	1			,0				.
				h1																			5												5			,				,0				.
												g1 g2											5												5					5
											1						g2											1								2, 4,5
			h2								1																	1
			h2
										g	2		g			2									2			(		2				5	2
											2					2						(		2)				(	4)					5
									1																			2						4				5
															2, 4,5															,							,						.
									3				5		2, 4,5												3		5	,		3					,			5			.
									3				5														3		5			3			5 3					5
Получили ортонормированный базис пространства
	1		2		2															2		1																2								4			5
h		,		,					,		h1										,				,0			и h2													,							,		.
h		,		,					,		h1									5	,		5		,0			и h2													,							,		.
	3 3 3																			5			5												3 5										3 5 3 5
В этом			базисе										квадратичная													форма								имеет							канонический вид
F 9y2	18y2 18y2 .
1		2							3

Матрица перехода от базиса e1(1,0,0), e2(0,1,0) , e3 (0,0,1) , в котором быH

ла задана исходная квадратичная форма F 17x 2	14x 2	14x 2	4x x	2
1	2	3	1	2

4x x	8x
4x x	8x		x		к базису h,h ,h		будет иметь вид (координаты векторов
1 3		2		3	1	2
h,h1,h2 нужно записать в столбцы матрицы):
							1		2		2

							3	5		3		5
							3	5		3		5
							2	1			4
					A								.
					A		3	5		3		5	.
							3	5		3		5
							2	0				5

							3			3		5
							3			3		5

	Заметим, что
										1					2								2							1							2	2

											3					5					3 5
																														3							3	3
																														3							3	3					1 0					0
			A AT							2 1													4							2							1
																																						0								0 1		0		E.
											3					5					3			5							5						5	0								0 1		0		E.
											3					5					3			5							5						5									0	0	1
																								5						2						4		5								0	0	1
										2						0								5						2						4		5


										3												3 5 3 5													3 5 3 5
	Такие преобразования называются ортогональными.
	Мы привели квадратичную форму ортогональным преобразованием
к каноническому виду.																																																		e (1,0,0),
	Координаты												вектора												x , x				2	, x		3		были				заданы							в		базисе			e (1,0,0),
e						e																					1		2			3																		1
e	(0,1,0) ,					e	(0,0,1) . Теперь y , y , y																										– это координаты вектора в базисе
2						3																					1		2			3
h,h1,h2 . Замена переменных происходит следующим образом:
																1							2					2											y1 2y2 2y3

																	3							5 3 5														3				5 3 5
	x							y									3							5 3 5									y					3				5 3 5
			1			A					1					2					1							4						1				2y				y					4y
		x								y																								y				1				2					3		,
		x	2							y																								y															,
			2								2						3							5 3 5										2				3				5 3 5
																	3							5 3 5														3				5 3 5
	x3							y3									2											5					y3							2y				5y
																					0																				1						3
																					0							3		5													3				5
																3												3		5											3		3				5
				x					y1			2y2								2y3					,
				x																					,
					1			3						5				3						5
								3						5				3						5
									2y							y						4y
то есть x						2					1					2								1		,
то есть x										3						5					3			5		,
										3						5					3			5
									2y1						5y3				.
				x		3			2y1						5y3
				x
										3				3			5

Задачи для самостоятельного решения

Написать матрицу квадратичной формы

96.F 2x12 5x22 8x32 4x1x2 2x1x3 6x2 x3 .

97.F x12 x22 x32 4x1x2 4x1x3 4x2 x3 .

98.F x12 2x22 3x32 2x1x2 2x2 x3

99.F 2x1x2 4x1x3 6x2 x3 .

Привести к каноническому виду квадратичную форму

100.F x12 3x22 4x32 2x1x2 2x1x3 6x2 x3 .

101.F 2x12 3x32 4x1x2 4x1x3 8x2 x3 .

102.F x12 2x1x2 2x2 x3 .

103.F x12 x32 4x2 x3 .

104.F x12 3x22 4x1x2 .

105.F x12 2x22 2x1x2 .

106.F 5x12 x1x2 .

107.F x22 6x1x2 .

108.F x12 x22 3x32 4x1x2 2x1x3 2x2 x3 .

109.F x1x2 x1x3 x2 x3 .

110.F x12 5x22 4x32 2x1x2 4x1x3 .

111.F 4x12 x22 x32 4x1x2 4x1x3 3x2 x3 .

112.F 3x12 2x22 x32 2x1x2 4x2 x3 .

113.F 2x12 3x22 4x32 2x1x2 4x1x3 3x2 x3 .

Найти все значения параметра , при котором положительно опреH делена квадратичная форма:

114.F 2x12 x22 x32 2x1x2 2x1x3 2x2 x3 .

115.F x12 2x22 3x32 2x1x2 2x1x3 4x2 x3 .

116.F 2 x12 x22 2x32 2x1x2 2x2 x3 .

117.F 2x12 x22 2x32 2x1x2 6x1x3 4x2 x3 .

Найти все значения параметра , при котором отрицательно опреH делена квадратичная форма:

118.F x12 x22 3x32 4x1x2 2x1x3 2x2 x3 .

119.F 2x12 2x22 x32 2x1x2 4x1x3 2x2 x3 .

120.F 2 x12 x22 x32 4x1x2 2x1x3 2x2 x3 .

121.F x12 2x22 2 x32 2x1x2 2x1x3 6x2 x3 .

Найти ортогональное преобразование неизвестных, приводящее квадратичную форму к каноническому виду, и записать полученный канонический вид:

122.F x12 4x22 x32 2x1x2 8x1x3 2x2 x3 .

123.F 3x12 x22 3x32 6x1x2 2x1x3 6x2 x3 .

124.F 6x12 3x22 2 x32 4x1x2 6x1x3 12x2 x3 .

125.F 5x12 5x22 5 x32 2x1x2 2x1x3 2x2 x3 .

126.F 17x12 17x22 11x32 16x1x2 8 x1x3 8 x2 x3 .

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

I. Вычислить определитель третьего порядка.

		2	3	1						3	0	1
		2	3	1						3	0	1
1.		0	1	2		.		16.		1	2	1			.
		0	3	4						3	2	0
	2		2	0						1	0	2
	2		2	0						1	0	2
2.		2	1		0			17.		3	1	0			.
	3		1	4						2	4	1
		5	0	2					1		0	2
		5	0	2					1		0	2
3.		3	1	2	.			18.	3		4	5				.
		1	0	1					0		6	1
		4	5	0						2	4	0
		4	5	0						2	4	0
4.		1	2	3		.		19.		1	1	3	.
		3	2	3						0	5	2
	1		1	2					3		1	2
	1		1	2					3		1	2
5.		2	0		3			20.	3		0			1		.
	5		0	1						2	3	0
		3	2	1						2	0	3
		3	2	1						2	0	3
6.		1	0	3		.		21.		1	5	2			.
		2	0	4						1	0	2
	4		0	2						1	3	0
	4		0	2						1	3	0
7.	5		1		0			22.		0	1	2		.
	3		2	1						2	4	0
8.	3		1	0				23.		1	2	0
	3		1	0						1	2	0
	2		5	4			.		0		1	2			.
	0		1	2					2		4	3
	1		4	3						1	1	2
	1		4	3						1	1	2
9.	0		2	5				24.		0	3	4			.
	1		2	0						2	3	0

10.		4	1		2					25.		3	1	0
		4	1		2							3	1	0
		2	1		4	.						2	1	2				.
		0	3		0							0	3	2
		0	1		3							1	2	1
		0	1		3							1	2	1
11.		2	0		1	.				26.		0	3				0	.
		1	2		0							2	2	1
		2	1		0							1	2	0
		2	1		0							1	2	0
12.		1 3			1	.				27.		3	1	4				.
		5	0		2							2	0	1
		0	2		1						3		0	1
		0	2		1						3		0	1
13.		3	2		4		.			28.	2		1	1		.
		1	0		5						3		0	2
		1	3		2							2	1	0
		1	3		2							2	1	0
14.		0	4		1	.				29.		1	2	2			.
		2	0		3							3	1	0
		3	1		2							2	2	3
		3	1		2							2	2	3
15.		4	0		5	.				30.		1	2	3				.
		0	1		3							0	1	0
II. Вычислить определитель четвертого порядка, разложив его по
элементам строки или столбца.
	1		1	2		0						3	1	2					0
	1		1	2		0						3	1	2					0
1.	3		6	2		5			.	16.		5	0		6				1		.
	1		0		6	4						2	2	1					3
	2		3		5		1					1	3	2					1
	2		0	1		3						1	1	0					3
	2		0	1		3						1	1	0					3
2.	6		3	9		0		.		17.		3	2	1					1			.
	0		2	1		3						1	2	1					3
	4		2		0	6						4	0	1					2
	2		7		2	1						5	0	4					2
	2		7		2	1						5	0	4					2
3.	1		1	1		0			.	18.		1	1	2					1	.
	3		4		0	2						4	1	2					0
	0		5	1			3					1	1	1					1

	4 5				1			5							6	2 10 4
	4 5				1			5							6	2 10 4
4.	3		2		8			2				.		19.	5	7	4	1								.
	5		3		1			3							2	4	2					6
	2		4 6 8												3	0 5 4
	3	2 0 5													1 2 4 1
	3	2 0 5													1 2 4 1
5.	4		3	5		3	0		.					20.	2	3	0	6						.
	1		0	2		3									2	2	1	4
	0	1 3 4													3	1 2		1
	3		5		3	2									1	2	3	4
	3		5		3	2									1	2	3	4
6.	2		4		1	0			.					21.	2	1	4	3							.
	1	2 2 1													3	4	1 2
	5	1 2 4													4	3 2				1
	2	1 2 0													1 1		2	3
	2	1 2 0													1 1		2	3
7.	3		4		1	2	.							22.	1	2	2	3			.
	2		1		0	1									2	3	1	0
	1		2		3	2									2	3	2	0
	3		2		0	2									1	2	0	4
	3		2		0	2									1	2	0	4
8.	1		1		2	3				.				23.	2	3	1	1	.
	4		5		1	0									3	1	2	4
	1		2		3	3									2	0	1	3
	0		4		1	1									4	1	2	0
	0		4		1	1									4	1	2	0
9.	4		2		1	3			.					24.	1	2	1 1					.
	0		1		2	2									3	1	2	1
	1		3		4	3									5	0	4	2
		0 2 1 7													4	3	2	1
		0 2 1 7													4	3	2	1
10.		4	8			2				3			.	25.	2	1	4	3					.
		10		1	5			4							0	4	1	2
		8 3				2 1									5	0	1 1
		5 3 7				1									3 5 1 2
		5 3 7				1									3 5 1 2
11.		3	2		0	2					.			26.	0	1	1	2					.
		2	1		4	6									3	1	3	0
		3	2		9	4									1	2	1	2

	4	1	1	5						2	2	0		3
	4	1	1	5						2	2	0		3
12.	0	2	2	3				.	27.	3	2	1		1		.
	3	4	1	2						1	1	2		1
	4	1	1	2						3	4	4		0
	1	8	2	3						6	0	1		1
	1	8	2	3						6	0	1		1
13.	3	2	0	4			.		28.	2	2	0		1	.
	5	3 7		1						1	1	3 3
	3	2	0	2						4	1	1		2
	2	3 4 1								1 2		3	4
	2	3 4 1								1 2		3	4
14.	4	2	3	2		.			29.	2	0	1		1		.
	3	0	2	1						3	3	1		0
	3	1	4	3						4	2	1		2
	3	1	2	3						4	1	2		0
	3	1	2	3						4	1	2		0
15.	4	1	2	4	.				30.	2	1	2		3		.
	1	1	1	1						3	0	1		1
	4	1	2	5						2	1	2		3

III. Найти произведение матриц А и В, если:

		1	2	1			0		1 2
1. а) A		3	0	4				4	5 0		;
1. а) A		3	0	4		, B		4	5 0		;
		1	5	0				1	1 4
		1	5	0				1	1 4
	1	3
							4
б) A	2	0			1		4		3
б) A	1	5		, B			0		.
	1	5			2		0		6

	6	3
		3	0	2			1		2 3
2. а) A		4	6	1				0		;
2. а) A		4	6	1		, B		0	4 1	;
		0	1	1				3
		0	1	1				3	0 5

1		2	3	1		2	4	1
1		2	3			1
б) A	0	1		, B	0	1	6	2
	0	1	1		1	1	0	2
					1	1	0	2

2		4	0	0		2	4
	3	1	1		1	3	3	;
3. а) A				, B
	1 3		5		2 0
							1

1		4	6				1
1		4	6					3
б) A		8		, B				3		.
2		8	0					0
								0
		1 4		2						0		1 1
4. а) A		3 6		0			, B				2	3 0				;
4. а) A		3 6		0			, B				2	3 0				;
		1 1		5							1
		1 1		5							1	4 1
1		4	1					2				4
1		4	1		, B
б) A		0			, B				0		1 .
2		0	3						5
									5			3
		2 0		2						1		1		0
5. а) A		1 4		3			, B				2	3 2					;
5. а) A		1 4		3			, B				2	3 2					;
		0	1	1							1	4		5
		0	1	1							1	4		5
2
	3
	3						0 2 .
б) A	1 , B 1						0 2 .
	0
	0

1
		1	2	0						4		0	1
6. а) A		3 4					, B				3					;
6. а) A		3 4		1			, B				3	2 1				;
		0	5	1							5	0	2
		0	5	1							5	0	2
1
	2
б) A	2	, B 2					0 3					0 .
	1

6
		3	4	0						1		1	4
7. а) A		2 2		1						2 0 3					;
7. а) A		2 2		1		, B				2 0 3					;
		1 0		5						3 1 2
		1 0		5						3 1 2

<<< < Предыдущая 1 2 3 4 5 6 78 / 108 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.06.2024487.35 Кб4609.pdf
#
16.06.2024169.42 Кб061.pdf
#
16.06.2024488.72 Кб0610.pdf
#
16.06.2024488.93 Кб0611.pdf
#
16.06.2024489.69 Кб2612.pdf
#
16.06.2024490.24 Кб0613.pdf
#
16.06.2024490.5 Кб0614.pdf
#
16.06.2024491.13 Кб0615.pdf
#
16.06.2024491.57 Кб0616.pdf
#
16.06.2024492.68 Кб0617.pdf
#
16.06.2024495.07 Кб0618.pdf

		2	3	1						3	0	1
		2	3	1						3	0	1
1.		0	1	2		.		16.		1	2	1			.
		0	3	4						3	2	0
	2		2	0						1	0	2
	2		2	0						1	0	2
2.		2	1		0			17.		3	1	0			.
	3		1	4						2	4	1
		5	0	2					1		0	2
		5	0	2					1		0	2
3.		3	1	2	.			18.	3		4	5				.
		1	0	1					0		6	1
		4	5	0						2	4	0
		4	5	0						2	4	0
4.		1	2	3		.		19.		1	1	3	.
		3	2	3						0	5	2
	1		1	2					3		1	2
	1		1	2					3		1	2
5.		2	0		3			20.	3		0			1		.
	5		0	1						2	3	0
		3	2	1						2	0	3
		3	2	1						2	0	3
6.		1	0	3		.		21.		1	5	2			.
		2	0	4						1	0	2
	4		0	2						1	3	0
	4		0	2						1	3	0
7.	5		1		0			22.		0	1	2		.
	3		2	1						2	4	0
8.	3		1	0				23.		1	2	0
	3		1	0						1	2	0
	2		5	4			.		0		1	2			.
	0		1	2					2		4	3
	1		4	3						1	1	2
	1		4	3						1	1	2
9.	0		2	5				24.		0	3	4			.
	1		2	0						2	3	0

		2	3	1						3	0	1
		2	3	1						3	0	1
1.		0	1	2		.		16.		1	2	1			.
		0	3	4						3	2	0
	2		2	0						1	0	2
	2		2	0						1	0	2
2.		2	1		0			17.		3	1	0			.
	3		1	4						2	4	1
		5	0	2					1		0	2
		5	0	2					1		0	2
3.		3	1	2	.			18.	3		4	5				.
		1	0	1					0		6	1
		4	5	0						2	4	0
		4	5	0						2	4	0
4.		1	2	3		.		19.		1	1	3	.
		3	2	3						0	5	2
	1		1	2					3		1	2
	1		1	2					3		1	2
5.		2	0		3			20.	3		0			1		.
	5		0	1						2	3	0
		3	2	1						2	0	3
		3	2	1						2	0	3
6.		1	0	3		.		21.		1	5	2			.
		2	0	4						1	0	2
	4		0	2						1	3	0
	4		0	2						1	3	0
7.	5		1		0			22.		0	1	2		.
	3		2	1						2	4	0
8.	3		1	0				23.		1	2	0
	3		1	0						1	2	0
	2		5	4			.		0		1	2			.
	0		1	2					2		4	3
	1		4	3						1	1	2
	1		4	3						1	1	2
9.	0		2	5				24.		0	3	4			.
	1		2	0						2	3	0

		2	3	1						3	0	1
		2	3	1						3	0	1
1.		0	1	2		.		16.		1	2	1			.
		0	3	4						3	2	0
	2		2	0						1	0	2
	2		2	0						1	0	2
2.		2	1		0			17.		3	1	0			.
	3		1	4						2	4	1
		5	0	2					1		0	2
		5	0	2					1		0	2
3.		3	1	2	.			18.	3		4	5				.
		1	0	1					0		6	1
		4	5	0						2	4	0
		4	5	0						2	4	0
4.		1	2	3		.		19.		1	1	3	.
		3	2	3						0	5	2
	1		1	2					3		1	2
	1		1	2					3		1	2
5.		2	0		3			20.	3		0			1		.
	5		0	1						2	3	0
		3	2	1						2	0	3
		3	2	1						2	0	3
6.		1	0	3		.		21.		1	5	2			.
		2	0	4						1	0	2
	4		0	2						1	3	0
	4		0	2						1	3	0
7.	5		1		0			22.		0	1	2		.
	3		2	1						2	4	0
8.	3		1	0				23.		1	2	0
	3		1	0						1	2	0
	2		5	4			.		0		1	2			.
	0		1	2					2		4	3
	1		4	3						1	1	2
	1		4	3						1	1	2
9.	0		2	5				24.		0	3	4			.
	1		2	0						2	3	0