1891

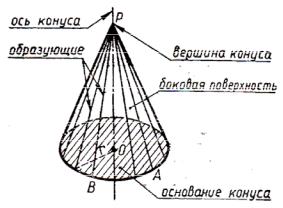
Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра. Осью цилиндра называется прямая, проходящая через центры оснований.

Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.

Рассмотрим сечения цилиндра различными плоскостями. Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называют осевым.

Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.

Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.

За площадь боковой поверхности цилиндра принимается площадь ее развертки, и она равна произведению длины окружности основания на высоту цилиндра.

Sбок 2 rh.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Так как площадь каждого

основания равна r2 , то для вычисления площади полной поверхности цилиндра получаем формулу

Sцил 2 r (r h) .

Объем цилиндра равен произведению площади основания на высоту.

VSосн h r2h .

2.2.Конус. Конусом (точнее круговым конусом) называется тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга, – вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания.

Отрезки, соединяющие вершину конуса с точками окружности основания,

называются образующими конуса.

Поверхность конуса состоит из основания и боковой поверхности.

Конус называется прямым, если прямая, соединяющая вершину конуса

сцентром основания, перпендику-

лярна плоскости основания.

121

Высотой конуса называется перпендикуляр, опущенный его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту.

Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым.

Если секущая плоскость перпендикулярна к оси конуса, то сечение конуса представляет собой круг с центром, расположенным на оси конуса.

Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

Sбок rl .

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Для вычисления площади полной поверхности конуса получается формула

Sкон r (l r) .

Объем конуса равен одной трети произведения площади основания на высоту.

V 13 Sосн h .

Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом.

Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.

Sбок (r r1)l .

122

Объем усеченного конуса, высота которого равна h, а площади оснований S и S1, вычисляется по формуле

2.3. Сфера. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. Данная точка называется центром сферы, а данное расстояние –

радиусом сферы.

Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через ее центр,

называется диаметром сферы.

Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.

Если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность.

Если секущая плоскость проходит через центр шара, то в сечении получается круг, радиус которого равен радиусу шара. Такой круг называется большим кругом шара.

Плоскость, имеющая со сферой только одну общую точку, называется

касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.

Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Площадь сферы вычисляется по формуле

S 4 R2 .

Объем шара равен 43 R3 .

123

§3. Примеры решения задач

Пример 1 . Основанием прямой призмы является параллелограмм, стороны которого равны 3 и 8, а угол между ними 60 . Найдите площадь боковой поверхности призмы, если известно, что площадь ее меньшего

диагонального сечения равна 70.

Решение. 1) Пусть ABCDA1B1C1D1 –

прямая призма и ее основание параллелограмм ABCD, в котором АВ=СD=8,

ВС=АD=3, BAD 60 . Отсюда ВD –

меньшая диагональ основания и, значит, ВDD1В1 – меньшее диагональное сечение,

аего площадь S BD BB1 70.

2)По теореме косинусов в треугольнике АВD имеем

BD2 AB2 AD2 2 AB AD cos( BAD) 64 9 2 8 3 cos60 49 .

Значит, ВD=7 и ВВ1=10.

3) Площадь боковой поверхности призмы находим по формуле

Sбок 2(AB BC) BB1 .

Получим Sбок 2(8 3) 10 220 .

Ответ: 220.

Пример 2. Концы отрезка АВ лежат на окружностях оснований ци-

линдра. Высота цилиндра равна 12 3 , радиус основания равен 10, а угол между прямой АВ и плоскостью основания цилиндра равен 60 . Найдите расстояние между осью цилиндра и параллельной ей плоскостью, проходящей через точки А и В.

Решение. 1) Пусть А1 и В1 – проекции точек А и В на соответственно противоположные им основания, точки О и О1 – центры оснований. Тогда

AA1 BB1 OO1 , AA1 BB1 .

Поэтому АА1ВВ1 – прямоугольник, угол ВАВ1 – угол между прямой АВ и плоскостью основания цилиндра, а плоскость ABB1 OO1 . По условию

2) Пусть ОD – высота треугольника АОВ1. Так как плоскость основания цилиндра перпендикулярна плоскости АВВ1, то OD ABB1 и, значит,

124

длина ОD равна искомому расстоянию между осью цилиндра и плоскостью АВВ1.

3) Треугольник АОВ1 – равнобедренный. Поэтому OD – медиана

Ответ: 9.

Пример 4. В пирамиде КАВС ребро КВ перпендикулярно плоскости

основания. Угол между плоскостями АСК и АВС равен 45 , ACB 90 , АВ=13, АС=12. Найдите высоту пирамиды.

125

Решение. 1) KB ABC , КС – наклонная, ВС – проекция КС. Так как BC AC , то KC AC (теорем о трех перпендикулярах).

2) BC AC и KC AC , следовательно,

BCK – линейный угол двугранного угла при ребре АС, поэтому BCK 45 .

3)В треугольнике АВС: BC2 AB2 AC2 (по теореме Пифагора), ВС=5.

4)KB ABC , следовательно, КВ – высота

пирамиды и KB BC . Так как BCK 45 , то

КВ=ВС=5. Ответ: 5.

Пример 5. Дан куб ABCDA1B1C1D1. Через точки С, D1 и середину ребра АА1 проведена секущая плоскость. Найдите площадь сечения, если ребро куба равно 4.

Решение. 1) Прямые CD1 и ML лежат как в плоскости сечения, так и в параллельных плоскостях противоположных граней куба, поэтому CD1 ML . Так как

CD1 ML , то сечение MLCD1 – трапе-

ция.

Треугольники MA1D1 и MAT равны

по катету и острому углу. Отсюда следует, что AT A1D1 AD 4 .

Для нахождения высоты трапеции, вычислим длину СН.

126

Из прямоугольного треугольника CHL имеем

LH 2 CL2 CH 2 20 2 18 , LH 3 2 .

Тогда площадь равна:

Ответ: 18.

Пример 6. Диаметр основания конуса равен 6 м, образующая наклонена к плоскости основания под углом 60 . Найдите площадь описанной около конуса сферы.

Решение. 1) Пусть С – вершина конуса, О – центр основания, АСВ – осевое сечение конуса. Поскольку образующая конуса наклонена к плоскости основания под углом 60 и СО – высота конуса, то прямая АВ – проекция прямой СА на плоскость основания конуса. Следовательно, CAB равен углу между образующей конуса и площадью

его основания. Поэтому CAB 60 и равнобедренный треугольник АВС – правильный. Отсюда следует, что CA AB BC 6 м.

2)Найдем положение центра сферы, описанной около конуса. По определению такой сферы, окружность основания конуса – сечение описанной сферы и вершина конуса лежит на этой сфере. По свойству диаметра сферы, проходящего через центр любого ее сечения, прямая СО

перпендикулярна плоскости основания конуса и поэтому центр О1 описанной сферы лежит на прямой СО. Отсюда следует, что центр О1 сферы, описанной около конуса, есть центр окружности, описанной около его осевого сечения.

3)В правильном треугольнике АВС

R O1C AB3 3 6 33 2 3 ( м) .

4) Найдем площадь сферы: S 4 R2 4 2 3 2 48 (м2).

Ответ: 48 .

127

Пример 7. Основание пирамиды – равнобедренный треугольник,

Осталось найти высоту DO пирамиды.

3) Так как DA DB DC , то проекции этих ребер на плоскость основания АВС пирамиды равны. То есть OA OB OC . Следовательно, точка О находится на одинаковых расстояниях от вершины треугольника АВС, т.е. является центром окружности, описанной около основания пирамиды.

Рассмотрим треугольник АВС. Требуется найти радиус описанной около треугольника окружности. Найдем его с помощью теоремы синусов.

Ответ: 3.

Пример 8. Сторона основания правильной призмы ABCDA1B1C1D1

равна 12, а боковое ребро 2 6 . Найдите градусную меру угла между плоскостями АВ1С и АВС.

128

Решение. 1) Плоскость АВ1С пересекает плоскость АВС по прямой АС. Построим линейный угол двугранного угла ВАСВ1 .Для этого из точки В проведем перпендикуляр к прямой АС. Так как

призма ABCDA1B1C1D1 правильная, то ее основанием является правильный четырехугольник – квадрат. Диагонали квадрата взаимно перпендикулярны, следовательно, искомый перпендикуляр – отрезок ВО – половина диагонали ВD, причем точка О – середина отрезка АС. Поскольку призма правильная, то она прямая, значит, боковые ребра перпендикулярны плоскости основания.

Следовательно, прямая ВО является проекцией наклонной В1О. По теореме о трех перпендикулярах наклонная В1О

перпендикулярна прямой АС. Тогда угол ВОВ1 является линейным углом двугранного угла ВАСВ1 .

дует, что прямая ВВ1 перпендикулярна любой прямой, лежащей в плоскости АВС. Поэтому треугольник ОВВ1 прямоугольны, и значит,

tg 62 62 33 . Следовательно, BOB1 30 .

Ответ: 30 .

Пример 9. В основании прямой призмы АВСА1В1С1 лежит равнобедренный прямоугольный треугольник АВС ( B 900 ) . Объем призмы

равен 54 6 . Плоскость АВ1С наклонена к плоскости основания под углом

60 . Найдите катет АВ.

Решение. 1) Линейный угол между плоскостями АВС и АВ1С есть HBB1 , где ВН – высота

треугольника АВС. По теореме о трех перпендикулярах наклонная В1Н – также перпендикулярна прямой АС, т.е. отрезок В1Н – высота треугольника АВ1С.

2) По условию задачи треугольник АВС равнобедренный и прямоугольный.

Пусть AB x , тогда BH 12 AC x 22 .

129

Ответ: 6.

Пример 10. В основании пирамиды SABCD лежит квадрат ABCD со

стороной 2 3 . Боковое ребро DS перпендикулярно плоскости основания, а граньABS наклонена к плоскости основания под углом 30 . Найдите объем пирамиды.

Решение. 1) Плоскости ABS и АВС пересекаются

по прямой АВ. Основание ABCD пирамиды –

квадрат, следовательно, AD AB . По теореме о

трех перпендикулярах AS AB , (прямая AD –

проекция прямой AS на плоскость основания), т.е.

угол SAD – линейный угол двугранного угла SABD,

расстояние от вершины С до плоскости BDC1. Решение. 1) Если провести перпендикуляр СХ к

плоскости BDC1, то его длина будет искомым расстоянием от точки С до этой плоскости. Для построения СХ проведем через точку С плоскость, перпендикулярную плоскости BDC1, а затем в этой плоскости построим прямую, перпендикулярную линии пересечения плоскостей.

130