
1879
.pdf
|
|
Таблица 3.1 |
|
№ |
Материал основания |
|
k, МПа/м |
п/п |
|
|
|
1 |
Песок свеженасыпанный |
|
1 5 |
|
Глина мокрая, размягченная |
|
|
|
|
|
|
2 |
Грунты средней плотности: |
|
|
|
песок слежавшийся; |
|
5 50 |
|
гравий насыпной; |
|
|
|
|
|
|
|
глина влажная |
|
|
3 |
Грунты плотные: |
|
|
|
песок и гравий, плотно слежавшийся; |
|
50 100 |
|
щебень; |
|
|
|
|
|
|
|
глина малой влажности |
|
|
4 |
Грунты весьма плотные: |
|
|
|
грунт песчано-глинистый, искусственно уплотненный; |
|
100 200 |
|
глина твердая; |
|
|
5 |
Известняк, песчаник, мерзлота |
|
200 1000 |
6 |
Твердая скала |
|
1000 15000 |
Реакцию нелинейно-упругого основания можно смоделировать следующими соотношениями:
а) для основания с жесткой упругой характеристикой в виде
|
r k wh , |
|
|
(3.46) |
|
где h>1; |
|
|
|
|
|
б) для основания с мягкой упругой характеристикой |
|
||||
r k w k3 |
w3 . |
(3.47) |
|||
Коэффициент k3 определяется из соотношения |
|
||||
k3 |
|
k wпп rпп |
, |
(3.48) |
|
3 |
|
||||
|
|
w |
|
|
|
|
|
пп |
|
|
|
где rпп – максимальная возможная реакция в точке основания; wпп – соответствующее перемещение.
Коэффициент k3 может быть вычислен из соотношения:
k |
|
|
4 k3 |
. |
(3.49) |
|||
3 |
|
|
|
|||||
27 r2 |
||||||||
|
|
|
|
|||||
|
|
|
|
|
пп |
|
|
|
Последнее вытекает из экстремума функции r.
Таким образом, система динамического равновесия «сооружение – гаситель» расширится на три уравнения с тремя неизвестными функциями х,у иw0. Приэтомперемещенияопорныхузловыхточексооружения(башни) в вертикальном направлении ир из числа фиксированных перемещений перейдут в состав переменных, связанных с плитой соотношениями вида
61
(3.44). Здесь индекс p равен номерам вертикальных перемещений. Строки матрицы жесткости системы «сооружение – гаситель» дополнятся элементами
ki, n 2 ki, p ;
k |
|
ki, p yl ; |
(3.50) |
|
i, n 1 |
|
ki, n ki, p xl .
Здесь i – номер строки (i =1, 2, …, n–2); l – номер опорного узла, соответствующего перемещению p; n – количество неизвестных перемещений системы «основание – сооружение – гаситель».
При определении собственных частот системы ОСГ (основание – сооружение – гаситель) необходимо иметь в виду, что в правых частях уравнений (3.45) стоят, вообще говоря, внутренние силы. Поэтому эти уравнения целесообразно переписать, переместив правые части влево, одновременно выразив внутренние силы через узловые перемещения.
Врядеслучаевфундаментыопорныхузловвысотныхсооружениймогут быть выполнены независимыми друг от друга. В этих случаях упругую реакцию основания каждого фундамента легко определить с помощью соотношения
ri ki Ai , |
(3.51) |
где Аi – площадь основания i-го фундамента. Такая форма записи позволяет моделировать местные ослабления или, наоборот, местные жесткие включения грунтовых оснований.
62
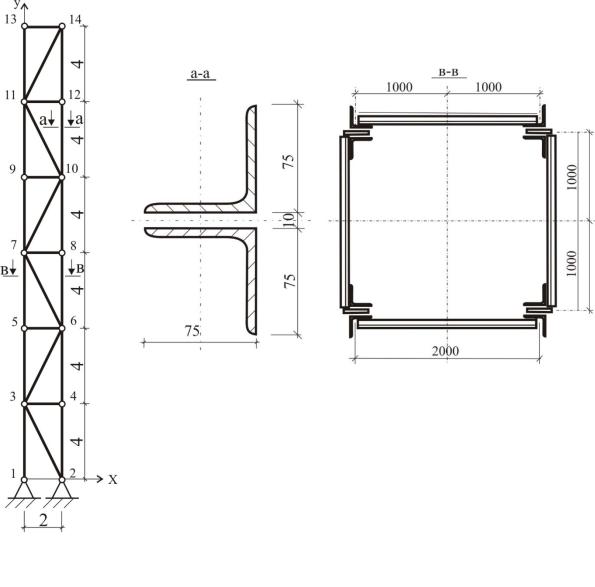
4. РАСЧЕТ БАШНИ НА СЕЙСМИЧЕСКИЕ ВОЗДЕЙСТВИЯ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ В MATHCAD
Содержание курсовой работы
Задание на расчетную работу............................................................................
Формирование математической модели башни в MathCad………………... Поиск вектора собственных значений, вектора частот и собственного вектора Расчетколебанийбашниподанному в заданиизаконудвижения……………
Расчетпозаконудвиженияреальногоземлетрясения(поакселерограмме)…
4.1. Задание на расчетную работу
Дано: Все элементы из уголков 75 75 7
Колебания основания происходит по закону
0,5sin(4t) 0,3sin(10t)см
Цель: произвести сейсмический расчет башни (плоской фермы).
1.Определить максимальные горизонтальные перемещения узлов башни методом центральных разностей.
2.Определить силы инерции
in mi (Ui )
3.Определить усиление в стержнях
i i( р ф)
4.Определить напряжение в стержнях.
63
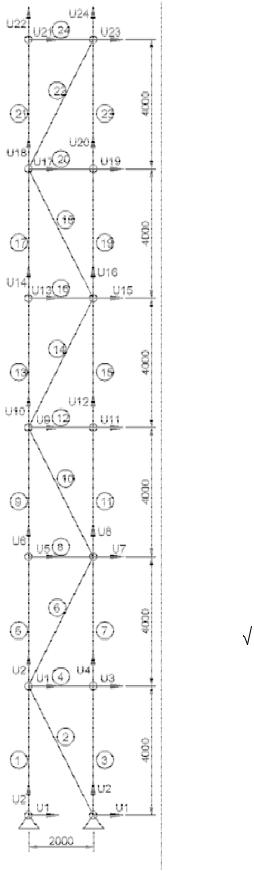
4.2.Формирование математической модели башни в MathCad
Башня высотой H=24 м, все элементы которой выполнены из равнополочных уголков 75 75 7 мм (в сечении размещены два уголка).
Модуль упругости E = 210 000 МПа, площадь одного уголка А = 10.15 см2, погонный вес уголков g = 7.96 кг/м.п.
Для работы в программном комплексе MathCad стоит учесть, что в подсчетах удобнее задаваться одной единицей измерения. В данном случае за единицу длины мы примем 1 м, а площади – 1 м2 соответственно.
Задаем начальные данные в MathCad:
ES 2.1 1011 |
AS 20310 5 |
PM 7.96 |
Составим локальные матрицы жесткости для типовых элементов – стоек и раскосов нашей башни. Для этого мы должны определить синусы и косинусы углов α наших элементов. Угол α соответствующего элемента отмеряем против часовой стрелки от горизонтали, проведенной из начального узла элемента до него самого.
l1 4 |
s1 1 |
c1 0 |
|
|
|
|
||||
|
|
|
|
|
c1 c1 |
c1 s1 |
(c1 c1) |
(c1 s1) |
||
k1 |
(ES AS) |
c1 s1 |
s1 s1 |
(c1 s1) |
(s1 s1) |
|||||
|
l1 |
|
|
|
(c1 s1) |
c1 c1 |
c1 s1 |
|
||
|
|
|
(c1 c1) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(c1 s1) |
(s1 s1) |
c1 s1 |
s1 s1 |
|
||
l2 |
|
|
c2 |
0.45399 |
s2 |
|
0.891 |
|||
20 |
|
|||||||||
|
|
|
|
|
c2 c2 |
c2 s2 |
(c2 c2) |
(c2 s2) |
||
k2 |
(ES AS) |
c2 s2 |
s2 s2 |
(c2 s2) |
(s2 s2) |
|||||
|
l2 |
|
|
|
(c2 s2) |
c2 c2 |
c2 s2 |
|
||
|
|
|
(c2 c2) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(c2 s2) |
(s2 s2) |
c2 s2 |
s2 s2 |
|
||
64

|
|
l3 2 |
c3 |
1 |
|
s3 |
|
0 |
|
|
|||||
|
|
|
|
|
|
|
c3 c3 |
|
c3 s3 |
|
(c3 c3) |
(c3 s3) |
|||
k3 |
|
(ES AS) |
c3 s3 |
|
s3 s3 |
|
(c3 s3) |
(s3 s3) |
|||||||
|
l3 |
|
|
|
|
(c3 s3) |
c3 c3 |
|
c3 s3 |
|
|||||
|
|
|
(c3 c3) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(c3 s3) |
(s3 s3) |
c3 s3 |
|
s3 s3 |
|
||||
|
|
l4 |
4 |
c4 |
0 |
|
s4 1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
c4 c4 |
|
c4 s4 |
|
(c4 c4) |
(c4 s4) |
|||
k4 |
|
(ES AS) |
c4 s4 |
|
s4 s4 |
|
(c4 s4) |
(s4 s4) |
|||||||
|
l4 |
|
|
|
|
(c4 s4) |
c4 c4 |
|
c4 s4 |
|
|||||
|
|
|
(c4 c4) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(c4 s4) |
(s4 s4) |
c4 s4 |
|
s4 s4 |
|
||||
l5 |
|
|
|
|
c5 |
0.45399 |
|
s5 0.89 |
|
|
|||||
20 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
c5 c5 |
|
c5 s5 |
(c5 c5) |
(c5 s5) |
|
||||
k5 |
(ES AS) |
|
|
c5 s5 |
|
s5 s5 |
(c5 s5) |
(s5 s5) |
|
||||||
|
l5 |
|
|
(c5 s5) |
|
c5 c5 |
|
c5 s5 |
|
|
|||||
|
|
|
(c5 c5) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
(c5 s5) |
(s5 s5) |
|
c5 s5 |
|
s5 s5 |
|
|
|||
l6 |
20 |
c6 0.45399 |
s6 |
0.891 |
|
||||
|
|
|
|
|
c6 c6 |
c6 s6 |
(c6 c6) |
(c6 s6) |
|
|
|
|
|
|
c6 s6 |
s6 s6 |
(c6 s6) |
|
|
k6 |
(ES AS) |
(s6 s6) |
|||||||
|
l6 |
|
|
|
(c6 s6) |
c6 c6 |
c6 s6 |
|
|
|
|
|
(c6 c6) |
|
|||||
|
|
|
|
|
|
(s6 s6) |
c6 s6 |
s6 s6 |
|
|
|
|
|
(c6 s6) |
|
||||
В нашем случае имеем 6 типов матриц жесткости, которые характеризуют все наши 24 стержня башни.
Введем в MathCad матрицы Еi размерностью 4 28, необходимые нам для перевода локальных матриц жесткости стержней в глобальные. В этих матрицах все элементы, за исключением четырех, будут нулевыми. Четыре единичных элемента в них будут соответствовать номерам перемещений, которые может совершать соответствующий i-й стержень.
65
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
E1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
|
|
||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
|
|||
|
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
|
|
|||||||||||||||||||||||||||||||||
E2 |
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
|
|
|||||||||||||||||||||||||||||||||
|
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
0 1 0 |
|
|
||||||||||||||||||||||||||||||||
|
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 |
|
|
|||||||||||||||||||||||||||||||||
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
E3 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
|
|
||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
|
|||
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
E4 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|
||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
E5 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|
||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
E6 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|
||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
E7 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|
||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
E8 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|
||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
E9 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|
||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|||
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
||
E10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
||
66
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
E11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
E12 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
E13 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
E14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
E15 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
E16 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
E17 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|||
E18 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
E19 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
E20 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|||
67
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
E21 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||
|
|||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
E22 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
||
|
|||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
E23 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
||
|
|||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
E24 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
||
|
|||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|||
Составим отдельные глобальные матрицы i-го элемента, а затем просуммируем их, получив глобальную матрицу жесткости всей нашей системы.
KK1 E1T k1 E1 |
KK11 E11T k4 E11 |
KK21 E21T k4 E21 |
|||
KK |
E2T k2 E2 |
KK |
E12T k3 E12 |
KK22 E22T k5 E22 |
|
2 |
|
12 |
|
|
|
KK3 E3T k1 E3 |
KK13 E13T k4 E13 |
KK23 E23T k4 E23 |
|||
KK4 E4T k3 E4 |
KK14 E14T k5 E14 |
T |
|||
KK |
E5T k4 E5 |
KK |
E15T k4 E15 |
KK24 E24 k3 E24 |
|
5 |
|
15 |
|
24 |
|
KK6 E6T k5 E6 |
KK16 E16T k3 E16 |
||||
KK KKI |
|||||
|
T |
|
T |
I 1 |
|
KK7 E7 k4 E7 |
KK17 E17 k4 E17 |
|
|||
KK |
E8T k3 E8 |
KK |
E18T k6 E18 |
|
|
8 |
|
18 |
|
|
|
KK |
E9T k5 E9 |
KK |
E19T k4 E19 |
|
|
9 |
|
19 |
|
|
|
KK |
E10T k6 E10 |
KK |
E20T k3 E20 |
|
|
10 |
|
20 |
|
|
|
68
Далее зададимся типовыми массами перемещений узлов башни. Стоит помнить, что сечение каждого стержня составляют два равнополочных уголка. Также при подсчете масс перемещений узлов башни нужно представлять заданную башню как объемную конструкцию; исходя из этого, в нашем варианте получим две типовые массы.
M1 |
2 PM |
20 |
|
20 |
|
2 |
|
2 |
|
4 |
|
4 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
(соответствует перемещениям узлов с 1-го |
|||||||||
2 |
|
2 |
|
2 |
|
2 |
|
2 |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
по 20 включительно) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
M21 2 PM |
|
|
20 |
|
2 |
|
2 |
|
4 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
(соответствует перемещениям узлов под |
|||||||||||
|
|
|
2 |
|
2 |
2 |
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
номерами 21, 22, 23 и 24)
Матрица масс будет представлять собой диагональную нулевую матрицу.
M1
00
0
0000
0
000
M 0
0
00000
0
000
0
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M21 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M21 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
M21 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
M21
71
4.3.Поиск вектора собственных значений, вектора частот
исобственного вектора
Применив функцию eigenvals (AA) к матрице вида AA:=M–1 KO, получаем вектор собственных значений.
Частоты λ колебаний башни находятся как корень квадратный из собственного значения и реализуется в пакете MathCad в радианах и герцах, соответственно.
Сортируем частоты по возрастанию с помощью функции sort.
eigenvals(AA) |
|
|
|
|
|
|
|
|
gc |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
||||||||||||
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|||
|
1 |
4.488·106 |
|
1 |
|
2.118·103 |
|
|
1 |
337.168 |
|
1 |
732.238 |
||||
|
2 |
3.587·106 |
|
2 |
|
1.894·103 |
|
|
2 |
301.411 |
|
2 |
7.005·103 |
||||
|
3 |
3.162·106 |
|
3 |
|
1.778·103 |
|
|
3 |
283.027 |
|
3 |
3.192·104 |
||||
|
4 |
3.021·106 |
|
4 |
|
1.738·103 |
|
|
4 |
276.61 |
|
4 |
5.432·104 |
||||
|
5 |
2.833·106 |
|
5 |
|
1.683·103 |
|
|
5 |
267.876 |
|
5 |
9.34·104 |
||||
|
6 |
2.815·106 |
|
6 |
|
1.678·103 |
|
|
6 |
267.014 |
|
6 |
1.229·105 |
||||
|
7 |
2.648·106 |
|
7 |
|
1.627·103 |
|
|
7 |
258.987 |
|
7 |
2.393·105 |
||||
|
8 |
2.623·106 |
|
8 |
|
1.62·103 |
|
|
8 |
257.762 |
|
8 |
5.069·105 |
||||
|
9 |
2.435·106 |
|
9 |
|
1.56·103 |
|
|
9 |
248.34 |
|
9 |
6.432·105 |
||||
|
10 |
2.241·106 |
|
10 |
|
1.497·103 |
|
|
10 |
238.233 |
|
10 |
8.327·105 |
||||
|
11 |
2.089·106 |
|
11 |
|
1.445·103 |
|
|
11 |
230.03 |
|
11 |
1.021·106 |
||||
|
12 |
1.891·106 |
|
12 |
|
1.375·103 |
gc |
|
12 |
218.859 |
sort |
12 |
1.167·106 |
||||
|
13 |
1.167·106 |
|
13 |
|
1.08·103 |
|
|
13 |
171.914 |
|
13 |
1.891·106 |
||||
|
14 |
1.021·106 |
|
14 |
|
1.01·103 |
|
|
14 |
160.797 |
|
14 |
2.089·106 |
||||
|
15 |
8.327·105 |
|
15 |
|
912.525 |
|
|
15 |
145.233 |
|
15 |
2.241·106 |
||||
|
16 |
6.432·105 |
|
16 |
|
801.993 |
|
|
16 |
127.641 |
|
16 |
2.435·106 |
||||
|
17 |
5.069·105 |
|
17 |
|
711.965 |
|
|
17 |
113.313 |
|
17 |
2.623·106 |
||||
|
18 |
2.393·105 |
|
18 |
|
489.183 |
|
|
18 |
77.856 |
|
18 |
2.648·106 |
||||
|
19 |
732.238 |
|
19 |
|
27.06 |
|
|
19 |
4.307 |
|
19 |
2.815·106 |
||||
|
20 |
7.005·103 |
|
20 |
|
83.696 |
|
|
20 |
13.321 |
|
20 |
2.833·106 |
||||
|
21 |
3.192·104 |
|
21 |
|
178.669 |
|
|
21 |
28.436 |
|
21 |
3.021·106 |
||||
|
22 |
5.432·104 |
|
22 |
|
233.069 |
|
|
22 |
37.094 |
|
22 |
3.162·106 |
||||
|
23 |
9.34·104 |
|
23 |
|
305.618 |
|
|
23 |
48.641 |
|
23 |
3.587·106 |
||||
|
24 |
1.229·105 |
|
24 |
|
350.626 |
|
|
24 |
55.804 |
|
24 |
4.488·106 |
||||
Выбираем наименьшую из частот собственных колебаний – это и будет частота, соответствующая первой форме свободных колебаний. Выбираем, по возрастающей, четыре частоты собственных колебаний и, используя соответствующие столбцы матрицы собственных векторов АА, строим первые четыре формы собственных колебаний (для левой стойки).
72
