
1775
.pdf
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования «Пензенский государственный университет архитектуры и строительства»
(ПГУАС)
Н.А. Очкина
ФИЗИКА
ОСНОВЫ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
Рекомендовано Редсоветом университета в качестве учебного пособия для студентов,
обучающихся по направлению 08.03.01 «Строительство»
Под общей ред. доктора технических наук, профессора Г.И. Грейсуха
Пенза 2016 1
УДК 537
ББК 22.313 О-95
Рецензенты:
кандидат технических наук, доцент С.В. Тертычная (ПГУ); кандидат физико-математических
наук, доцент П.П. Мельниченко (ПГУАС)
Очкина Н.А.
Физика. Основы классической электродинамики: учеб. пособие О-95 по направлению подготовки 08.03.01 «Строительство»/ Н.А. Очкина; под общ. ред. д-ра техн. наук, проф. Г.И. Грейсуха. – Пенза:
ПГУАС, 2016. – 184 с.
Кратко изложен материал по шести разделам электродинамики вузовского курса общей физики. Рассмотрены основные вопросы электростатики, законы цепей постоянного электрического тока, элементы теории магнитного поля, индукционные явления, основы электромагнитной теории Максвелла. Приведены вопросы для самоконтроля и повторения.
Подготовлено на кафедре «Физика и химия» и предназначено для использования студентами, обучающимися по направлению подготовки 08.03.01 «Строительство», при изучении дисциплины «Физика».
©Пензенский государственный университет архитектуры и строительства, 2016
©Очкина Н.А., 2016
2
ПРЕДИСЛОВИЕ
Настоящее учебное пособие написано в соответствии с программой курса «Физика» ФГОС ВО третьего поколения для направления подготовки 08.03.01 «Строительство» и имеет целью совершенствование следующих компетенций:
способность использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического и компьютерного моделирования, теоретического и экспериментального исследования;
способность выявить естественнонаучную сущность проблем, возникающих в ходе профессиональной деятельности, привлечь их для решения соответствующий физико-математический аппарат;
способность владеть эффективными правилами, методами и средствами сбора, обмена, хранения и обработки информации, навыками работы с компьютером как средством управления информацией.
Пособие содержит шесть глав, в которых последовательно излагаются основные вопросы, предусмотренные государственными образовательными стандартами для изучения раздела «Основы классической электродинамики» по дисциплине «Физика» в высших учебных заведениях.
В каждой главе дается подробное изложение основ теории по электрическим и магнитным явлениям и приводятся вопросы для самоконтроля, которые помогут студентам самостоятельно оценить качество усвоения теоретического материала.
Систематическая работа с пособием, в учебной аудитории, и во внеаудиторное время способствует формированию у студентов:
знаний сущности основных физических явлений и физических законов в области электричества и магнетизма;
умений использовать основные законы электромагнетизма в профессиональной деятельности; применять методы компьютерного моделирования для теоретического и экспериментального исследований;
вырабатывает способность владеть эффективными правилами, методами и средствами сбора, обмена, хранения и обработки информации, навыками работы с компьютером как средством управления информацией; приемами правильной эксплуатации основных приборов и оборудования; методами обработки и интерпретирования результатов эксперимента.
В тексте учебного пособия наиболее важные положения и термины, а также формулировки законов выделены курсивом. Это способствует более эффективному усвоению материала студентами.
3
ВВЕДЕНИЕ
Электродинамика – это наука о свойствах и закономерностях поведения особого вида материи – электромагнитного поля, осуществляющего взаимодействие между электрически заряженными телами или частицами.
Электромагнитное взаимодействие является одним из четырёх фундаментальных взаимодействий. Оно не универсальное и в зависимости от знака заряда может выступать как притяжение, либо как отталкивание. Электромагнитное взаимодействие относительно сильное и проявляется на любых расстояниях, поэтому с ним связано большое явлений. Оно определяет возникновение атомов, молекул и макроскопических тел; электромагнитные распады ядер и частиц; процессы ионизации и возбуждения атомов среды. Примерами проявления электромагнитного взаимодействия на макроскопическом уровне являются силы упругости в твёрдых телах, силы вязкости и поверхностного натяжения в жидкостях.
К созданию электродинамики привела длинная цепь планомерных исследований и случайных открытий, начиная с обнаружения способности янтаря, потертого о шерсть, притягивать легкие предметы и заканчивая гипотезой Д. Максвелла о порождении магнитного поля переменным электрическим полем. Лишь во второй половине XIX в., после создания электродинамики, началось широкое практическое использование электромагнитных явлений. Изобретение радио А.С.Поповым (1859-1906) и Г. Маркони (1874-1937) – одно из важнейших применений принципов новой теории. Электромагнитные взаимодействия широко используются в радиотехнике, электронике, электротехнике.
Как отдельная часть физики электродинамика состоит из следующих разделов: учение о поле неподвижных электрически заряженных тел и частиц, учение об электрическом токе, учение о магнитном поле и электромагнитной индукции, учение об электромагнитных колебаниях и волнах.
Все эти разделы в единое целое объединяет учение Д. Максвелла, который не только разработал стройную теорию электромагнитного поля, но и доказал его реальное существование. Теория Д. Максвелла доказала, что известные в науке электрическое и магнитное поля являются проявлением единого электромагнитного поля в различных системах отсчета.
4
1.ЭЛЕКТРОСТАТИКА
1.1.Закон сохранения заряда. Взаимодействие зарядов.
Закон Кулона
Известно, что одноименные заряды отталкиваются, разноименные – притягиваются. Если поднести заряженное тело (с любым зарядом) к легкому – незаряженному, то между ними будет притяжение (явление электризации легкого тела через влияние). На ближайшем к заряженному телу конце появляются заряды противоположного знака (индуцированные заряды). Это явление называется электростатической индукцией.
Опыт показывает, что возникновение заряда на любом теле сопровождается появлением заряда такой же величины, но противоположного знака на другом теле. Например, при трении стеклянной палочки о шелк заряжаются оба тела: палочка отрицательно, шелк положительно.
Таким образом, всякий процесс заряжения есть процесс разделения зарядов. Сумма зарядов тел при этом не изменяется, заряды только перераспределяются. Отсюда следует закон сохранения заряда – один из фундаментальных законов природы, сформулированный в 1747 г. Б. Франклином и подтвержденный в 1843 г. М. Фарадеем: алгебраическая сумма зарядов, возникающих при любом электрическом процессе на всех телах, участвующих в процессе всегда равна нулю. Или: суммарный электрический заряд замкнутой системы тел не изменяется.
Электрические заряды не существуют сами по себе, а являются внутренними свойствами элементарных частиц – электронов, протонов и др.
В 1914 г. американский физик Р. Милликен экспериментально установил, что электрический заряд дискретен. Заряд любого тела составляет
целое кратное от элементарного электрического заряда e 1,6 10 19 Кл. q ne ,
где n – целое число.
Электрон и протон являются соответственно носителями элементарных отрицательного и положительного зарядов.
Например, наша Земля имеет отрицательный заряд 6 105 Кл. Это установлено по измерению напряженности электростатического поля в атмосфере Земли.
Большой вклад в исследование явлений электростатики внес знаменитый французский ученый Ш. Кулон. В 1785 г. он экспериментально установил закон взаимодействия двух неподвижных точечных электри-
ческих зарядов в вакууме: сила F взаимодействия двух неподвижных точечных зарядов q1 и q2 в вакууме прямопропорциональна произведению
5
модулей зарядов и обратнопропорциональна квадрату расстояния r между ними.
F k |
|
|
q1 |
|
|
|
q2 |
|
, |
(1.1) |
|
|
|
|
|
||||||
|
|
|
|
|||||||
|
|
r2 |
|
|||||||
|
|
|
|
|
|
|||||
где k 4 1 0 коэффициент пропорциональности, зависящий от системы
|
|
|
8,85 10 12 |
Кл |
2 |
|
|
единиц; 0 |
электрическая постоянная |
0 |
|
|
. |
||
Н м |
2 |
||||||
|
|
|
|
|
|
||
Кулоновские силы существенны до расстояний порядка 10 15 м (нижний предел). На меньших расстояниях начинают действовать ядерные силы. Что касается верхнего предела, то он стремится к бесконечности.
Принципиальное отличие кулоновских сил от гравитационных состоит в том, что последние всегда являются силами притяжения.
Точечным зарядом ( q ) называется заряженное тело, размеры которого
пренебрежительно малы по сравнению с расстоянием до других заряженных тел, с которым оно взаимодействует.
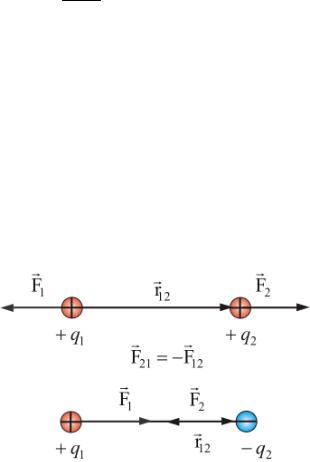
|
В |
электростатике взаимодей- |
|
ствие зарядов подчиняется тре- |
|
|
тьему закону Ньютона: силы взаи- |
|
|
модействия между зарядами рав- |
|
|
ны по величине и направлены про- |
|
|
тивоположно друг другу вдоль пря- |
|
|
мой, соединяющейзаряды(рис. 1.1). |
|
|
Если заряды не точечные, то |
|
|
закон |
Кулона нужно интегри- |
Рис. 1.1 |
ровать по объему. |
|
1.2. Электрическое поле. Напряженность электрического поля
Для понимания происхождения и передачи взаимодействия между зарядами, необходимо допустить наличие между ними какого-либо физического агента, обусловливающего это взаимодействие. Этим агентом является электрическое поле.
Вокруг заряда всегда есть электрическое поле, основное свойство которого заключается в том, что на всякий другой заряд, помещенный в это поле, действует сила.
6
Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.
Силовой характеристикой поля создаваемого зарядом q является
отношение силы действующей на заряд к величине этого заряда назы-
ваемое напряженностью электростатического поля, т.е.
E |
F |
|
q |
, |
(1.2) |
|
q |
4 0r2 |
|||||
|
|
|
|
где r расстояние от заряда q до точки поля, в которой определяют напря-
женность. |
|
|
|
Тогда F |
qE , при q 1 |
Кл, F |
E . |
Вектор напряженности электростатического поля равен силе,
действующей в данной точке на помещенный в нее пробный единичный положительный заряд.
Направление вектора напряженности определяет направление силы, действующей на положительный заряд, помещенный в рассматриваемую точку поля.
Из формулы (1.2) следует, что единица измерения напряженности электростатического поля – Н/Кл.
1 Н/Кл – напряженность такого поля, которое на точечный заряд 1 Кл действует с силой в 1 Н.
1.3. Принцип суперпозиции
Важнейшей задачей электростатики является оценка параметров поля при заданном, стационарном, распределении зарядов в пространстве. Один из способов её решения основан на принципе суперпозиции. Суть его в следующем.
Если поле создается несколькими точечными зарядами, то на пробный заряд q действует со стороны заряда qk такая сила, как если бы других
зарядов не было. Результирующая сила, действующая на заряд q , определится выражением:
|
|
|
F Fk . |
(1.3) |
|
|
|
k |
|
Выражение(1.3) – принципсуперпозицииилинезависимостидействиясил. |
||||
|
|
|
– результирующая напряженность поля в точке, где |
|
Т.к. F |
qE , то |
E |
||
расположен пробный заряд, так же подчиняется принципу суперпозиции: |
||||
|
|
|
|
|
E |
E1 |
E2 |
... Ek . |
(1.4) |
k
7
Это соотношение выражает принцип наложения или суперпозиции электрических полей и представляет важное свойство электрического поля.
напряженность результирующего поля, системы точечных зарядов равна векторной сумме напряженностей полей, созданных в данной точке каждым из них в отдельности.
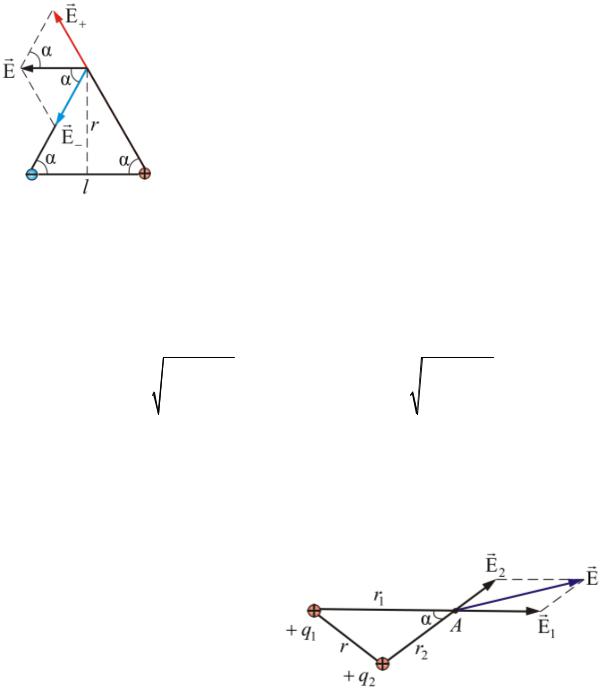
Рассмотрим применение принципа суперпозиции в случае поля, созданного электрической системой из двух зарядов. l расстояние между зарядами (рис. 1.2).
Поля, создаваемые различными зарядами, не
влияют друг на друга, поэтому вектор E результирующего поля нескольких зарядов q1,q2 ,q3,... может
быть найден по правилу сложения векторов (правило параллелограмма).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рис.1.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
E1 |
E2 |
E3... |
Ek . |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|||||
В случае двух зарядов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
и |
d |
E |
|
0 , так как задача симметрична. |
|||||||||||||||||||||||
E |
E |
E |
|
, |
|
E |
|
|
E |
|
|
|
|
x |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В данном случае |
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
E |
|
E |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
cos |
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
4 0 |
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
4 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
1 |
|
|
|
|
|
ql |
|
. |
|
|
|
|
|
|
(1.5) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 0 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
l2 |
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
4 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим |
другой |
пример. |
|
|||
Найдем |
напряженность |
электро- |
|
|||
статического поля E , создавае- |
|
|||||
мого |
двумя |
положительными |
|
|||
зарядами q1 и q2 в точке A , |
|
|||||
находящейся на расстоянии r1 от |
|
|||||
первого и r от второго зарядов |
|
|||||
|
2 |
|
|
|
|
|
(рис. 1.3). |
|
|
|
|
|
|
|
|
E1 |
q1 |
; |
||
|
|
4 r2 |
|
|||
|
|
|
0 1 |
|
|
|
|
|
|
Рис.1.3 |
E2 |
q2 |
|
. |
4 |
r2 |
||
|
0 |
2 |
|
8

Воспользуемся теоремой косинусов:
E |
E |
2 |
E |
2 |
2E E |
|
1 |
|
q2 |
|
q2 |
|
2q q |
|
|
|
|
cos |
|
|
1 |
|
2 |
|
1 |
2 |
cos , (1.6) |
||||
|
|
4 |
|
r2r2 |
|||||||||||
|
1 |
|
2 |
1 2 |
|
0 |
r4 |
|
r4 |
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
1 |
2 |
|
|
где cos r12 r22 r2 .
2r1r2
Если поле создается не точечными зарядами, то используют обычный в таких случаях прием. Тело разбивают на бесконечно малые элементы и определяют напряженность поля создаваемого каждым элементом, затем интегрируют по всему телу:
E d E , |
(1.7) |
где d E – напряженность поля, обусловленная заряженным элементом. Интеграл может быть линейным, по площади или по объему в зависи-
мости от формы тела. Для решения подобных задач пользуются соответствующими значениями плотности заряда:
dqdl – линейная плотность заряда (Кл/м);
dSdq – поверхностная плотность заряда Кл/м2;
dVdq – объемная плотность заряда Кл/м3.
Например, определим напряженность электрического поля в точке A (рис. 1.4) на расстоянии x от бесконечно длинного, линейного, равномерно распределенного заряда. Пусть – заряд, приходящийся на единицу длины.
Будем считать, что x мало по сравнению с длиной проводника. Выберем систему координат так,
чтобы |
ось у совпадала с провод- |
|||||||
ником. Элемент длины dy , несет |
||||||||
заряд |
dq dy . |
Создаваемая |
этим |
|||||
элементом напряженность |
|
электри- |
||||||
ческого поля в точке A : |
|
|
|
|||||
Рис.1.4 |
1 |
|
|
dy |
|
|
|
|
|
dE |
|
|
|
|
. |
(1.8) |
|
|
4 0 |
x2 y2 |
|
|||||
9

Вектор |
d E имеет проекции |
dEx и dEy , причем |
dEx dE cos , |
||||||
dEy dE sin . Т.к. |
проводник |
бесконечно длинный, |
а |
задача симмет- |
|||||
ричная, то |
у компонента вектора d E обратится в |
ноль (скомпенси- |
|||||||
руется), т.е. Ey dE sin 0 . |
|
|
|
cos dy . |
|
|
|||
Тогда E Ex |
|
dE cos |
|
|
|
||||
|
4 |
0 |
|
|
|||||
|
|
|
x2 y2 |
|
|
||||
Выразим у через . Т.к. y x tg , то dy cosxd2 и x2 y2 cosx22 , тогда
|
|
|
|
x |
|
|
|
|
E |
|
1 |
|
2 |
cos d |
|
. |
(1.9) |
|
|
2 0 x |
||||||
|
4 0 x x |
|
|
|||||
|
|
|
|
2 |
|
|
|
|
Таким образом, напряженность электрического поля линейно распределенных зарядов изменяется обратно пропорционально расстоянию до заряда.
Этот результат, полученный для бесконечно длинного линейного заряда, с хорошей точностью справедлив и для линейного заряда конечной длины при условии, что x мало по сравнению с расстоянием от точки A до концов проводника.
Если же поле создано сложными по форме заряженными телами и неравномерно заряженными телами, то используя принцип суперпозиции,
трудно рассчитать результирующее поле.
В формуле (1.7) d E – векторная величина:
|
|
1 |
dq r |
|
|
||
d E |
|
|
r2 |
|
, |
(1.10) |
|
4 0 |
r |
||||||
|
|
|
|
||||
так что интегрирование может оказаться непростым. Поэтому для вычис-
ления E часто пользуются другими методами, которые будут рассмотрены позже. Однако в некоторых, относительно простых случаях эти формулы
позволяют аналитически рассчитать E .
10
