Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1750

.pdf

Скачиваний:

Добавлен:

16.06.2024

Размер:

2.88 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

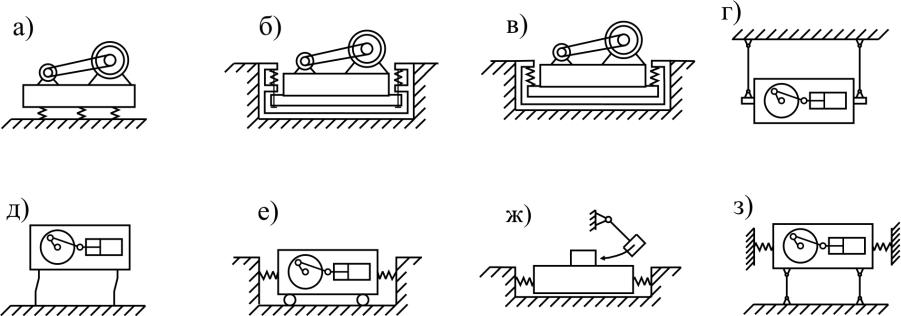
Рис. 1.20. Конструктивные схемы виброизоляции:

а – опорный вариант; б – подвесной вариант с пружинами, работающими на сжатие; в – то же, на растяжение; г – подвесной вариант с шарнирными стержнями;

д – опорный вариант со стержнями, работающими на изгиб; е – вариант с применением катков; ж – вариант с использованием слоя смазки; з – схема астатического маятника

Наиболее простым представляется рассмотрение виброизолированного объекта как системы с одной степенью свободы при гармонических колебаниях самого объекта или его основания. Эффективность виброизоляции в этом случае можно оценивать коэффициентом передачи μ, который при силовой виброизоляции равен отношению амплитуды силы, передающейся через податливые пружины (виброизоляторы) на основание, к амплитуде силы, действующей на виброизолированный объект, а при кинематической виброизоляции - отношению амплитуды перемещений виброизолированного объекта к амплитуде перемещений основания. В обоих случаях его величина равна

1/ 2 1,

(1.109)

где α=f0/f есть отношение частоты f0 вынужденных колебаний к частоте f собственных колебаний виброизолированного объекта. Очевидно, при достаточно большом значении α коэффициент μ очень мал.

Широкое практическое применение имеет линейная теория виброизоляции при возмущениях детерминированного характера. Возмущения считаются либо гармоническими, либо квазигармоническими (с медленно меняющимися амплитудой и частотой), либо импульсивными. В основу теории виброизоляции положен так называемый метод динамических жесткостей.

1.6.2. Динамические гасители

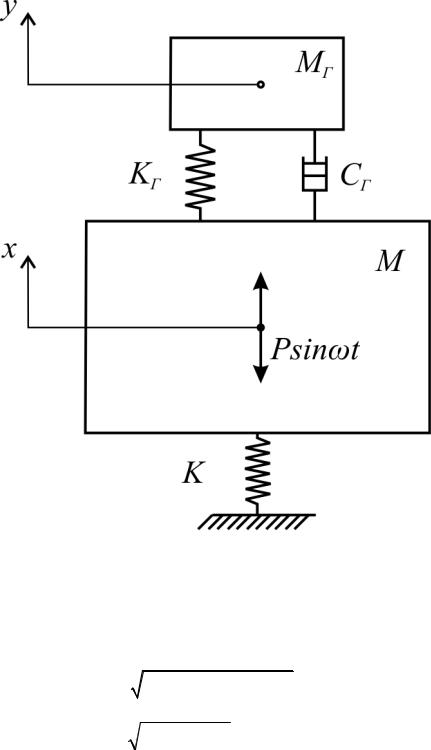
Рассматривается система (рис. 1.21), имеющая массу M и жесткость k. На системе установлен динамический гаситель колебаний, имеющий массу MГ, жесткость kГ и коэффициент демпфирования сГ. Система приводится в колебательное движение возмущающей силой Psinωt [46].

Дифференциальные уравнения колебаний системы с гасителем имеют вид:

x 2n(x y) ( p2	vГ2 )x vГ2 y	P	sin t;
x 2n(x y) ( p2	vГ2 )x vГ2 y	M	sin t;	(1.110)
		M		(1.110)
2	( y x) 0,
y 2nГ ( y x) pГ	( y x) 0,
	62

где

2n c / M ; p2 k / M ; v2							k	Г	/ M ;
Г						Г				(1.111)
2n	c	/ M		; p2	k		/ M		.
			Г			Г		Г
Г	Г			Г

Рис. 1.21. Схема динамического гасителя колебаний с затуханием

Решение, соответствующее установившимся колебаниям, имеет вид

1		( f 2 g2 )2	4h2 g2 sin t;
	A
			(1.112)
1
		f 2 4h2 g2	sin t.
	A

		63

где

( f

)(1 g

) f

2 2

(1 g

)

;

x / x

; y / x ;

P / Mp2 ; f

/ p;

(1.113)

ст

g / p; MГ / M ; h cГ / cК; cK 2MГ p;

здесь p и pГ – круговые частоты собственных колебаний соответственно системы (при отсутствии гасителя) и гасителя (при неподвижной массе M); cК – коэффициент критического затухания.

1.6.2.1. Динамический гаситель без затухания

Если затухание в гасителе настолько мало, что может не учитываться в расчете, то принимают сГ=0. Главная масса М не будет колебаться в случае, если f=g, т.е. круговая собственная частота рГ присоединенного гасителя будет равна круговой частоте ω изменения возмущающей силы. В этом случае

1/ f 2

k / k Г или ykГ P,

(1.114)

т.е. упругая сила гасителя во всякий момент времени будет уравновешивать возмущающую силу. Это справедливо для любого значения отношения g.

Поскольку применение гасителя особенно эффективно в случае, если система находится в состоянии резонанса или, по крайней мере, близка к нему, то полагаем p=pГ, откуда kГ/k=MГ/M=μ. Значение μ должно быть таким, чтобы амплитуда колебаний массы MГ гасителя, равная P/MГω2, была в пределах, допускаемых прочностью пружины гасителя.

Частотное уравнение системы с гасителем как системы с двумя степенями свободы при f=1 будет

g4 (2 )g2		1 0.		(1.115)
Корни этого уравнения
g2	1	1	.	(1.116)
1,2	2
	2		4
	64

При небольших значениях μ частоты собственных колебаний системы с гасителем мало отличаются одна от другой и от расчетного значения ω=p – круговой частоты возмущающей силы, равной круговой частоте собственных колебаний системы. Поэтому применение динамического гасителя без затухания связано с требованием строгого постоянства частоты возмущающей силы.

1.6.2.2. Динамический гаситель с затуханием

Часто затухание оказывается полезным для работы гасителя и поэтому его вводят, снабжая гаситель специальными устройствами. Тогда возникает вопрос о рациональном подборе параметров затухания.

При резонансе, т.е. при f=1, как в случае очень малого затухания (сГ→0), так и в случае очень большого затухания, когда обе массы оказываются жестко взаимосвязанными (сГ→∞), амплитуды колебаний системы неограниченно возрастают. Между этими предельными значениями сГ имеется такое его значение, при котором резонансная амплитуда минимальна.

Имеются определенные значения g, при которых можно так настроить гаситель, что амплитуда колебаний системы не будет зависеть от затухания в гасителе. Такой гаситель называется гасителем с наилучшей настройкой. В этом случае для настройки на любую величину массы гасителя должно выполняться условие

f 1/(1 ),

(1.117)

при этом амплитуда колебаний системы будет

1 2 / .

(1.118)

Если гаситель колебаний имеет постоянную настройку f=1, то

	g2 1	/(2 );		(1.119)
1/	(1 )	/(2	) .	(1.120)

В этом случае гаситель называется настроенным на частоту системы. Затухание, удовлетворяющее условию наилучшего действия гасителя, может быть определено с помощью специальных графиков.

Амплитуду относительного движения масс М и МГ, определяющую напряжение в пружине гасителя, вычисляют по формуле

				2 / 2 gh.	(1.121)

1.6.3. Ударные гасители

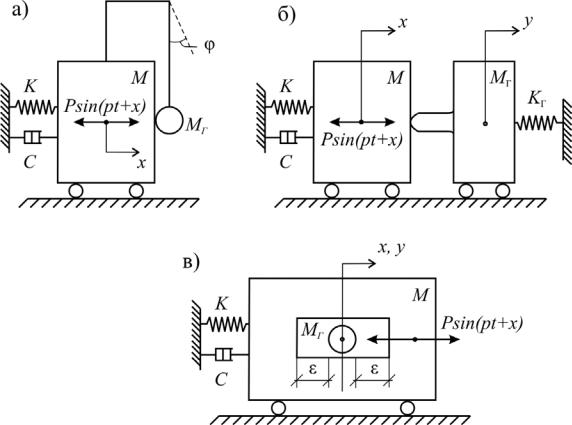
Рассмотрим маятниковые, пружинные и плавающие гасители (рис. 1.22), установленные на системе, имеющей массу М, жесткость k и коэффициент затухания c. Система приводится в колебательное движение возмущающей силой Psinωt. Введем следующие обозначения: МГ – масса гасителя; δ(t–RT) – дельта-функция, r – коэффициент восстановления скорости при ударе; Т – период соударений.

Рис. 1.22. Схемы ударных гасителей колебаний

1.6.3.1. Маятниковый ударный гаситель

Дифференциальные уравнения установившихся колебаний системы и присоединенного к ней маятникового гасителя (рис. 1.22, а) длиной l имеют вид:

где

2nx p2

pГ2

	P			S
x		sin( t )			(t RT );
	M0			M0
					R 0	(1.122)
x	S

			(t RT ),
l
	MГl R 0


2n c / M	; p2			k /	M		;
0					0
pГ2 g / l; M0 M MГ;								(1.123)
pГ2 g / l; M0 M MГ;								(1.123)
		M0 MГ
		M0 MГ
S (1 r)						l (T ).
S (1 r)		M	0	M		l (T ).
			0		Г

Резонансные колебания системы и гасителя для интервала времени (0, Т) при выполнении условий настройки

T 2 ;2 pГ

(1.124)

и условия равенства нулю отклонения системы и гасителя во время соударения имеют вид:

а) если затухание в системе не учитывается, т. е. n=0, то

1			3
					pt sin pt			2 cos pt ;
2		4d( , r)
								3	(1.125)
2			3	2		pt	3

					sin			pt sin pt ;
3	2					2	4d( , r)

б) если затухание в системе учитывается, то

						1											2			2(1 2 ) (1 r)(1 )
																	2			2(1 2 ) (1 r)(1 )
			C			2						4
			C			2						4
	8 (1 r)													(2			t )
	8 (1 r)													(2			t )
									e													sin t (1 r) cos t ;
	3(e			2	1)				e													sin t (1 r) cos t ;
	3(e				1)
						4																							4(1 )																	3/ 4							2					t
																																																					2

																	1							r																																sin
								2									1							r																			(3/ 4					2	)		2				2	sin		2
		3C								4																																	(3/ 4						)									2
		3C								4
				(1 r)																					t
				(1 r)															cos						t			2 2(1 2 ) (1 r)(1 )
																									2
	(3/ 4 2 )2												2												2
																																										(2 t )
(1 r) (1															2		)(3/ 4											2		)				4				2	2e			(2 t )
(1 r) (1																	)(3/ 4													)				4					2e								sin t
											(3/ 4 2 )2 2																													e2					1

	(1 r)								e		2						(2e				t
											2										t
																									1) 1
																																					cos			t ,
	3/ 4								2					2						2				(e		2											cos			t ,
	3/ 4																							(e						1)



где
							x			;								l					; x												P				;					MГ			;
							x											l																	P									MГ

							xст											xст								ст						M0 p												M0
							xст											xст														M0 p												M0
																	(1 r)																		2					2					2
																	(1 r)																		2					2					2
			d( , r) (1 )(1 r) ;																																		p				n ;
			d( , r) (1 )(1 r) ;																																		p				n ;
						n							2																																								2						2
						n							2																																								2						2
								; C								4				2(1 2 ) (1 r)(1 )																																		(1 r)						;
								; C								4				2(1 2 ) (1 r)(1 )																																		(1 r)						;

																																	2
																														e			2					1;

							(3/ 4 2 )2 2
							(3/ 4 2 )2 2																								e2 1										2					2(1						)(3/ 4						) 9
																	1													1						3					2					2(1						)(3/ 4						) 9
																																																		2							2		2
																																																						2						.
							(3/ 4											2		)		2					2				4					4																	e	2		1				.
							(3/ 4													)											4					4																	e			1

(1.126)

(1.127)

1.6.3.2. Пружинный ударный гаситель

Дифференциальные уравнения установившихся колебаний системы и пружинного ударного гасителя (рис. 1.22, б), имеющего жесткость kГ:

где

			P		S
2nx p2 x			P	sin( t )	S	(t
2nx p2 x			M	sin( t )		(t
			M		M R 0
	S
pГ2 y	S	(t RT ),
pГ2 y		(t RT ),
	M0 R 0


2n	c	; p2		k	; p2		kГ	;
2n		; p2			; p2			;
	M			M		Г	MГ
	M			M			MГ
			MMГ
S (1 r)			MMГ			x(T ) y(T ) .
S (1 r)						x(T ) y(T ) .
			M MГ
			M MГ

RT );

(1.128)

(1.129)

Резонансные колебания системы и гасителя для интервала времени (0, Т) при выполнении условий настройки (1.124) и условия равенства нулю отклонения системы и гасителя во время соударения описываются формулами:

а) если затухание в системе не учитывается, т.е. n=0, то

1

2

	d( , r)
sin		pt	;
		2

pt sin pt;

б) если затухание в системе учитывается, то

1					(1 r)			(2 t )
1				1	(1 r)		e 2				sin t;
	2	4		1	1 (1 r)N		e 2			1	sin t;
	2	4			1 (1 r)N			e		1
1					1 r			t
1					1 r	sin		t	,
		2				sin			,
2		2	4 1 (1 r)N					2
2			4 1 (1 r)N					2

(1.130)

(1.131)

где

;

; MГ

; d( , r)

(1 r)

;

xст

ст

(1 )(1 r)

(1.132)

;

; N 1/ 2

/(e

1).

1.6.3.3. Плавающий ударный гаситель

Дифференциальные уравнения установившихся колебаний системы и плавающего ударного гасителя (рис. 1.22, в), встроенного с зазорами ε, имеют вид:

						P		S
x 2nx p2 x						P	sin( t )	S	( 1)R (t RT );
x 2nx p2 x							sin( t )		( 1)R (t RT );
					M			M R 0		(1.133)
	S									(1.133)
	S			R
y			( 1)			(t RT ),
y	M		( 1)			(t RT ),
	M	0 R 0

где

2n	c	; p2			k	;


	M				M
S (1 r)				MMГ				x(T ) y(T )	при (0 t T ),	(1.134)

				M MГ
S (1 r)				MMГ			x(2T ) y(2T )
									при (T t 2T ).
			M MГ

Резонансные колебания системы и гасителя для интервала времени (0, 2Т) при выполнении условия настройки

(1.135)

и условий равенства нулю отклонения системы и равенства величине ε перемещения гасителя описываются формулами:

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.06.20242.85 Mб01746.pdf
#
16.06.20242.85 Mб01747.pdf
#
16.06.20242.86 Mб01748.pdf
#
16.06.20242.86 Mб01749.pdf
#
16.06.2024214.87 Кб0175.pdf
#
16.06.20242.88 Mб01750.pdf
#
16.06.20242.88 Mб01751.pdf
#
16.06.20242.89 Mб01752.pdf
#
16.06.20242.89 Mб11753.pdf
#
16.06.20242.9 Mб01754.pdf
#
16.06.20242.9 Mб01755.pdf