1625

221

222

223

Пример выполнения контрольной работы

Исходные данные

1=0,001 ч-1

2= 3= 4= 5=0,1 ч-1

6= 7=0,01 ч-1

8= 9= 10= 11=0,2 ч-1

12= 13= 14= 15=0,5 ч-1

=50 %

Рис. I. Исходная структурная схема надежности системы

Преобразуем исходную схему, заменив ее элементы квазиэлементами. Преобразованная схема представлена на рис. II.

Рис. II. Преобразованная схема

224

Продолжение прил. 2

Элемент А преобразованной схемы заменяет элементы 2 и 3 исходной схемы. Учитывая, что P2=P3, а элементы 2 и 3 соединены параллельно, вероятность безотказной работы элемента А равна:

Элементы 4 и 5 также образуют параллельное соединение, заменив которое элементом В и учитывая, что P4=P5, получим:

Элементы 6 и 7 в исходной схеме соединены последовательно.

Элементы 10 и 11 с параллельным соединением заменяем элементом Е.

Элементы 12, 13, 14 и 15 образуют соединение “2 из 4”, которое заменяем элементом F. Так как P12=P13=P14=P15, то для определения вероятности безотказной работы элемента F можно воспользоваться комбинаторным методом (см. подразд. 3.3):

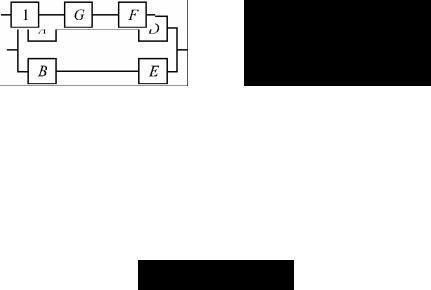
Элементы A, B, C, D и Е образуют (см. рис. II) мостиковую систему, которую можно заменить элементом G. Для расчета вероятности безотказной работы воспользуемся теоремой о разложении функции логики по одному аргументу. В качестве особого элемента выберем элемент С, так как в этом случае мостиковая схема преобразуется в наиболее простые схемы надежности. Тогда

225

Продолжение прил. 2

Рис. III. Структурные схемы надежности мостиковой схемы (рис. II) при абсолютно надежном (а) и отказавшем (б) элементе С

Учитывая, что PA=PB, PD=PE, получим:

PG=PC [1–(1– PA)(1– PB)] [1–(1– PD)(1– PE)]+

+(1– PC)[1-(1– PAPD) (1– PBPE)]=

=PC [1–(1– PA)2] [1–(1– PD)2]+(1– PC)[1-(1– PAPD)2] (8)

Полученная в результате преобразований схема изображена на рис. IV.

Рис. IV. Преобразованная структурная схема надежности

Так как по условию все элементы системы работают в период нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 подчиняются экспоненциальному закону:

Результаты расчетов вероятностей безотказной работы элементов 1–15 исходной схемы по формуле (10) для наработки от 0 до 3·106 часов представлены в табл. II.

Результаты расчетов вероятностей безотказной работы элементов A, B, C, D, E, F и G по формулам (1)...(6) и (8) также приведены в табл. II.

14.На рис. V показан график зависимости вероятности безотказной работы системы PS от времени (наработки) t.

15.По графику (см. рис. V, кривая PS) находим для =50 % -про- центную наработку системы T =1,9·106 ч.

Проверочный расчет при t=1,9·106 ч показывает (см. табл. II), что

PS 0,5.

17.По условиям задания требуется обеспечить -процентную наработ-

ку системы до отказа треб=1,5T =1,5·1,9·106=2,85·106 ч.

18.Расчет показывает (см. табл. II), что при t=2,85·106 ч для элементов

преобразованной схемы (см. рис. IV) P1=0,9972, PG=0,9594 и PF=0,2458.

Следовательно, из трех последовательно соединенных элементов мини-

226

Продолжение прил. 2

мальное значение вероятности безотказной работы имеет элемент F и именно увеличение его надежности даст максимальное увеличение надежности системы в целом.

20. Для определения минимально необходимых вероятностей безотказной работы P12над... P15над элементов 12...15 необходимо решить уравнение

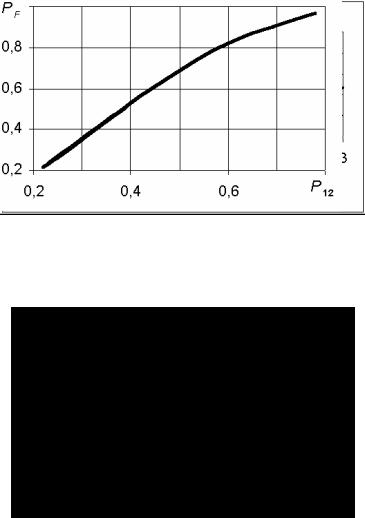
(6) относительно P12 при PF=0,5226. Так как аналитическое решение этого уравнения связано с определенными трудностями, целесообразнее использовать графоаналитический метод определения P12. Для этого по данным табл. II строим график зависимости PF=f(P12), представленный на рис. VI. По графику при PF=0,5226 находим P12над 0,4.

Таблица I I Вероятности безотказной работы системы и ее элементов

227

Продолжение прил. 2

Рис. V. Вероятности безотказной работы исходной системы (РS), системы, состоящей из элементов с повышенной надежностью (РSнад), и системы со структурным резервированием элементов (РSрез)

Рис. VI. Зависимость вероятности безотказной работы квазиэлемента F от вероятности безотказной работы его элементов

Так как по условиям задания все элементы работают в период нормальной эксплуатации и подчиняются экспоненциальному закону (см. (10)), то для элементов 12...15 при t=T треб=2,85·106 ч-1 находим

Таким образом, для увеличения -процентной наработки системы до отказа необходимо снизить интенсивность отказов элементов 12, 13, 14 и 15 с 0,5 до 0,322·10-6 ч-1.

Результаты расчетов для системы с увеличенной надежностью элементов 12, 13, 14 и 15 приведены в табл. II. В частности, там приведены расчетные значения вероятности PFнад безотказной работы элемента F и

228

Продолжение прил. 2

системы в целом PSнад, полученные в результате повышения надежности элементов 12...15. При t=2,85·106 ч вероятность безотказной работы

системы PSнад (T треб)=0,5011, что соответствует условиям задания. График

PSнад(t) приведен на рис. V.

Для второго способа увеличения вероятности безотказной работы системы – структурного резервирования – по тем же соображениям также выбираем элемент F, вероятность безотказной работы которого после резервирования должна быть не ниже 0,5226 (см. формулу (11)).

Для элемента F структурное резервирование означает увеличение общего числа элементов. Аналитически определить минимально необходимое количество элементов невозможно, т.к. число элементов должно быть целым и функция PF=f(n) дискретна.

Для повышения надежности системы “2 из 4” добавляем к ней элементы, идентичные по надежности исходным элементам 12...15, до тех пор, пока вероятность безотказной работы элемента F не достигнет заданного значения.

Добавляем элемент 16, получаем квазиэлемент Fрез, представляющий собой систему типа “2 из 5”:

Так как PFрез>0,5226, полученная система (рис. VII) удовлетворяет требованиям задания (при t=T треб PSрез>0,5, что соответствует условию задания).

Результаты расчетов вероятностей безотказной работы системы типа “2 из 7” PFрез и системы в целом PSрез представлены в табл. II.

229

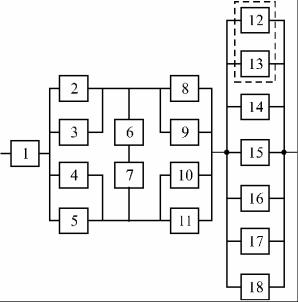
Окончание прил. 2

Рис. VII. Структурная схема системы после структурного резервирования

На рис. V показаны кривые зависимостей вероятности безотказной работы системы после повышения надежности элементов 12...15 (кривая PSнад) и после структурного резервирования (кривая PSрез).

Выводы:

1.На рис. V представлена зависимость вероятности безотказной

работы системы (кривая PS). Из графика видно, что 50-процентная наработка исходной системы составляет 1,9·106 часов.

2.Для повышения надежности и увеличения 50-процентной наработки системы в 1,5 раза (до 2,85·106 часов) предложено два метода:

а) повышение надежности элементов 12, 13, 14 и 15 путем уменьшения интенсивности их отказов с 0,5·106 до 0,322·106 ч-1;

б) нагруженное резервирование основных элементов 12 и 13 идентичными по надежности резервными элементами 14, 15, 16, 17 и 18

(см. рис. VII).

По вероятности безотказной работы модернизированной системы вто-

рой метод предпочтителен, так как кривая PSрез (см. рис. V) располагается выше кривой PSнад.

230