1572
.pdf
Тогда для параметра 1 |
будем иметь: |
|
|
||
|
ν 2t |
* |
2ν R |
2h |
g . |
1 |
|
||||
0 |
|
0 |
|
|
|
Для второго «отскока», соответственно, получим:
h |
4 |
h; |
|
2ν R |
2 |
2h |
g . |
R |
2 |
|
|||||
2 |
|
|
0 |
|
|
|
(3.29)
(3.30)
Поскольку длина i-ого участка движения тела с отскоком будет равна:
|
|
2 R |
i |
2h |
g , |
|
|
|
|
|
|
|
i |
0 |
|
|
|
(3.31)
то общая длина L2 траектории движения осколка с отскоками будет равна сумме геометрической прогрессии:
|
|
|
|
|
|
R Rn 1 |
|
L2 2ν0 Ri |
2h |
g 2ν0 |
2h |
g |
R 1 . |
||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перейдя к пределу и учитывая, чтоR<1, получим из (3.32):
L |
2ν |
2h |
g R 1 R . |
|
2 |
0 |
|
|
|
(3.32)
(3.33)
Длину участка L3 из рис. 3.7 определим, исходя из теоремы об изменении кинетической энергии движущегося тела:
ν |
2 |
2 |
fgL |
, |
|
||||
0 |
|
|
3 |
|
(3.34)
где f – коэффициент трения скольжения осколка стекла по дорожному полотну. Тогда горизонтальная проекция общей длины траектории движения отделившейся относительно дорожного полотна на высоте h осколка стекла, опре-
деляется выражением:
1 |
2 |
3 |
|
0 |
|
|
|
|
|
|
1 R |
1 R |
|
(3.35) |
L L L а |
|
ν |
|
2H |
2h |
|
g |
|
, |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где h, H – соответственно расстояния от полотна дороги до нижней и верхней кромки разбитого стекла, м.
Скорость автомобиля в момент столкновения, при котором разбилось стекло, тогда будет равна:
|
|
1 R |
|
|
|
|
1 R . |
|
ν0 а |
g |
2H |
2h |
(3.36) |
||||
|
|
|
|
|
|
|
|
|
При столкновении автомобилей стёкла разбиваются на множество осколков, поэтому зона расположения осколков разбитого стекла, например фары, будет представлять собой эллипс, одна из осей которого коллинеарна вектору скорости автомобиля в момент столкновения, а её длина может быть определена по формуле (3.35). Величина параметра «а» легко определяется (измеряется) при проведении экспертизы на месте аварии.
61
Формула (3.36) получена без учёта потерь энергии, а, соответственно, и скорости столкновения автомобиля, на деформацию элементов машины в результате столкновения, и фактически определяет начальную скорость движения осколков стекла. Тем не менее, формула (3.36) позволяет определять скорость автомобиля в момент столкновения без изменения коэффициентов скольжения колёс автомобиля, разбившего стекло, с дорогой [9].
Вычислим потери на сопротивление воздуха с учётом рода отделяющихся материалов и реальных размеров частиц [79].
В основу расчётов положен известныё из элементарной физики принцип о том, что при полёте частицы в воздушной среде сумма силы инерции частицы Fин и силы сопротивления движению Fсопр равна нулю:
F |
F |
0, |
||
ин |
сопр |
|
|
|
при этом |
m dν |
dt , |
||
F |
||||
ин |
|
|
|
|
F |
kAρ ν |
2 |
2, |
|
|
||||
сопр |
|
|
|
|
где m – масса частицы, кг;
v – скорость её движения, м/с; t – время, с;
k – коэффициент аэродинамического сопротивления; A – лобовая площадь поверхности частицы, м2;
ρ – плотность воздуха, кг/м3.
Подставив соотношения (3.38) и (3.39) в (3.37), имеем:
(3.37)
(3.38)
(3.39)
m dν dt kAρ ν |
2 |
2. |
|
(3.40)
В случае если в качестве индикатора скорости используется осколок стекла толщиной δ и средней лобовой поверхностью A, с учётом того, что
m Aδ ρст , |
(3. |
|
41) |
||
|
(ρст – плотность стекла), выражение ющее:
dν
dt
откуда
(3.40) может быть преобразовано в следу-
kρ ν |
2 |
2δ ρст , |
(3.42) |
|
dν ν2 kρ dt 2δ ρст . |
(3.43) |
Последнее соотношение можно интегрировать:
62
ν |
ν |
|
kρ |
t |
dν |
2 |
2δ ρст dt, |
||
|
|
|
|
|
ν |
|
|
|
0 |
0 |
|
|
|
|
(3.44)
причём, после интегрирования и ряда несложных преобразований имеем текущее значение скорости полёта частицы:
ν 2ν δ ρ |
ст |
2δ ρ |
ст |
ν kρ t . |
0 |
|
0 |
Используем последнее соотношение с учётом того, что упрощения дальнейших записей введём обозначение
ν dx
dt,
(3.45)
и для
B kρ |
2δ ρ |
ст |
, |
|
|
|
|
|
|
|
|
тогда |
|
|
|
|
|
dx dt |
1 ν |
Bt |
. |
||
|
0 |
|
|
|
|
Последнее уравнение можно интегрировать по частям:
(3.46)
(3.47)
x |
|
t |
|
0 |
|
|
|
|
dx |
|
Bt |
|
|||
|
1 |
|
ν |
|
dt, |
||
0 |
|
0 |
|
|
|
|
|
что приводит к следующему результату
x |
|
|
|
Btν |
|
|
1 B |
|
ln 1 |
|
. |
||
|
|
|
|
0 |
|
|
(3.48)
(3.49)
Определим общую длину траектории движения отделившейся относительно дорожного полотна на высоте h части автомобиля, в качестве которой может быть и осколок стекла, с учётом выражений (3.22), (3.33) и (3.49), получим:
L 1 |
B ln 1 Bν0t1 1 B ln 1 Bν0t2 1 B ln 1 Bν0t1 1 Bν0t2 , |
(3.50) |
|
где t1 |
– |
время движения частицы по первому участку, с; |
|
t2 |
– |
время движения частицы по второму участку, с. |
|
С учётом того, что
t |
|
2h g , |
1 |
|
|
|
|
|
|
|
|
R |
|
2h g K |
2h g Kt |
|
t |
2 |
|
2R |
1 |
|
, |
||||
|
|
|
|
|
|
|
|
1 |
|
где K 2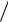R
1 R ,
выражение (3.50) примет вид:
L1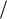
B ln 1 Bν0Kt1 Bν0t1 B2ν02Kt12
1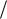
B ln 1 Bν0t1 K 1 B2ν02Kt12 .
Обозначив K K 1, из формулы (3.53) получим:
(3.51)
(3.52)
(3.53)
63
L 1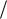
B ln 1 Bν0t1K B2ν02t12 K .
Преобразуем выражение (3.54):
|
2 |
ν |
2 |
t |
2 |
K Bν t |
K 1 e |
LB |
, |
||||
B |
|
|
|
||||||||||
|
|
|
0 |
|
|
1 |
0 1 |
|
|
|
|
||
получим квадратное уравнение: |
|
|
|
|
|
|
|
|
|
|
|||
2 |
ν |
|
2 |
t |
2 |
K Bν t K 1 e |
LB |
0. |
|||||
B |
|
|
|
|
|
||||||||
|
0 |
|
1 |
|
|
|
0 1 |
|
|
|
|
||
(3.54)
(3.55)
(3.56)
Для упрощения дальнейших записей введём следующие обозначения:
2 |
t |
2 |
K; |
b Bt K ; |
c 1-e |
LB |
, |
||
z B |
|
|
|||||||
|
1 |
|
|
1 |
|
|
|
|
|
тогда формула (3.56) примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
zν |
2 |
bν |
c |
0. |
|
|
|
|
|
|
|
|
||||
|
|
|
0 |
|
0 |
|
|
|
|
(3.57)
(3.58)
Корнем уравнения (3.58), а следовательно, и скорость автомобиля в момент столкновения, при котором разбилось стекло, будет выражение:
0 |
|
|
b |
|
2 |
4zc |
|
|
ν |
|
b |
|
|
2z. |
(3.59)
Полученное выражение имеет теоретический интерес для анализа влияния действующих параметров (ρ, ρст, k, δ, t1 и t2) на скорость движения частицы. Кроме того, данное выражение учитывает потери на сопротивление воздуха с учётом рода отделяющихся материалов и реальных размеров частиц, что позволяет уточнить значение скорости автомобиля в момент, предшествующий ДТП (столкновение, наезд на неподвижное препятствие и др.).
3.5. Модели определения скорости транспортных средств
Авторами [51] рассмотрена возможность установления механизма ДТП, а именно:
1)с определением скоростей двух столкнувшихся транспортных средств до удара, в момент удара и в процессе отбрасывания после удара;
2)c определением потерь кинетической энергии при ударе;
3)с определением ударного импульса и ударной силы.
В современной практике проведения судебных автотехнических экспертиз используются различные способы определения скоростей движения транспортных средств в момент столкновения.
Существует метод определения скорости движения автомобиля в момент столкновения при некоторых ограничениях, накладываемых на условия ДТП, таких, например, когда известны скорость движения автомобиля до торможения и длина следа скольжения до момента наезда [36], а также разновидность этого метода, когда к двум упомянутым ограничениям добавляется третье, а
64
именно известное установившееся замедление автомобиля при его торможении [96]. Применение этих методов весьма ограничено, поскольку на практике эксперт довольно часто имеет дело со случаями, когда указанные условия не выполняются.
Кроме того, эти методы обладают существенным недостатком: они игнорируют факт ударного взаимодействия двух столкнувшихся автомобилей, в результате которого они повреждаются и отбрасываются друг от друга, совершая при этом сложные движения.
Чтобы количественно оценить результаты повреждений, а по ним и скорость автомобиля при наездах различного вида, иногда определяют объем деформированной части автомобиля. Можно вычислить энергию, необходимую для такого деформирования и разрушения каким-либо способом, основанным на применении методов теории пластичности и механики деформируемого твердого тела [4, 5]. Далее ее можно сравнить с энергией, определенной при наезде автомобиля на плоскую жесткую поверхность в условиях полигонных испытаний, при которых фиксировалась скорость наезда, по которой производилась оценка скорости движения автомобиля при реальном столкновении [6]. Такой метод оценки скорости движения автомобиля связан с существенными материальными затратами, так как предполагает наличие спектра экспериментальных данных полигонных испытаний автомобилей при различных скоростях наезда. Кроме того, в принципе некорректно сравнивать работу деформаций при реальном столкновении двух автомобилей с энергией фронтального наезда автомобиля на абсолютно жесткую плоскость, что приводит к большим ошибкам в оценке реальной скорости движения автомобиля.
До настоящего времени отсутствует концепция, на основе которой могла бы быть разработана методика определения скоростей движения двух и более транспортных средств при их столкновении под произвольным углом с учетом основных факторов, влияющих на их величины.
Одним из основных этапов создания такой методики является математическое моделирование процесса перекрестного столкновения двух транспортных средств на основании применения элементарной теории удара и общих теорем динамики.
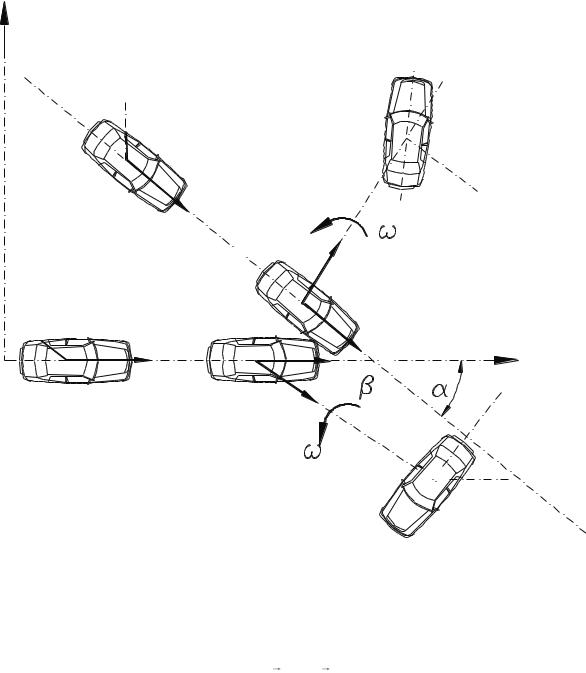
Пусть автомобили 1 и 2 движутся прямолинейно со скоростями V01
соответственно (рис. 3.10, положение автомобилей I). Перед столкновением они начинают тормозить, снижая величины скоростей до значений V1 и V2 , и
на этих скоростях входят в непосредственный контакт в точке А. То есть между движущимися автомобилями происходит удар (рис. 3.10, положение автомоби-
лей II).
Процесс удара принято разделять на две фазы [6, 10]. Первая фаза продолжается от момента соприкосновения тел до момента их наибольшего сближения. Вторая фаза продолжается от конца первой фазы до момента разделения тел.
65
При расчете ударов принимают следующие основные допущения [10]:
1.Во время удара обычными силами можно пренебречь, учитывая импульсы только ударных сил.
2.Перемещениями точек во время удара можно пренебречь, то есть в мо-
мент начала удара (начала первой фазы, |
t1 0 ) и |
(конец второй фазы, t2 ) точки соударяющихся положение, – длительность удара.
в момент окончания удара тел занимают одно и то же
Y
III
|
|
|
I |
a2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
02 |
|
V |
|
|
|
|
|
|
||
|
|
|
|
|
|
02 |
|
|
|
|
|
|
l |
|
|
|
|
|
|
02 |
|
|
|
I |
|
|
2 |
|
a |
|
|
|
|
|
|
1 |
|
V |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
01 |
|
C |
|
C |
|
|
l |
|
|
0 |
01 |
|
01 |
1 |
||
1 |
|
|
|
1 |
||
|
|
|
|
|
||
|
l 2 |
|
|
u |
|
|
2C |
|
C |
|
|
2 |
|
|
A |
|
|
|
V |
|
|
1 |
|
u |
l |
|
10 |
||
1 |
||
|
|
0 |
|
|
2K |
|
|
C |
|
|
I |
|
|
2 |
|
2 |
IIV |
2 |
|
||
20 |
|
|
V |
X |
2 |
10 |
|
|
1 |
IIV |
|
|
I |
1 |
|
|
|
C |
|
|
|
III |
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
1k |
|
Рис. 3.10. Схема расположения автомобилей при анализе механической системы «Автомобиль 1 – автомобиль 2»
3. Изменения скорости точки за время удара определяется уравнением
V |
1 |
S , |
(3.60) |
|
m |
||||
|
|
|
которое называют основным уравнением динамики точки при ударе. Это уравнение в расчете ударов играет ту же роль, что и уравнение
66
W |
1 |
F |
(3.61) |
|
m |
||||
|
|
|
в расчете движений точки под действием обычных сил. В уравнениях (3.60) и (3.61) введены следующие обозначения:
V – |
изменение скорости точки; |
m |
масса точки; |
S |
ударный импульс; |
W |
ускорение точки; |
|
|
F |
обычная сила. |
|
Формула (3.61) может быть представлена в виде:
mV
S
.
(3.62)
То есть полученное за время удара количество движения равно ударному импульсу. Это уравнение соответствует второму закону Ньютона, только вместо ускорения необходимо подставить скорость, а вместо силы – ударный импульс. Таким образом, если сила сообщает массе ускорение, то ударный импульс – скорость.
Сформулированные допущения сохраняются и при расчете ударов механических систем и твердых деформируемых тел, в частности, двух рассматриваемых автомобилей.
В случае перекрестного столкновения между направлениями векторов V1 и V2 в первой фазе удара образуется угол .
Задаются системой координат XOY таким образом, чтобы ось OX совпала с направлением вектора V1 (рис. 3.10).
В результате соударения во второй фазе удара автомобили в общем случае резко меняют характер движения, а также величины и направления своих скоростей. Их поступательные движения переходят в плоские, которые представляют собой совокупности двух поступательных движений с начальными линейными скоростями U10 и U20 . С такими скоростями они разъединяются и
отбрасываются в разные направления на расстояния
l1
и
l2
, и вращательных с
начальными угловыми скоростями
10
и 20
, с которыми они разворачиваются
относительно осей, проходящих перпендикулярно плоскости движения через их
центры масс C |
и C |
2 |
, на углы |
и |
2K |
соответственно до своих полных оста- |
1 |
|
1K |
|
|
новок (рис. 3.10, положение автомобилей III).
В основу решения задачи положена энергетическая концепция, согласно которой подавляющая часть запаса кинетических энергий автомобилей в момент начала удара расходуется на работу по их перемещению при отбрасывании после удара и на работу по деформированию и разрушению их частей при ударе.
Рассматривается механическая система «автомобиль 1 – автомобиль 2» в процессе первой и второй фаз удара. Соотношение кинетических энергий объ-
67
ектов этой системы при ударе может Остроградского-Карно [55]:
T0
где
быть
T T *,
записано на основании теоремы
(3.63)
T |
1 |
(m V |
2 |
m V |
2 |
) |
||
|
||||||||
|
|
|
||||||
0 |
2 |
1 |
1 |
2 |
2 |
|
||
|
|
|
|
|
|
|
|
|
кинетическая энергия системы в момент начала удара (первая фаза):
(3.64)
T |
1 |
(m U |
|
J |
|
m U |
|
J |
|
|
) |
|
|
|
2 |
|
|
2 |
|
2 |
|
|
2 |
|
|
|
2 |
1 |
10 |
|
Z1 |
10 |
2 |
20 |
|
Z 2 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кинетическая энергия системы в момент конца удара (вторая фаза):
T* |
1 k |
[m (U |
|
V ) |
2 |
J |
|
2 |
m |
(U |
|
V ) |
2 |
J |
|
2 |
] |
|
10 |
|
|
20 |
|
Z 2 |
|
||||||||||
|
2(1 k) |
1 |
1 |
|
|
Z1 |
10 |
2 |
|
2 |
|
|
20 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.65)
(3.66)
потеря кинетической энергии системы при ударе, которая переходит в другие виды энергии, в частности в энергию деформирования и разрушения деталей и элементов конструкций соударяющихся автомобилей.
Вформулах (3.63–3.66) введены следующие обозначения: m1 и m2 – массы соударяющихся автомобилей;
JZ1 |
и |
JZ 2 – |
моменты инерции автомобилей относительно осей, про- |
|
|
|
ходящих перпендикулярно плоскости движения автомо- |
|
|
|
билей через их центры масс; |
|
|
k |
коэффициент восстановления. |
После подстановки выражений (3.64) и (3.66) в (3.63), с учетом (3.65) и соответствующих математических преобразований, получают:
|
(1 k)m1V1U10 cos 1 (1 k)m2V2U20 cos( 2 ) 2T |
где 1 |
и 2 – |
Таким образом, уравнение (3.67) связывает
km V 2 |
km V 2 |
, |
( |
||
1 |
1 |
2 |
2 |
|
|
углы между осью OX и направлениями векторов
скоростей |
U10 |
|
и |
U20 |
(рис. |
3.10).
геометрические (углы
, 1, 2 ) , кинематические (скорости V1, V2 , U10 , U20 ) , энергетические (кине-
тическая энергия Т) и деформационные (коэффициент восстановления k ) параметры удара.
Как правило, при проведении экспертизы геометрические параметры известны, а кинематические требуется определить. Поскольку одного уравнения
68
для этого недостаточно, используют теорему об изменении кинетической энергии при ударе, согласно которой [35]
где
где
Q
и
Q |
|
|
0 |
S |
e |
|
|
–
Q Q |
|
|
|
S |
, |
|
|
|
|
e |
|
(3.68) |
|
|
0 |
|
|
|
количества движения системы в моменты окончания и начала удара соответственно; сумма внешних ударных импульсов. Поскольку внешние (по
отношению к системе «автомобиль 1 – автомобиль 2») им-
пульсы отсутствуют, то S |
e |
0, |
откуда |
|||||||
|
||||||||||
|
|
Q Q |
|
, |
|
|
|
|
(3.69) |
|
|
|
|
0 |
|
|
|
|
|
||
Q m U |
10 |
m U |
20 |
, |
(3.70) |
|||||
|
|
1 |
|
|
2 |
|
||||
Q |
0 |
m V m V . |
(3.71) |
|||||||
|
1 |
1 |
|
|
|
2 |
2 |
|
||
Подстановка двух последних формул в выражение (3.69) дает векторное уравнение сохранения количества движения при ударе:
m U |
10 |
m U |
20 |
m V m V |
, |
|||
1 |
2 |
1 |
1 |
2 |
2 |
|
||
(3.72)
которое широко применяется в автотехнической экспертизе [30, 96]. Проекции этого уравнения на оси координат системы XOY для условий за-
дачи примера 1 (рис. 3.10) имеют вид:
OX:
m U |
10 |
cos |
m U |
20 |
cos |
2 |
m V |
m V cos ; |
||
1 |
1 |
2 |
|
1 |
1 |
2 |
2 |
|||
OY:
m1U10 sin 1 m2U20 sin 2 m2V2 sin .
(3.73)
(3.74)
Вид векторного уравнения (3.72) для всех случаев столкновений сохраняется, то есть остается инвариантным, а его проекции на оси координат (3.73) и (3.74) в каждом конкретном случае столкновения могут иметь свои особенности.
Таким образом, имеем систему из трех уравнений (3.67), (3.73) и (3.74) с пятью неизвестными: V1,V2 ,U10 ,U20 и k .
Из уравнения (3.73) выражают скорость U20 :
U20 |
1 |
(m1V1 |
m2V2 cos m1U10 cos )1. |
(3.75) |
|
|
|||||
m2 cos 2 |
|||||
|
|
|
|
Полученное выражение подставляют в уравнение (3.74), откуда определяют скорость U10 :
69
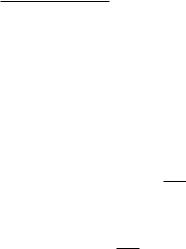
U10 |
|
1 |
|
[m1V1 sin 2 m2V2 sin( 2 )]. |
(3.76) |
|
|
||||
m1 sin( 1 |
|
||||
|
|
2 ) |
|
||
После подстановки (3.76) в (3.75) имеем:
U |
|
|
1 |
|
|
[m V sin |
m V sin( |
)]. |
||||
20 |
|
|
|
|||||||||
|
m sin( |
|
) |
1 |
1 |
1 |
2 |
2 |
1 |
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
1 |
2 |
|
|
|
|
|
|
|
|
(3.77)
Вводятся обозначения:
B1 |
sin 2 |
|
|
|
|
sin( 2 ) |
;C1 |
|
|
sin 1 |
|
|
sin( 1 ) |
||||||||
|
|
; B2 |
|
|
|
|
;C2 |
|
|
. |
|||||||||||
sin( |
) |
sin( |
) |
sin( |
) |
sin( |
) |
||||||||||||||
1 |
2 |
|
|
1 |
|
2 |
|
|
|
|
|
1 |
2 |
|
1 |
2 |
|
|
|||
Тогда формулы (3.76) и (3.77) примут вид: |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
U |
|
B V |
m |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
10 |
|
2 B V , |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
1 |
m |
2 |
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
m |
C V |
C V . |
|
|
|
|
|
|
||||
|
|
|
|
|
|
20 |
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
m |
1 |
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
(3.78)
(3.79)
(3.80)
Полученные формулы подставляют в уравнение (3.67), которое преобразуется в выражение:
m [k (1 k)B cos ]V |
2 |
(1 k)[m C cos( |
|
) m B cos ]V V |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
|
|
1 |
1 |
|
|
2 |
|
|
2 |
2 |
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.81) |
|
|
m [k (1 k)C |
|
cos( |
|
)]V |
2 |
2T. |
|
|
|
|
|
||||||
|
|
2 |
2 |
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
Это уравнение является основным, связывающим скорости автомобилей при соударении V1 и V2 и кинетическую энергию системы T в конце удара. Оно может быть представлено в виде:
2 |
D0V1V2 |
2 |
|
(3.82) |
D1V1 |
D2V2 2T , |
|||
где |
|
|
|
|
D m [k (1 k)B cos ]; |
|
|||
1 |
1 |
1 |
1 |
|
D0 (1 k)[m1C1 cos( 2 |
) m2 B2 cos 1]; |
(3.83) |
||
D2 m2[k (1 k)C2 cos( 2 |
)]. |
|
||
При определении значений D0, D1 и D2 необходимо задаться величиной коэффициента восстановления k. Величина k лежит в интервале от 0 (абсолютно неупругий удар) до 1 (абсолютно упругий удар) [55], в который вписываются все случаи столкновения реальных физических объектов, к каковым относятся автомобили. Однако для конкретных расчетов необходимо задаваться и более конкретными величинами k. Надежной информации по этому поводу нет, что
70