
1556
.pdf
Инвариантность формы полного дифференциала
Теорема. Полный дифференциал функции z f u,v сохраняет
один и тот же вид, независимо от того, являются ли ее аргументы u,v независимыми переменными или функциями от независимых переменных.
dz uz du vz dv.
Указанное свойство справедливо и для функций n независимых переменных.
Свойства дифференциала
Для любых двух функций u и v, имеющих непрерывные частные производные в точке х, справедливы следующие свойства:
1)d u v du dv ;
2)d uv udv vdu ;
3) |
d u |
|
|
vdu udv |
, v 0. |
|
v2 |
||||||
|
v |
|
|
|
Предполагается, что частные производные от функций, стоящих в скобках (слева), непрерывны в точке х.
Дифференцирование неявных функций
Неявная функция одного переменного определяется уравнением F x, y 0 (в общем случае оно может и не определять функцию,
например, уравнение x2 y2 |
5 0 ). |
|
|
Теорема. Если |
F x, y |
непрерывна вместе со своими частными |
|
производными в |
окрестности точки M0 x0 , y0 ; |
F x0 , y0 0 , |
|
Fy x0 , y0 0 , то уравнение F x, y 0 при значениях x, близких к x0 , имеет единственное непрерывно зависящее от x решение y x такое, что x0 y0 .
Функция y x имеет также непрерывную производную.
Если F x, y 0 определяет неявную функцию y x , то должны
иметь:
F x, x 0;
71

|
dF |
F 1 |
F dy 0. |
|
|
|
dx |
x |
y dx |
|
|
|
|
dy Fx . |
|
|
|
|
|
dx |
Fy |
|
|
Здесь dy |
не существует при |
Fy 0 . Но при |
Fy |
0 не гаранC |
|
dx |
|
|
|
|
|
тируется и само существование неявной функции. |
|
|
|||
Пример. |
|
|
|
|
|
|
|
x2 y2 |
1 0. |
|
|
|
|
F x, y x2 y2 1. |
|
|
|
|
|
F 2x, |
F 2y. |
|
|
|
|
x |
y |
|
|
dxdy 22xy xy , y 0 .
Если F x, y, z 0 определяет z как некоторую функцию z x, y ,
то аналогично
z Fx ; z Fy .x Fz y Fz
Геометрические приложения дифференциального исчисления функций двух переменных
Уравнение касательной плоскости в точке M0 x0 , y0 , f x0 , y0 z z0 fx x0 , y0 x x0 fy x0 , y0 y y0 .
Нормальный вектор N fx , fy , 1 .
Уравнение нормали определится как уравнение прямой, проходящей
через точку M0 x0 , y0 , f x0 , y0 и имеющей направляющим вектором a N fx , fy , 1 .
Пусть теперь поверхность задана не в виде z f x, y , а неявно уравнением
F x, y, z 0 .
72

Если выполнены условия теоремы существования неявной функC ции в окрестности точки M0 x0 , y0 , z0 , то определяется неявная
функция z f x, y и
fx x0 , y0 Fx x0 , y0 , z0 ; Fz x0 , y0 , z0
|
|
fy x0 , y0 |
Fy x0 , y0 , z0 |
. |
|
|
||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
Fz x0 , y0 , z0 |
|
|
|
|||
Тогда, |
подставляя значения |
fx x0 , y0 , |
fy x0 , y0 |
|
в приведенные |
|||||||||
выше уравнения, получим: |
|
|
|
|
|
|
|
|
|
|
||||
– уравнение касательной плоскости |
|
|
|
|
|
|
||||||||
|
F |
x x |
|
|
|
F |
y y |
|
|
F |
z z |
|
0. |
|
|
|
|
|
|
|
|
|
|
||||||
|
x 0 |
|
0 |
|
|
y 0 |
|
|
0 |
|
z |
0 |
0 |
|
(индексы “0” обозначают, |
|
что производные вычислены в точке при |
||||||||||||
xx0 , y y0 , z z0 );
–уравнение нормали
x x0 |
|
y y0 |
|
z z0 . |
||||
|
F |
|
|
F |
|
|
F |
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
z 0 |
|||
|
|
y 0 |
|
|||||
Например, напишем уравнения касательной плоскости и нормали в
точке M0 1,1, |
2 для сферы |
x2 y2 |
z2 4 |
z |
R2 x2 y2 : |
||||
|
|
F |
2; |
|
F |
2; |
|
F |
2 2. |
|
|
x 1 |
|
x 1 |
|
x 1 |
|||
|
|
x y 1 |
|
|
y y 1 |
|
|
z y 1 |
|
z 2 |
|
z 2 |
|
|
z 2 |
|||
Откуда: |
|
|
|
|
|
|
||
– уравнение касательной плоскости: |
|
|||||||
2 x 1 y 1 |
2 z |
2 0 , |
||||||
– уравнения нормали: |
|
|
|
|
|
|
||
|
x 1 |
|
y 1 |
|
|
z 2 |
. |
|
|
1 |
|
|
|
||||
|
1 |
|
2 |
|
||||
73

Производная по направлению
Пусть дана гладкая кривая Г
xx t ;
yy t ;
zz t .
( x(t), y(t), z(t) имеют производные в точке t).
Рассмотрим дифференцируемую в точке (x,y,z) функцию трех переменных u u x, y, z . По правилу дифференцирования сложной
функции
u u x t , y t , z t F t
будем иметь:
du u dx u dy u dz . dt x dt y dt z dt
В частном случае, когда параметр t совпадает с длиной дуги s:
|
du |
u dx |
u dy |
u dz . |
|
|
ds |
x ds |
y ds |
z ds |
|
Из ds |
dx2 dy2 |
dz2 |
также следует: |
||
|
dx cos ; |
dy |
cos ; |
dz cos , |
|
|
ds |
|
ds |
|
ds |
где cos , cos , cos – направляющие косинусы направляющего вектора n касательной к кривой Г в точке М.
z |
|
n cos , cos , cos |
|
|
|
|
|

M(x(s),y(s),z(s))
(x0,y0,z0)
y
x
74

Величина |
du |
|
u cos |
u cos |
u cos называется производ3 |
|
ds |
|
x |
y |
z |
ной функции u(x,y,z) вдоль кривой Г или производной по направлению вектора n.
Вектор
|
|
|
|
|
|
|
|
|
|
|
|
u |
, |
u |
, |
u |
|
|
|
|
grad u |
x |
y |
, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|||
называется градиентом функции u(x,y,z). |
|
|
|||||||||||||||
Справедливо |
|
|
|
|
|
|
|
|
|
|
|
|
,n . |
|
|||
|
|
|
|
|
du |
|
|
|
|||||||||
|
|
|
|
|
gradu |
|
|||||||||||
|
|
|
|
|
ds |
|
|||||||||||
|
Экстремум функции нескольких переменных |
||||||||||||||||
Точка P0 x0 , y0 |
называется точкой экстремума (максимума или |
||||||||||||||||
минимума |
функции |
z f x, y , если |
f x0 , y0 есть соответственно |
||||||||||||||
наибольшее или наименьшее значение функции f x, y в окрестности |
|||||||||||||||||
точки P0 x0 , y0 ). |
называется экстремальным значением. |
||||||||||||||||
Значение f x0 , y0 |
|||||||||||||||||
По определению экстремума точка экстремума лежит внутри |
|||||||||||||||||
области определения функции! |
|
|
|
|
|
|
|||||||||||
Необходимый признак экстремума. Если в точке P0 x0 , y0 функция |
|||||||||||||||||
имеет экстремум, то ее частные производные в этой точке равны нулю: |
|||||||||||||||||
|
|
|
|
z |
| |
|
|
0; |
|
z |
| |
0 |
|||||
|
|
|
|
|
|
|
|
|
y |
||||||||
|
|
|
|
x |
yx0 |
|
yx0 |
|
|
||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
||
или не существуют. |
|
z |
|
|
|
z |
|
|
|
|
|
|
|
||||
Точки, |
в которых |
, |
|
обращаются в нуль, называются |
|||||||||||||
|
|
y |
|||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|||||||
стационарными. |
|
|
|
|
|
|
|
|
|
|
Достаточные условия экстремума функции z f x, y |
||||||||||
Пусть A |
2 z |
|
, B |
2 z |
|
|
, C |
2 z |
|
. |
|
|
|
||||||||
x2 |
|
x y |
|
y2 |
|
|||||
|
|
x0 |
x0 |
|
|
x0 |
||||
|
|
|
y0 |
|
|
y0 |
|
|
|
y0 |
Тогда, если P0 x0 , y0 – стационарная точка, то при:
1.B2 AC 0 точка Р0 – точка экстремума:
максимум при A<0, C<0,
минимум при A>0, C>0;
2.B2 AC 0 точка Р0 не является точкой экстремума;
75
3. B2 AC 0 никакого заключения о характере стационарной точC ки сделать нельзя (требуются дополнительные исследования).
Условный экстремум
На линии L, определяемой в плоскости xOy уравнением x, y 0 (уравнение связи), найдем точку P x, y , в которой функция z f x, y
принимает наибольшее или наименьшее значения по сравнению со значениями этой функции в точках линии L, находящихся вблизи точки P. Такие точки называются точками условного экстремума
функции f x, y на линии L.
Для определения точек условного экстремума часто используется метод множителей Лагранжа. Здесь отыскание условного экстремума сводится к исследованию на обычный экстремум так называемой функции Лагранжа x, y f x, y x, y , где – неопределенный
постоянный множитель.
Возможные точки условного экстремума определятся из необходимых условий экстремума функции Лагранжа:
|
|
f |
|
|
0, |
|
|
x |
x |
x |
|||
|
|
|
f |
|
|
|
|
|
|
0, |
|||
|
y |
y |
y |
|||
x, y 0. |
|
|
||||
|
|
|
|
|
|
|
(достаточные условия не приводятся).
Задачи о наибольших и наименьших значениях функции
Для того чтобы найти наибольшее и наименьшее значения функции z f x, y в замкнутой области, нужно найти все максимумы или
минимумы функции, достигаемые внутри этой области, а также наибольшее или наименьшее значения функции на границе области (наибольшее из всех этих чисел и будет искомым наибольшим значеC нием, а наименьшее – наименьшим).
Метод наименьших квадратов
Метод наименьших квадратов (МНК) состоит в выборе функции
|
|
|
|
|
n |
i |
|
|
|
i |
|
i |
|
i |
|
y |
x |
из условия минимума I |
|
|
x |
, y |
, где |
||||||||
|
|
y |
|
|
2 по точкам |
|
x |
|
|||||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
yi – полученные экспериментально значения y в точке xi .
76
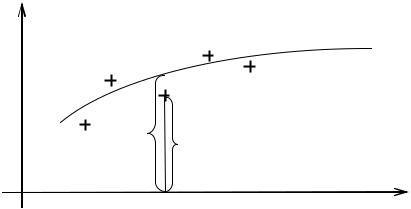
y
y= (x)
 (xn,yn)
(xn,yn)
(xi) yi
x
Если по результатам наблюдений определяются наиболее вероятC ные значения коэффициентов полинома
y a0 a1x a2 x2 am xm y x ,
a0 ,a1,a2, ,am находятся из условия
n |
|
|
yi a0 a1xi a2 xi2 am xim |
2 min , |
|
i 1 |
|
|
то есть из условий минимума функции многих переменных |
||
n |
|
2 , |
a0 , ,am yi a0 a1xi a2 xi2 am xim |
||
i 1 |
|
|
зависящей от a0 ,a1,a2, ,am ( xi , yi – известные числа).
Для определения стационарных точек этой функции следует приравнять частные производные относительно a0 ,a1,a2, ,am нулю:
|
n |
|
2 |
m |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
a0 |
2 |
yi |
a0 a1xi a2 xi |
am xi |
|
1 0; |
|
||||
|
i 1 |
|
|
|
|
|
|
|
||||
|
|
n |
|
a0 a1xi a2 xi2 am xim |
|
|
||||||
|
|
|
|
2 |
yi |
xi 0; |
|
|||||
a1 |
|
|||||||||||
|
i 1 |
|
|
|
|
|
|
|
||||
|
|
n |
|
2 |
m |
|
|
2 |
|
|||
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
yi |
a0 a1xi a2 xi |
am xi |
|
xi 0; |
|
||
a2 |
||||||||||||
|
i 1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
n |
|
|
|
|
|
|
|
|||
|
|
2 |
m |
|
m |
|
||||||
|
|
|
|
2 yi |
a0 a1xi a2 xi |
am xi |
|
xi 0. |
|
|||
am |
|
|
||||||||||
|
i 1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
77 |
|
|
|
|
|
|

Откуда
|
|
n |
n |
n |
n |
|
a0n a1 xi a2 |
xi2 am xim |
yi ; |
|
|||
|
|
i 1 |
i 1 |
i 1 |
i 1 |
|
|
n |
n |
n |
n |
n |
|
a0 |
xi a1 xi2 a2 xi3 am xim yi xi ; |
|||||
|
i 1 |
i 1 |
i 1 |
i 1 |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
n |
|
n |
n |
a0 |
xim a1 xim 1 a2 xim 2 am xi2m yi xim . |
|||||
|
i 1 |
i 1 |
i 1 |
|
i 1 |
i 1 |
В частном случае при сглаживании полиномом |
|
|||||
|
|
|
y ax b |
|
|
|
(здесь a0 b, a1 |
a, m 1) а0, а1 определятся из системы уравнений |
|||||
|
|
|
n |
n |
|
|
|
|
a0n a1 xi |
yi |
|
|
|
|
|
|
i 1 |
i 1 |
|
|
|
|
n |
n |
n |
|
|
|
|
a0 xi a1 xi2 yi xi . |
|
|
||
|
|
i 1 |
i 1 |
i 1 |
|
|
ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Комплексным числом z называется упорядоченная пара чисел x, y , x Re z – действительная, y Im z – мнимая части. Запись числа z в виде z x iy называется алгебраической формой комплексного числа. Символ i называется мнимой единицей ( i2 1).
Если x 0 , |
то число |
0 iy iy называется чисто мнимым, если |
y 0 , то число |
x i 0 x |
отождествляется с действительным числом |
x . Множество R действительных чисел является подмножеством множества C всех комплексных чисел ( R C ).
Два комплексных числа z1 x1 iy1 и z2 x2 iy2 называются равC
ными тогда и только тогда, когда равны их действительные и мнимые части, то есть z1 z2 при x1 x2 и y1 y2 . В частности, комплексное
число z x iy равно нулю тогда и только тогда, когда x y 0 .
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Два комплексных числа z x iy и z x iy , отличающиеся тольC ко знаком мнимой части называются сопряженными.
78

Всякое комплексное |
число z x iy можно изобразить точкой |
M x, y плоскости xOy . |
Плоскость, на которой изображаются комC |
плексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной осью, а ось ординат – мнимой.
Комплексное число z x iy можно |
изобразить и с помощью |
||||||||||||||||||
радиусCвектора |
|
|
|
|
|
|
|
x, y . |
|
|
|||||||||
|
OM |
|
|
||||||||||||||||
r |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
x |
|
|
Длина вектора |
|
называется модулем |
|
комплексного числа z, обоC |
|||||||||||||||
|
|
||||||||||||||||||
r |
|||||||||||||||||||
значается |
|
z |
|
или r ; r |
|
z |
|
|
x2 y2 . |
|
|
||||||||
|
|
|
|
|
|
||||||||||||||
Величина угла между положительным направлением действительC
ной оси и вектором |
|
, изображающим комплексное число, |
называется |
r |
|||
аргументом этого числа, обозначается Arg z или . |
Аргумент |
||
комплексного числа z 0 не определен. Аргумент комплексного числа
z 0 – величина многозначная |
и определяется с точностью до |
||||||||||
слагаемого 2 k : |
Arg z arg z 2 k , |
где arg z |
– главное значение аргу3 |
||||||||
мента, заключенное в промежутке , . |
|
|
|
|
|
|
|
||||
Запись числа z в виде z r cos i sin |
называется тригономет3 |
||||||||||
рической формой комплексного числа. |
|
|
|
|
|
|
|
||||
Аргумент определяется из |
формул cos |
x |
, sin |
y |
, tg |
y |
. |
||||
r |
r |
|
|||||||||
|
|
|
|
|
|
|
x |
||||
Иногда в качестве главного значения аргумента берут величину, приC |
|||||||||||
надлежащую промежутку 0,2 , тогда |
|
|
|
|
|
|
|
||||
|
y |
, при x 0, y 0 (для внутренних точек I четв.); |
|||||||||
arctg |
|
||||||||||
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
y |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
arg z arctg |
|
2 , при x 0, y |
0 (для внутренних точек IV четв.); |
||||||||
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
y |
, при x 0 (для внутренних точек II,Ш четв.). |
|||||||||
arctg |
|
||||||||||
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
79
Используя формулу Эйлера ei cos i sin , комплексное число z можно записать и, в так называемой, показательной (или экспоненC
циальной) форме: z r i , где r |
|
z |
|
– |
модуль комплексного числа, а |
|
|
||||
угол Arg z arg z 2 k . |
|
||||
Суммой двух комплексных чисел |
z1 x1 iy1 и z2 x2 iy2 назыC |
||||
вается число, определяемое равенством |
|
||||
x1 iy1 x2 iy2 x1 x2 i y1 y2 .
Вычитание определяется как действие, обратное сложению:
x1 iy1 x2 iy2 x1 x2 i y1 y2 .
Произведением комплексных чисел z1 x1 iy1 и z2 x2 iy2 назыC вается комплексное число, определяемое равенством:
x1 iy1 x2 iy2 x1x2 y1y2 i x1y2 y1x2 . Получается путем перемножения двучленов x1 iy1 и x2 iy2 с
учетом i2 1:
x1 iy1 x2 iy2 x1x2 iy1x2 iy2x1 i2y1y2 x1x2 y1y2 i x1y2 y1x2 .
Частное двух комплексных чисел находят путем умножения числиC теля и знаменателя на число, сопряженное знаменателю (избавляются от мнимости в знаменателе):
|
x iy |
|
x1 iy1 x2 |
iy2 |
|
x x |
2 |
y y |
y x |
2 |
x y |
|
|
0 . |
|||||
|
1 1 |
|
|
|
|
|
1 |
|
1 1 |
i |
1 |
1 2 |
, п р и |
z |
|
||||
|
|
x2 iy2 x2 iy2 |
|
|
|
|
|
|
|
2 |
|||||||||
|
x2 iy2 |
|
|
x22 y22 |
x22 y22 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
При |
|
умножении |
комплексных |
чисел z1 r1 cos 1 i sin 1 |
и |
|||||||||||||
z2 r2 cos 2 i sin 2 , |
заданных в |
|
тригонометрической форме |
их |
|||||||||||||||
модули перемножаются, а аргументы складываются, то есть z1 z2 r1 cos 1 i sin 1 r2 cos 2 i sin 2
= r1 r2 cos 1 2 i sin 1 2 .
Откуда следует формула Муавра для возведения комплексных чисел в натуральную степень:
zn r cos i sin n r n cos n i sin n .
80
