
1556
.pdf
Примером точки разрыва первого рода (рис.8) является точка x = –1 для функции
x 2, |
если |
x 1; |
|
если |
1 x 1; |
f x x 2 1, |
||
|
если |
x 1. |
x 3, |
Односторонние пределы: |
|
|
|
|||||
|
|
|
lim |
f x lim |
x 2 1 2 1; |
|
||
|
|
|
x 1 0 |
|
x 1 0 |
|
|
|
|
|
|
x 1 |
|
|
x 2 1 1 1 2 ; |
|
|
|
|
|
lim |
|
f x lim |
|
||
|
|
|
x 1 0 |
x 1 0 |
|
|
||
|
|
|
x 1 |
|
|
|
|
|
lim |
f x |
lim |
f x |
функция f x в точке x = –1 терпит конечный |
||||
x 1 0 |
x 1 0 |
|
|
|
f x lim |
f x 2 1 1 . |
||
разрыв; скачок функции в этой точке lim |
||||||||
|
|
|
|
|
|
x 1 0 |
x 1 0 |
|
И з |
lim f x |
lim |
f x 2 следует, что функция |
f x в точке |
||||
|
x 1 0 |
|
x 1 0 |
|
|
|
|
|
x = 1 непрерывна.
y
|
2 |
|
|
1 |
x |
|
|
|
1 0 |
1 |
3 |
Рис.8
ДИФФЕРЕНЦИАЛЬНЫЕ ИСЧИСЛЕНИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Производная функции
Определение. Производной функции y= f(x) называется предел отношения приращения функции к приращению аргумента при
произвольном стремлении этого приращения к нулю: |
||||
lim |
f x x f x |
|
||
x |
|
, |
||
x 0 |
||||
|
|
|||
51
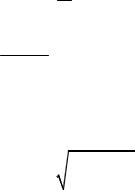
обозначается |
f (x). |
Значение производной функции f (x) в точке х0 |
|||
обозначается |
f (x0) |
или y |
|
x x0 |
(подставляя в f (x) значение x0 |
|
|||||
|
|
||||
определяется f (x0)).
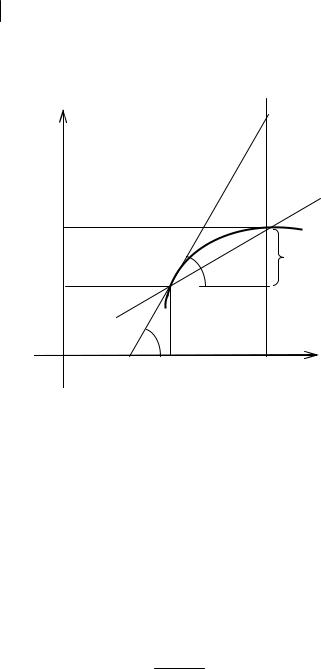
Геометрический смысл производной
Теорема. Если значение производной от функции y= f(x) при х=х0
равно f x0 y x x0 , то прямая, проведенная через точку М0(х0,y0) с угC
ловым коэффициентом, равным f (x0), является касательной к графику функции в точке М0.
y |
T |
|
|
|
M |
|
y0+ y |
|
|
B |
|
|
M0 |
|
y |
|
y0 |
R |
|||
A |
|
|||
|
x |
|||
|
|
|
|
|
|
|
|
x |
|
|
x0 |
|
x0+ x |
|
Касательная и нормаль к линии
Уравнение касательной к линии в точке M0(x0,y0) определяется как уравнение прямой, проходящей через точку M0(x0,y0) с угловым коэффициентом, равным f (x0):
y y0 f x0 x x0 .
Уравнение нормали определяется как уравнение прямой, проC ходящей через точку M0(x0,y0) перпендикулярно касательной:
y y0 f 1x0 x x0 .
52

Основные правила дифференцирования
Предполагается, что слагаемые, сомножители, делимое, делитель непрерывны и имеют производные при рассматриваемых значениях независимой переменной.
1)с = 0;
2)х = 1 ;
3)(u v)= u v ;
4)(cu) = cu ;
5)(uv) = u v + uv ;
6)u u v 2uv ; v v
7)если y=f(u), u=u(x), то есть, если y=f[u(x)], где f(u) и u(x) имеют
производные, то
yx yuux ,
8) если y=f(х) и х= (y) взаимно обратные функции, то
y f 1x .
Формулы для дифференцирования основных функций
1) |
un n un 1 u ; |
|
9) cosu |
sin u u ; |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
u |
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|||||||||
2) |
|
|
|
|
|
|
|
; |
|
10) |
tgu |
|
|
|
|
; |
|
|
|
|
|
|
|||||||
2 u |
|
cos2 u |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
cu |
|
|
|
|
|
u |
|
|
|
|
||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
3) |
|
|
|
|
|
|
; |
|
|
11) |
ctgu |
|
|
|
|
; |
|
|
|
|
|
||||||||
u |
u2 |
|
|
sin2 u |
|
|
|
|
|||||||||||||||||||||
|
eu euu ; |
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|||||||||||||
4) |
|
|
12) |
arctgu |
|
|
|
; |
|
|
|||||||||||||||||||
|
|
|
1 u2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5) |
au au ln a u ; |
13) |
arctgu |
|
|
|
; |
|
|
||||||||||||||||||||
|
1 u2 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|||||
6) |
ln u |
|
|
; |
|
|
14) |
arcsin u |
|
|
|
; |
|||||||||||||||||
u |
|
|
|
1 u2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
||||||||||
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
7) |
loga u |
|
|
; |
15) |
arccosu |
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||
u |
ln a |
|
|
1 u2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
8) sin u cosu u ;
53

Для нахождения производных степенноCпоказательных и некотоC рых других функций применяется логарифмическое дифферен3
цирование (состоит в нахождении логарифмической производной
ln f x ff xx ).
Так, из y x x следует
ln y x ln x. Дифференцируя по x обе части. получим
1y yx x ln x x ln x
|
|
|
|
|
|
y |
1 ln x x |
1 |
|
|
|
|
|
|
|
y |
x |
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
y y ln x 1 . |
|||
|
x x |
|
|
|
|
|
|||
Откуда |
|
x x |
|
ln x 1 . |
|
|
|||
Производные неявных функций
Если y задана уравнением, связывающим независимую переменную х с функцией y, не разрешенным относительно y, то производную от этой функции можно найти, дифференцируя по х обе части уравнения, с учетом того, что y есть функция от х, определяемая этим уравнением.
Например, для неявно заданной функции y2 x ln xy имеем
2yy 1 |
1 |
|
y x y |
; |
y x |
|
x2 |
||
|
|
|
2xy2 y xy y x y .
Разрешая относительно y , получим
y |
xy y |
. |
|
||
|
2xy2 x |
|
54

Дифференцирование параметрически заданных функций
Если х= (t); y= (t), то
yx tt .
Дифференциал
Если f x lim |
y |
есть определенное число, то |
y |
отличается от |
x 0 |
x |
|
x |
|
f (x) на бесконечно малую:
y f x ,x
y f x x x
( 0 при х 0).
Первое слагаемое f (x) х – главная часть приращения, линейная относительно х (при f (x) 0); называется дифференциалом функции и обозначается dy или df(x).
Для функции y= x имеем:
yx x 1 dy dx 1 x.
Таким образом, дифференциал dx независимого переменного x совпадает с его приращением х.
Поэтому
dy f x dx .
Имеем f x dxdy (производную f (x) можно рассматривать как
отношение дифференциала функции к дифференциалу независимого переменного).
Из
f x x f x f x dx
следует
f x x f x f x x, |
|
Что позволяет вычислить f x x по f(x), |
f (x), dx (ошибка |
вычисления равна x ). |
|
55

Геометрический смысл дифференциала
y
T
y+dy
M1
y+ y
dy
|
|
|
y |
y |
M |
|
|
|
|
R |
|
|
|
|
x |
|
x |
|
x+dx |
RT f x dx dy, M1T y dy; |
M1T 0 |
при dx 0 и является бескоC |
|
нечно малой более высокого порядка, чем отрезок MR.
Свойства дифференциала
1.d u v w du dv dw .
2.d uv vdu udv ; d(cu) = cdu.
3. |
u |
|
vdu udv |
,v 0 . |
|||
d |
|
|
|
|
|||
|
v |
2 |
|||||
|
v |
|
|
|
|||
4. |
Если |
y=f(x), |
u= (x) – непрерывные функции, имеющие |
||||
производные f u и x, то y fu x dxdy dudy dxdu ; правая часть равенства
получается из левой просто умножением и делением на du (du 0). Выражение для дифференциала функции y=f(и) сохраняет свой вид, независимо от того, является ли ее аргумент и независимой переменной или функцией от независимой переменной (свойство инвариант3 ности).
5. Непосредственно из п.4 следует правило дифференцирования обратной функции:
y |
|
dy |
|
|
1 |
|
|
1 |
. |
|
|
|
|
|
|||||
x |
|
dx |
dx |
|
|
xy |
|||
|
|
|
|
||||||
|
|
|
|
|
dy |
||||
|
|
|
|
|
|
|
|
|
|
56
Дифференцируемость функции
Определение. Функция y=f(x) называется дифференцируемой в точке х, если y A x 0 x .
Геометрически дифференцируемости функции соответствует сущеC ствование у линии y=f(x) касательной, не перпендикулярной к оси ОХ.
Из дифференцируемости f(x) следует ее непрерывность:
lim y f x y f x x
x 0 x
и у 0 при х 0, y=f(x) непрерывна в точке х.
Обратное не всегда верно.
Производные и дифференциалы высших порядков
Пусть y=f(x) имеет производную f (х) в некотором интервале незаC висимой переменной х. Тогда производная от f (х) называется проC изводной второго порядка или второй производной функции f(x):
|
f x lim |
f x x f x |
. |
|
|
|
|
|
|
||||
|
x 0 |
x |
|
|||
Производной nCго порядка |
f h x называется |
производная от |
||||
производной (n–1)Cго порядка: |
|
|
|
|
||
f |
n x lim |
f n 1 x x f n 1 x |
|
, |
||
|
||||||
|
x 0 |
x |
|
|||
в частности, производная второго порядка или вторая производная функции f(x):
f x lim |
f x x f x |
. |
|
||
x 0 |
x |
|
Функция f (x) в точке x определяет скорость изменения f (x), то есть f (x) – ускорение изменения функции f(x) при данном х.
Производные f x в данной точке могут существовать до опC
ределенного порядка, а производных высшего порядка функция в этой точке может и не иметь.
Однако всякая элементарная функция, за исключением, быть моC жет, отдельных точек, имеет в своей области определения производные любых порядков.
57
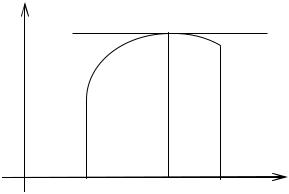
Например, для y xn :
y nxn 1,
y n n 1 xn 2,
…
y n n!,
y n 1 y n 2 0.
Производные неявных функций
Для отыскания высшей производной неявных функций надо соответствующее число раз продифференцировать заданное уравнение, связывающее х и у, помня, что у и все ее производные есть функции х.
Например,
x2 y2 1.
2x 2yy 0 x yy 0, y xy ;
1 y y yy 0 y 1 y 2 y
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
y |
2 |
x |
2 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y |
|
|
y |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
y |
|
|
|
|
y3 |
|
y3 |
|
x |
2 |
|
3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Производные параметрически заданных функций
Из х= (t), y=f(t) следует:
|
|
|
y |
dy |
|
|
f t |
; |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
dx |
|
|
|
t |
|
|
|
|
|||||||||
|
|
|
f t |
|
|
|
|
|
|
|
f t |
|
|
||||||||
|
|
d |
|
|
|
|
d |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
t |
|
|
|
|
|
|
|
t |
|
|
||||||||
|
y |
|
|
|
|
|
|
|
dt |
|
|||||||||||
|
|
dx |
|
|
|
|
|
|
|
dt |
|
|
dx |
||||||||
|
f t t t f t |
|
|
|
1 |
|
|
|
|
f t |
t t f t |
||||||||||
t 2 |
|
|
|
|
t |
|
|
|
|
|
t 3 |
||||||||||
… .
58
Например, если |
x a cost , |
y bsin t , то |
y x |
bcost |
|
b |
|||||||||
|
|
ctg t ; |
|||||||||||||
a sin t |
a |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
ctg t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y x |
y x t |
|
|
|
a |
t |
|
b |
. |
|
|
|
|
|
|
|
|
a sin t |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
a2 sin3 t |
|
|
|
|
|
|||||
|
a cost t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференциалы высших порядков
Определение. Дифференциалом nCго порядка dny называется диффеC ренциал от дифференциала (nC1)Cго порядка как функции х:
d n y = d ( d n C 1 y ) .
В частности,
d 2 y d dy dy dx.
Замечая, что dx от х не зависит, получим:
d 2 y f x dx dx f x dx dx f x dx2.
Аналогично
d n y f n x dxn .
Применение дифференциального исчисления к исследованию функций
Приведем несколько широко используемых теорем.
Теорема Ферма. Если y=f(x), непрерывная в интервале [х1, х2], принимает свое наибольшее (или наименьшее) значение во внутренней точке этого интервала (х1< <х2), то есть, если в точке существует функция f(x), то обязательно производная f 0 или не существует.
Геометрический смысл теоремы Ферма
y
М
x1 |
|
x2 |
x |
Касательная к графику функции в его наивысшей (наинизшей) точке параллельна оси абсцисс или не существует.
59

Теорема Ролля. Если функция y=f(x): непрерывна в замкнутом интервале [х1, х2], дифференцируема во всех его внутренних точках; имеет на концах интервала равные значения, то в интервале [х1, х2] существует хотя бы одно значение х= , для которого f ( )=0.
Геометрический смысл теоремы Ролля
На линии y=f(x), где f(x) удовлетворяет условиям теоремы Ролля, найдется точка, в которой касательная параллельна оси абсцисс.
y
М
f(x1)= f(x2)
x1 x2 x
Теорема Лагранжа (о конечных приращениях).
Если функция f(x): непрерывна в замкнутом интервале [х1,х2], дифференцируема во всех его внутренних точках, то в этом интервале существует хотя бы одно значение х= , для которого
fx2 f x1 f . x2 x1
Геометрический смысл теоремы Лагранжа
Теорема утверждает, что если во всех точках дуги АВ существует касательная, то на этой дуге найдется точка С между А и В, в которой касательная параллельна хорде АВ.
|
f x2 f x1 |
tg f . |
|
y |
x2 x1 |
||
|
|||
|
|
||
|
C |
B |
f(x2)–f(x1)
A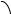
|
|
x2–x1 |
|
|
x1 |
x2 |
x |
60
