
1556
.pdfЕ – область задания f(x);
Е1 – область значений f(x) (образ множества Е). Пусть
Е1 = f ( Е ) ;
Е2 = F ( Е 1 ) .
Имеем
Е 2 = F ( f ( Е ) ) .
Функция z=F(f(x)), z Е2, y Е1, x Е называется сложной функцией
или суперпозицией f и F.
Если в образовании сложной функции участвует n функций, то
z = F 1 ( F 2 ( F 3 ( … ( F n ( x ) … ) ) ) ) .
Пример.
z atg x2 1. Здесь z au 1, w au, u tg v, v x2;
z=F1(F2(F3 ((F4(x))))); v F4 x x2; u F3 x tg v; w F2 u au; z F1 w w 1.
Способы задания функций
1.Аналитически (формулой)
2.Графически
3.Таблично
4.Программой для ЭВМ.
Функция называется четной, если f(–x)= f(x) и нечетной, если f(–x)= –f(x).
Произведение четной функции на нечетную есть нечетная функция. Произведение двух четных или нечетных функций есть четная
функция.
Если f(x+T)=f(x) (T 0 ) x из ОДЗ, то функция называется
периодической.
Если каждому x E поставлено в соответствие множество нескольC ких чисел y, то говорят, что определена многозначная функция у= f(x).
Функция одной переменной может быть задана неявно уравнением F(x,y)=0.Переход к явному заданию функции от неявного не всегда возможен.
41
Если y= f(x) осуществляет взаимно однозначное отображение |
Е в |
E1, то и каждому у Е1 ставится в соответствие единственное |
x Е |
(определяется функция y= (x)). Функции y= f(x) и y= (x) называютC ся взаимно обратными.
Способы определения взаимно обратных функций.
1. Если y= f(x), то уравнение y – f(x)= 0 определяет х как неявную функцию от у. Чтобы получить ее явное выражение, надо (если возможно) разрешить это уравнение относительно х, то есть предстаC вить в виде y = (x). Функции y = f(x), y = (x) будут взаимно обратC ными. Например:
y10x; y 10x 0 10x y; x lg y.
2.Если функция сразу задана в неявном виде, то, разрешая это
уравнение сначала относительно y, затем – x, найдем взаимно обратC ные функции y = f(x), y = (x). Например:
x2y 1 0.
y 1 x
2
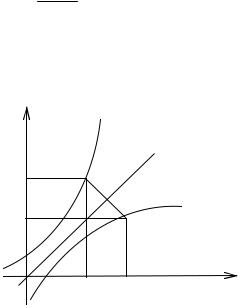
Графики функций y = f(x), относительно прямой y = x.
; x 2y 1 .
y = (x) расположены симметрично
y |
y= (x) |
|
|
M (b,a) |
y= x |
|
|
|
(b)=a |
|
y= f(x) |
|
|
|
f(a) |
M(a,b) |
|
0 |
f(a) a = (b) |
x |
Функция y = f(x) называется возрастающей в интервале, если большим значениям x соответствуют бульшие значения y. Аналогично определяется убывающая функция.
Интервалы возрастания и убывания функции называются интерC валами монотонности функции.
42
Значение функции, большее (меньшее) всех других ее значений в |
||||
некотором интервале, называется наибольшим (наименьшим) |
||||
значением функции в этом интервале. |
|
|||
|
|
Предел функции |
|
|
Число А называется пределом f(x) в точке х0, если она определена |
||||
в некоторой окрестности точки х0, за исключением, быть может, самой |
||||
точки х0, и если для всякого >0 найдется такая 0 , что для |
||||
всех |
|
|
|
|
|
|
|
x x0 |
|
имеет место: |
|
f x A . |
|
|
|
|
|
||
Обозначают |
|
lim f x A, |
|
|
|
|
x x0 |
|
|
или |
|
f x A(x x0 ). |
|
|
y |
|
|
|
|
|
|
|
|
y =A+ |
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y =f(x) |
|
|
y =A– |
|
|
|
|
|
0 |
|
x0– |
x0 x0+ |
x |
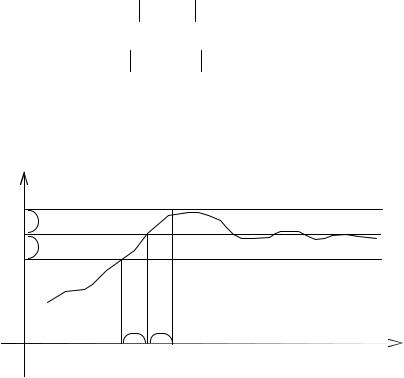
Для всех точек, лежащих в Cинтервале, график y= f(x) |
лежит |
внутри полосы шириной 2 . |
|
Заметим, что для существования lim f x не требуется, |
чтобы |
x x0 |
|
функция была определена в самой точке х0.
Число A1 (A2) называется пределом функции f(x) в точке х0 слева (справа), если f(x) A1(A2) при х х0, и при этом х принимает лишь значения, меньшие (большие) х0.
Можно доказать, что если существуют А1 и А2, где А1 = А2=А, то
lim f x A.
x x0
И обратно: если существует
lim f x A ,
x x0
43
то существуют пределы слева и справа, при этом
lim f x A,
x x0 0
lim f x A.
x x0 0
Предел функции в бесконечности
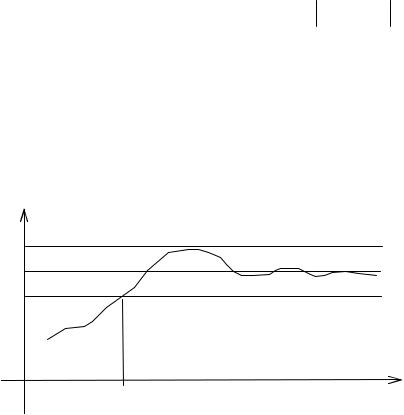
Число А называется пределом y= f(x) при x , если для всех достаточно больших значений х соответствующие значения f(x) как угодно мало отличаются от А ( 0, x0 0 : x x0 f x A ).
Пишут
lim f x A
x
или
f ( x ) А ( x ) .
Аналогично определяется lim f x .
x
f(x)
A+
А
A–
0 |
x0 |
x |
При x (х х0) график y= f(x) будет находиться в полосе, ограC |
||
ниченной прямыми |
y=A – ; y=A + . |
|
Ограниченность функции, имеющей предел |
||
Теорема. Если |
lim f x A , где |
А – конечное число, то на |
|
x x0 |
|
некоторой окрестности u(x0) точки x0 функция f(x) ограничена, то есть |
||||||
существует такое М >0, что |
|
f x |
|
M x u x0 |
, |
x x0 . |
|
|
|||||
. |
|
|
|
|
|
|
|
Переход к пределу в неравенствах |
Если lim f1 x A1 , |
|
x x0 |
x A2 |
lim f2 |
|
x x0 |
|
44

и на некоторой окрестности u(x0), x x0 имеет место f1 x f2 x ,
то A1 A2.
Если lim f1 x |
lim f2 x A |
x x0 |
x x0 |
и на некоторой окрестности u(x0), x x0 |
|
|
f1 x x f2 x , |
то |
lim x A. |
|
|
|
x x0 |
Бесконечно большие величины
Определение. Функция y=f(x) называется бесконечно большой величиной при x x0, если для всех значений x, достаточно мало отличающихся от x0, соответствующие значения f(x) по абсолютной величине превосходят любое наперед заданное сколь угодно большое
положительное число. |
lim f x . |
Пишут: |
|
|
x x0 |
Иначе говоря, какое бы большое число М не взяли, найдется такое>0, что при x x0 будем иметь f x M .
Не смешивать бесконечно большое число с большим постоянным числом!
Бесконечно малые величины
Определение. Функция у = f(x), стремящаяся к нулю при x x0, называется бесконечно малой величиной при x x0. Например:
y=x2 при x 0, y 0; y=x–1 при x 1, y 0.
Не смешивать постоянное очень малое число с бесконечно малой величиной! Единственным числом, которое рассматривается в качестве бесконечно малой величины, служит нуль (и то лишь потому, что предел постоянной величины равен ей самой).
Теорема. Если функция f(x) – бесконечно большая величина, то
1
f x – бесконечно малая величина.
Если (x) 0 – бесконечно малая величина, то |
1 |
|
– бесконечно |
|
|
||
x |
|||
большая величина. |
|
|
|
45

Теорема (прямая). Если функция имеет предел, то ее можно представить как сумму постоянной, равной ее пределу, и бесконечно малой величины, то есть
f(x) = А+ (х).
Теорема (обратная). Если функцию можно представить как сумму постоянной и бесконечно малой величины, то постоянное слагаемое
есть предел функции, то есть из f(x) = А+ (х), следует lim x 0.
x x0
Правила предельного перехода
Теорема. Сумма конечного числа бесконечно малых величин есть бесконечно малая величина.
Следствия:
1. Предел суммы конечного числа слагаемых равен сумме пределов этих слагаемых, если существуют пределы слагаемых.
2. Произведение ограниченной функции на бесконечно малую величину есть бесконечно малая величина.
3. Предел произведения конечного числа множителей равен произведению пределов этих множителей, если существуют пределы сомножителей.
4. Частное от деления бесконечно малой величины на функцию u, предел которой отличен от нуля, есть бесконечно малая величина.
4 . Предел частного равен частному от деления пределов, если существуют пределы числителя и знаменателя, и предел знаменателя
не равен нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1. |
|
|
lim 3x 5 |
|
lim 3x lim 5 |
|
||||||
|
3x 5 |
|
|
|||||||||
lim |
x 1 |
|
|
|
|
x 1 |
|
x 1 |
|
|||
lim 4x |
2 |
lim 4x lim 2 |
||||||||||
x 1 |
4x 2 |
|
|
|||||||||
|
|
|
x 1 |
|
|
|
|
x 1 |
|
x 1 |
|
|
|
|
3 lim x 5 |
|
3 1 |
5 |
8 |
|
|
||||
|
|
x 1 |
|
|
4. |
|
||||||
|
4 lim x 2 |
|
|
2 |
|
|||||||
|
|
|
4 1 2 |
|
|
|||||||
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
Пример 2. Найти
lim x2 4 .
x 2 x 2
0 Имеем неопределенность вида 0 :
x2 4 |
|
x 2 x 2 |
x 2. |
|
x 2 |
x 2 |
|||
|
|
46
Указанное преобразование справедливо при всех х 2. Поэтому, по определению предела, где в самой точке х0 функция может быть и не определена, будем иметь:
|
|
|
|
lim x2 4 lim x 2 4. |
|
|
|
|
||||||||
|
|
|
|
x 2 x 2 |
x 2 |
|
|
|
|
|
|
|||||
|
|
|
|
Неопределенности вида |
, 0. , |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нельзя определить пределы при x x0 без специальных исC |
|||||||||||||||
следований, |
если: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
– |
и v и требуется найти lim |
u |
|
|
|
|
|
||||||||
|
v |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
||||
|
– |
и 0 v и требуется найти lim uv ; |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
||
|
– |
и v и требуется найти lim (u v). |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
||
|
Если предел числителя и не равен нулю, а предел знаменателя v |
|||||||||||||||
равен |
|
нулю, |
то величина |
v |
бесконечно малая |
(так |
как |
lim u 0 , |
||||||||
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
x x0 |
|
lim v 0 ). Тогда предел |
обратной |
величины |
есть |
и |
u |
есть |
||||||||||
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
бесконечно большая величина. |
|
|
|
|
|
|
|
|
|
|||||||
|
Пример 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Найти |
|
lim |
|
1 |
|
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|||||||
|
При х 1 |
|
x |
1 x |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
х – 1 0 , |
|
|
|
|
|
|
||||
а числитель 1. |
lim x 1 |
|
|
|
|
|
|
|
||||||||
Так что |
|
0 |
0 , |
|
|
|
|
|||||||||
|
1 |
|
|
|
x 1 |
1 |
|
|
1 |
|
|
|
|
|
|
|
и |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример 4. Найти lim x 1. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x x 1 |
|
|
|
|
|
|
|
|
|
|||
|
Это неопределенность вида |
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
47
Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
x |
|
|
1 |
|
1 lim |
|
1 |
|
|
1 0 |
|
||||||||
|
|
|
|
x |
x |
|
|
|
|
|
|
||||||||||||||
lim |
|
lim |
|
|
|
|
|
|
|
x x |
|
1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x x 1 |
x x |
|
|
|
1 |
1 |
lim |
1 |
|
|
1 0 |
||||||||||||||
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x x |
|
|
|
|
||||||||
(так как х – бесконечно большая величина, то |
1 |
– бесконечно малая |
|||||||||||||||||||||||
|
x |
||||||||||||||||||||||||
величина). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0 xm a1xm 1 am |
|
0, если |
m n; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Пример 5. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, если |
m n; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x b0 xn b1xn 1 bn |
|
a |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
, если m n. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
Теорема. Если значения функции f(x) заключены между соответC ствующими значениями функций F(x) и (x), стремящихся при х х0 к одному и тому же пределу А, то f(x) при х х0 имеет предел, также равный А.
Замечательные пределы
Используя теорему легко получить важное предельное соотноC шение (первый замечательный предел).
lim sin x 1. |
||||
x 0 |
x |
|
||
Так же широко используется при определении пределов функций и |
||||
второй замечательный предел |
|
|
|
|
|
|
1 |
x |
|
lim 1 |
|
|
e . |
|
x |
||||
x |
|
|
||
Сравнение бесконечно малых величин
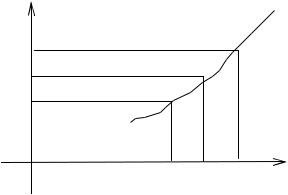
Для того чтобы сравнить между собой две бесконечно малые велиC
чины x и x , берут предел их отношения |
|
(х х0 или х ). |
|
|
|
Определение. Если отношение имеет конечный предел lim A 0
48
|
|
|
1 |
0 |
|
|
lim |
|
|
, |
|||
A |
||||||
|
|
|
|
то бесконечно малые величины и называются бесконечно малыми
одного порядка.
Определение. Если и – бесконечно малые величины одного порядка и
lim 1,
то и называют эквивалентными или равносильными бесконечно малыми и пишут ~ . (Здесь lim 1).
Предел отношения бесконечно малых не изменится, если их заменить эквивалентными бесконечно малыми.
З а м е ч а н и е . Если отношение двух бесконечно малых величин не имеет предела и не стремится к , то и не сравнимы между собой в указанном выше смысле.
Непрерывные функции
Определение. Приращением функции y=f(x) в данной точке х0 называется
y = f ( х0 + x ) – f (х0), где x – приращение аргумента.
y
y= f(х)
y f(х0) y
x x
x
x0
Определение. Функция y=f(x) называется непрерывной в точке х0,
если lim f x f x0 .
x x0
Эквивалентное этому другое определение: функция y=f(x) назыC вается непрерывной в точке х0, если она определена в некоторой
окрестности точки x0 и если lim y 0 .
x 0
49
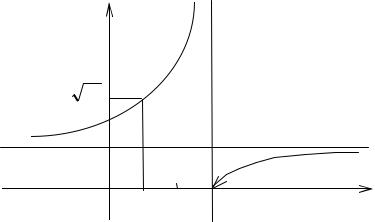
Пример.
y=x3 непрерывна в любой точке х0. Действительно,
lim x3 lim |
x lim |
x lim x x03 y x0 . |
|
x x0 |
x x0 |
x x0 |
x x0 |
Непрерывная функция изменяется постепенно (малые изменения аргумента влекут за собой малые изменения функции).
Если f(x0) 0 и в точке х0 функция непрерывна, то значения функции f(x) в некоторой окрестности точки x0 имеют тот же знак, что и f(x0).
Функция непрерывная в интервале непрерывна в каждой его точке. График непрерывной функции представляет собой сплошную линию без разрывов. Все основные элементарные функции (хn, ax, loga x , тригонометрические функции, обратные тригонометрические функC ции) непрерывны в тех интервалах, в которых они определены.
Определение. Точка х0, в которой функция имеет левый и правый пределы, не равные между собой, называется точкой разрыва первого рода функции f(x). Все остальные точки разрыва называются точками разрыва второго рода.
1 |
|
|
|
|
|
|
|
|
|||||
Так, функция f x 15 |
|
|
|
|
|
|
|
|
|||||
3 x |
|
в точке x = 3 не определена. |
|||||||||||
Односторонние пределы в этой точке |
|
|
|
|
|||||||||
1 |
|
|
15 ; |
|
|
|
|||||||
|
lim 15 |
|
3 x |
|
|
|
|
|
|||||
|
x 3 o |
|
|
|
|
|
|
||||||
|
x 3 3 x 0 |
|
|
|
|
||||||||
1 |
|
|
15 |
1 |
|
|
|
||||||
|
lim 15 |
3 x |
|
0. |
|||||||||
|
15 |
||||||||||||
|
x 3 o |
|
|
|
|
|
|||||||
|
x 3 3 x 0 |
|
|
|
|
||||||||
Точка x1 3 – точка разрыва второго рода (рис. 7). |
|||||||||||||
|
y |
|
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
y 15 |
3 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
2 |
3 |
|
|
|
|
||||
Рис.7
50
