Файловый архив студентов. Файловый архив студентов.
1306 вузов, 5174 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Пензенский Государственный Университет Архитектуры и Строительства
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

1556

.pdf
Скачиваний:
1
Добавлен:
16.06.2024
Размер:
2.17 Mб
Скачать
☆
381

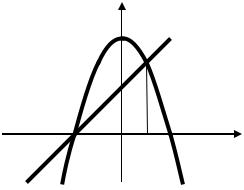
Решение

Изобразим графики указанных кривых на координатной плоскости: y

 

y=4 x2

2

x

y=x+2

0 1 2

Фигура, площадь которой необходимо найти, заключена между кривыми y 4 x2, y x 2 . Абсциссы точек пересечения этих кривых равны 2 и 1. Площадь криволинейной трапеции найдем с помощью

 

 

b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

интеграла

S f1 x f2 x dx .

 

Получим,

что

площадь данной

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

области равна:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

S

4 x2 x 2 dx

4 x2 x 2 dx

2 x2 x dx

2

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ: 4)

2 x2

x dx .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задание 18

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Интеграл 2

 

xdx

 

равен

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1) ln 5 x2

 

5 x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

С;

 

 

 

 

2) ln

 

x2

 

С;

 

 

 

 

 

 

 

 

 

 

3) 2ln 5 x2 С; ;

 

 

 

 

4)

1

ln

 

x2 5

 

С .

 

 

 

 

 

 

 

 

 

 

 

 

2

 

Решение

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Подведем выражение 5 x2

под знак дифференциала:

 

 

 

d 5 x2 5 x2 dx 2xdx .

 

Тогда

 

 

2

 

xdx

 

d 5 x

2

ln 5

x2 C .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

5 x

2

 

 

 

 

 

 

 

 

 

5 x

 

 

 

 

 

 

 

 

 

 

 

 

Ответ: 1) ln 5 x2 С .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 
Задание 19
Числитель общего члена последовательности

32 , 59 , 278 ,... является

членом арифметической прогрессии с разностью d=3, а знаменатель – членом геометрической прогрессии со знаменателем q=3. Указать общий член заданной последовательности

1) c

( 1)n 1

 

3n

;

2)

c ( 1)n

 

n

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

2n 1

 

 

 

n

 

 

 

 

 

 

2n 1

 

 

 

 

 

 

 

3n 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3) c

 

;

 

 

 

 

4) c

 

2n

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

3n

 

 

 

 

 

 

 

 

n

 

 

6n 3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Общий член числителя

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

an a1 d n 1 2 3 n 1 3n 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Для общего члена знаменателя имеем b

3 3n 1

3n .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

Таким образом, общий член всей последовательности равен

 

 

 

 

 

 

 

 

 

 

c

3n 1

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

3n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ: 3) c

3n 1

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

3n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задание 20

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

3

2

 

 

 

 

 

 

 

 

sin n

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Из трех заданных рядов

a)

 

 

;

б)

 

 

 

 

;

в)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2n

1

 

 

 

 

 

n3

 

3n

 

 

 

 

 

 

 

 

n 1

 

 

 

 

 

 

 

 

 

 

 

n 1

 

 

 

n 1

 

 

являются сходящимися:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1) только а);

 

 

2) только б);

 

 

3) только б) и в);

4) только а) и б).

Решение

Все три ряда – знакоположительные. Для выяснения их сходи мости воспользуемся признаками сходимости знакоположительных рядов.

Общий член первого ряда равен

u

 

n3

2

 

. По необходимому

 

 

 

 

 

 

 

 

 

 

n

 

2n 1

 

 

 

 

 

 

 

 

 

 

 

признаку сходимости должны иметь:

 

 

 

 

 

 

 

 

 

lim u

 

lim

n3

2

0 ,

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

n 2n 1

 

 

 

 

 

 

 

 

 

 

 

 

 

Необходимое условие сходимости не выполняется; ряд расходится.

382

 

 

sin n

 

 

1

 

1

 

 

 

 

Для членов второго ряда справедливо:

 

 

 

Ряд

 

 

 

 

 

n3

 

n3

n p

 

 

 

 

 

 

 

 

 

 

 

n 1

 

сходится, если p 1, так что по первому признаку сравнения ряд

–

б)

сходится (p=3>1)

Третий ряд, составленный из членов бесконечно убывающей геометрической прогрессии, так же сходящийся.

Ответ: 3) только б) и в) .

Задание 21

 

 

 

 

 

x

n

 

 

Радиус сходимости степенного ряда

 

 

равен:

2n

 

 

 

 

 

n 1

1

1) 0;

2) 2;

3)

1

;

4) 1.

2

 

 

 

 

 

 

 

 

Решение

Для отыскания радиуса сходимости степенного ряда воспользуемся

формулой

R lim

 

an

 

 

 

.

В

 

данном

ряде

a

 

 

1

 

,

тогда

 

 

 

 

 

n

a

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

2n 1

 

 

 

 

 

 

 

 

 

 

n 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

an 1

 

1

 

 

 

1

 

 

. Найдем радиус:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n 1 1

2n 3

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

1

 

2n 3

 

 

 

 

 

 

 

 

 

 

 

 

R lim

 

 

 

 

 

 

 

:

 

lim

 

1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

2n 1

2n 3

n 2n 1

 

 

 

 

 

 

 

Ответ: 4) 1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задание 22

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y 0

 

Общее

решение дифференциального

уравнения

 

имеет

y

вид…

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1) y C ex , C R ;

 

 

 

 

 

 

 

 

2) y Cex , C R ;

 

 

 

 

 

 

 

3) y C ex ,C R ;

 

 

 

 

 

 

 

 

4) y Cx,C R .

 

 

 

 

 

 

 

Решение

Данное уравнение является дифференциальным уравнением I го порядка с разделяющимися переменными. Действительно, с учетом y dxdy получим

dxdy y 0 ; dxdy y .

383

 

Откуда

 

 

 

 

 

 

 

 

 

 

dy

dx ,

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

dy

dx, ln

 

y

 

x C или y ex C

или y Cex (принято C eC ).

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ: 2) y Cex ,C R .

 

 

 

Задание 23

 

 

Общее решение дифференциального уравнения y sin3x имеет вид…

1)y 271 cos3x C1x C3 ;

2)y 1 cos3x C1 x2 C2 x C3 ; 27 2

3)

y

1

cos3x C

x2

C

 

x C

 

;

27

2

 

 

 

 

 

1

 

2

 

3

 

4)

y

1

cos3x C .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

27

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение

Заданное уравнение – третьего порядка. Будем постепенно понижать порядок, интегрируя обе части уравнения по х.

y sin 3xdx 13 cos3x C1 ;

 

 

 

1

 

 

1

 

 

 

 

 

y

 

 

 

cos3x C1 dx

 

sin3x C1x C2, где С1, C2 R ;

3

9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

1

 

x2

y

 

 

 

sin3x C1x C2 dx

 

cos3x C1

 

C2 x C3 ,

9

27

2

 

 

 

 

 

 

 

 

 

где С1, C2, C3 R .

 

 

 

 

 

 

 

Ответ: 2) y

1

cos3x C

x2

C

x C

 

.

27

2

 

 

1

2

 

3

 

384

Задание 24

Общее решение линейного однородного дифференциального урав нения второго порядка y 6y 5y 0 имеет вид…

1) y ex e5x ;

2) y C ex e5x ;

 

 

 

 

1

 

 

3) y C x C

2

5x ;

4) y C ex

C

e5x .

1

 

1

2

 

Решение

 

 

 

 

 

Характеристическое уравнение имеет вид:

 

 

 

 

k2 6k 5 0 .

 

Корни этого уравнения: k1 1, k2 5 . Так что, общее решение диф

ференциального уравнения представляется в виде:

y C ex C

e5x .

 

 

 

 

 

 

 

1

2

 

Ответ: 4)

y C ex C

e5x .

 

 

 

 

 

 

1

2

 

 

 

 

 

 

Задание 25

 

 

 

 

 

 

 

Найти вероятность

 

p2 , если дискретная случайная величина X

задана рядом распределения

 

 

 

 

xi

 

1

 

 

2

3

 

 

4

pi

 

0,3

 

 

p2

0,1

 

 

0,2

1) 0,1;

 

2) 0,2;

 

3) 0,3;

4) 0,4.

 

 

 

Решение

 

 

 

 

 

 

 

 

Для дискретной случайной величины сумма вероятностей всех возможных значений равна единице. Поэтому

0,3 p2 0,1 0,2 1.

Откуда p2 0,4 . Ответ: 4) 0,4.

Задание 26

Случайная величина X задана рядом распределения

Х

 

1

 

 

0

 

1

p

 

0,2

 

 

0,3

 

0,5

Тогда дисперсия D(Х) равна...

 

 

 

 

1) 0,7;

2) 0,49;

3) 0,61;

4) 2,4.

 

Решение

 

 

 

 

 

 

 

По известной формуле для дисперсии:

 

 

 

 

D Х M

Х 2 M Х 2 .

 

 

 

 

 

 

 

385

Математическое ожидание

n

MХ xi pi 1 0,2 0 0,3 1 0,5 0,3 .

i 1

Математическое ожидание случайной величины Х 2 определится в виде:

M Х 2 n x 2 p 1 2 0,2 02 0,3 12 0,5 0,7 .

i i i 1

Тогда искомая дисперсия равна D Х 0,7 0,32 0,7 0,09 0,61. Ответ: 3) 0,61.

Задание 27

В магазине формируются подарочные наборы из конфет 5 видов в коробках, по три разных коробки в каждом наборе. Сколькими способами это можно сделать?

1) 10;

2) 15;

3) 5!;

4) 53.

Решение

Здесь одна комбинация будет отличаться от другой только соста вом элементов, порядок расположения безразличен. Количество всех возможных комбинаций – это число сочетаний из пяти элементов по 3.

C 3

 

5!

 

 

4 5

10 .

3! 5 3 !

 

5

 

2

 

 

 

 

Ответ: 1) 10.

Задание 28

Определить значение а, если данная гистограмма частот построена по выборке объемом n=50?

ni

h

a

 

 

 

 

 

16

 

 

 

 

 

12

 

 

 

 

 

4

 

 

 

 

 

0

1

2

3

4

xi

1) 20;

2) 18;

 

3) 17;

4) 19.

 

386

Решение

Так как шаг h 1, то на вертикальной оси гистограммы фактически отмечены частоты значений. Их сумма, как известно, должна быть равна объему выборки: 4 12 16 a 50. Значит, а=18.

Ответ: 2) 18.

Задание 29

Мода вариационного ряда 2, 3, 4, 5, 5, 5, 6, 7, 7, 9, 12, 13 равна … 1) 13 ; 2) 5; 3) 7 ; 4) 9 .

Решение

Мода – варианта с наибольшей частотой. Из всех вариант чаще всего в выборке встречается число 5.

Ответ: 2) 5.

Задание 30

 

 

 

 

 

Уравнение линии

2x2 2y2 72

в полярных координатах имеет

вид…

 

 

 

 

 

1) cos 36 ;

 

2) 72 ;

3) 6;

4) sin 36 .

Решение

 

 

 

 

 

Перейдем

к

полярным

координатам

по

формулам

x cos , y sin . Тогда исходное уравнение примет вид: 2 2 cos2 2 2 sin2 72 ;

2 2 cos2 sin2 72 ; 2 2 72 ;

2 36 .

Так как 0 , то уравнение примет вид 6 . Ответ: 3) 6 .

Задание 31

Имеются две урны, в первой – 5 белых и 5 черных шаров, во вто рой – 3 белых и 7 черных шаров. Из наудачу взятой урны вытаскивается один шар. Тогда вероятность того, что этот шар ока

жется белым равна...

 

 

1) 0,55

2) 0,11;

3) 0,5;

4) 0,4.

387

Решение

Обозначим события:

А – извлечение белого шара; В1 – выбор первой урны В2 – выбор второй урны

Найдем условные вероятности P A / B1 105 , P A / B2 103 . Вы

бор урн равновозможен, то есть P B1 P B2 12 . Тогда по формуле полной вероятности:

P A P A / B1 P B1 P A / B2 P B2 105 12 103 12 0,4 . Ответ: 4) 0,4

Задание 32.

Значение производной функции f (z) 2 z3 в точке z

0

i равно

 

2) 3 ;

3) 2 3i ;

 

 

1) 3 ;

4) 5i .

 

 

Решение

 

 

 

 

 

Найдем производную от данной функции f z 3z2

в точке z0 i

f i 3i2 3

Ответ: 1) 3 .

388

ЗАКЛЮЧЕНИЕ

Пособие предназначено студентам, обучающимся по направлению подготовки 270800 (квалификация выпускника – бакалавр), и напи сано с учетом требований Федерального государственного образова тельного стандарта третьего поколения. Пособие содержит контроль ные тесты (30 вариантов) с решениями примерных задач и тезисное изложение необходимого для их решения теоретического материала, список рекомендуемой литературы.

Оно позволяет осуществлять оценку текущего контроля успевае мости и промежуточную аттестацию студентов по математике в соот ветствии с «Положением о балльно модульно рейтинговой системе оценки качества освоения студентами основных образовательных программ».

Издание может использоваться и в системе открытого образования по различным направлениям подготовки в технических вузах.

389

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Бугров, Я.С. Высшая математика. Т.1. Элементы линейной алгебры и аналитической геометрии [Текст] / Я.С. Бугров, С.М. Никольский. – М.: Дрофа, 2004. – 288 с.

2.Бугров, Я.С. Высшая математика. Т.2. Дифференциальное и интегральное исчисление [Текст] / Я.С. Бугров, С.М. Никольский. – М.: Дрофа, 2004. – 512 с.

3.Бугров, Я.С. Высшая математика. Т.3. Дифференциальные уравнения. Крат ные интегралы. Ряды. Функции комплексного переменного [Текст] / Я.С. Бугров, С.М. Никольский. – М.: Дрофа, 2004. – 512 с.

4.Пискунов, Н.С. Дифференциальное и интегральное исчисления [Текст]: учеб. пособие. Т. 1, 2 / Н.С. Пискунов. –М.: Интеграл Пресс, 2008. – 415 с.

5.Бермант, А.Ф. Краткий курс математического анализа [Текст]: учеб. посо бие / А.Ф. Бермант, И.Г. Араманович. – 15 е изд., стер. – СПб.: Лань, 2009. – 736 с.

6.Данко, П.Е. Высшая математика в упражнениях и задачах [Текст]: учеб. пособие для вузов. Ч.1, 2 / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Оникс 21 век: Мир и образование, 2009. – 304 с. (416 с).

7.Вентцель, А.Д. Теория вероятностей [Текст]: учебник для вузов / А.Д. Вентцель. – М.: Высшая школа, 2010. – 575 с.

8.Беклемишев Д.В. Сборник задач по аналитической геометрии и линейной алгебре [Текст] / Д.В. Беклемишев [и др.]. – СПб.: Лань, 2011. – 496 с.

9.Берман, Г.И. Сборник задач по курсу математического анализа. Решение типичных и трудных задач [Текст]: учеб. пособие / Г.И.Берман. – 3 е изд., стер. – СПб.: Лань, 2007. – 604 с.

10. Боревич З.И. Определители и матрицы [Текст]: учеб. посо бие. –5 е изд., стер. – СПб.: Лань, 2009. –184 с.

11.Бутузов, В.Ф. Линейная алгебра в вопросах и задачах [Текст] / В.Ф. Бу тузов, Н.Ч. Крутицкая, А.А. Шишкин. – М.: Лань, 2010. – 256 с.

12.Бутузов, В.Ф. Математический анализ в вопросах и задачах [Текст] / В.Ф. Бутузов [и др.]. – СПб.: Лань, 2010. – 480 с.

13.Вентцель, А.Д. Теория вероятностей и ее инженерные приложения [Текст] / А.Д. Вентцель. – М.: Академия, 2010. – 464 с.

14.Владимирский, Б.М. Математика. Общий курс [Текст]: учебник / Б.М. Владимирский, А.Б. Горстко, Я.М. Ерусалимский. – 4 е изд., стер. – СПб.: Лань, 2008. – 957 с.

15.Воеводин В.В. Линейная алгебра [Текст] / В.В. Воеводин. – СПб.: Лань, 2010. – 416 с.

16.Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике [Текст]: учеб. пособие / В.Е. Гмурман. – М.: Высшая школа, 2006 – 476 с.

17.Данилов, А.М. Теория вероятностей и математическая статистика с инже нерными приложениями [Текст]: учеб. пособие / А.М., Данилов И.А. Гарькина. – Пенза: ПГУАС, 2010. – 228 с.

18.Демидович, Б.П. Дифференциальные уравнения [Текст] / Б.П. Демидо вич, В.П. Моденов. – СПб.: Лань, 2008. – 288 с.

19.Запорожец Г.И. Руководство к решению задач по математическому анализу [Текст]: учеб. пособие / Г.И. Запорожец. – 6 е изд., стер. –СПб.: Лань, 2010. – 460 с.

20.Зубков, А.М. Сборник задач по теории вероятностей [Текст] / А.М. Зуб ков, Б.А. Севастьянов, В.П. Чистяков. – СПб.: Лань, 2009. – 320 с.

390

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности