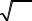Файловый архив студентов. Файловый архив студентов.
1306 вузов, 5174 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Пензенский Государственный Университет Архитектуры и Строительства
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

1556

.pdf
Скачиваний:
1
Добавлен:
16.06.2024
Размер:
2.17 Mб
Скачать
☆

25. Случайная величина Х задана плотностью распределения

 

1

е

 

( х 2)2

 

 

 

f(x) =

18

 

. Тогда D(2х + 1)

равна

 

 

 

 

 

3 2

 

 

 

 

1) 16;

 

2) 32;

3) 36;

4)

28.

26. Для функции z 3y3 5xy2 7x 8 укажите верное утверждение:

1) z 9y2 ;

y

2) z z 27y2 7 ;x y

3) z 7 ;

x

4)z 9y2 10xy .

y

27. Чему равно значение а, если данная гистограмма частот по= строена по выборке объемом n=100?

ni

h

 

36

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

32

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

24

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xi

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

1

 

 

 

 

2

 

 

 

3

 

 

4

 

 

 

 

 

1) 10;

 

 

 

2) 8;

 

 

 

 

 

 

 

 

 

3) 6;

 

 

 

 

 

4) 7.

 

 

28. Общий член ряда

1

 

1

 

 

1

 

 

1

 

... имеет вид:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

9

 

27

 

 

81

 

 

 

 

 

 

 

 

 

1 n 1

 

 

( 1)n

 

 

 

 

 

1 n

 

 

3) un

 

1

 

 

 

 

 

 

1)

un

 

 

;

2) un

 

 

;

 

 

 

 

;

 

4)

un

 

 

 

.

 

 

 

 

 

 

3

n 1

3

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

3

29. Число 7 2i является…

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1)

комплексным;

 

 

 

2) целым;

 

 

 

 

 

 

 

 

 

 

 

 

 

3)

рациональным;

4) иррациональным.

 

 

 

 

 

 

 

 

231

30. Сколько точек разрыва у функции y

x 5

?

 

x 5 2 x 1 3 x

1) 1;

2) 2;

3) 6;

4) 3.

31. В первой коробке 7 стандартных и 3 бракованных детали, а во второй коробке 5 стандартных и 5 бракованных деталей. Из произ= вольной коробки наугад вынимают одну деталь. Какова вероятность того, что эта деталь стандартная?

1)

1

;

2)

0,6 ;

3)

0,5;

4) 0,7 .

12

 

 

 

 

 

 

 

32.

Мода вариационного ряда 5, 5, 5, 5, 6, 7, 7, 7, 9, 12, 12, 13 равна …

1) 13 ;

2)

5;

3)

7 ;

4) 9 .

33.

Уравнение x 2 y2 x в полярных координатах имеет вид…

1)

cos ;

2)

cos ;

3)

2 2 ;

4) sin 1.

232

 

 

 

 

Вариант 5

 

 

6

0

4

 

 

 

 

1. Определитель

 

2

3

5

 

равен

 

 

1

0

1

 

 

 

 

 

 

 

 

 

1)

30;

2) 6;

3) 0;

 

4) 18.

 

 

 

2. Если

7

4

1

1

 

 

 

 

А =

и

В =

, то матрица 4А – 2В равна

 

 

 

 

 

3

2

1

2

 

 

 

 

1)

26

14

26

1

3)

26

14

26

14

 

;

2)

;

 

;

4)

.

 

10

1

10

12

 

10

15

10

12

3. 2

 

для Z = =3 – 4i равно

 

 

 

 

 

 

 

 

 

 

 

1)

=6+6i;

2) =6=8i;

3) =6+8i;

 

4) 6=8i.

 

10. Модуль комплексного числа z = 3 – 4i равен

 

 

1)

3;

 

2) =5;

3) 0;

 

4) 5.

 

 

 

11.

Величины отрезков, отсекаемых прямой 2х – 3у – 6 = 0 на осях

координат равны:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1) а = 3, b = 2;

 

2) а = 2, b = =3;

 

3) а = 3, b = =2;

4) а = =2, b = =3.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

12.

Если

а

= 3

i

– 5

j

+ 7

k

, то

 

a

 

равен

 

 

 

 

 

 

 

 

 

 

1)

9;

2)

83;

3)

63;

4)

83.

 

 

 

13.

Из плоскостей

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a) 2x + 3z – 2 = 0; b) y – 5 = 0;

 

c) x + 13 = 0;

d) z – 1 = 0

перпендикулярны оси OY:

 

 

 

 

 

 

 

 

 

1)

а) и с) ;

2)

только b);

 

3) ни одна;

4)

a) и b).

14.

Уравнение х2 + у2 – 6х + 8у – 11 = 0 определяет на плоскости

1)

 

параболу;

2) гиперболу;

 

 

 

 

3) окружность;

4) эллипс.

15.

 

Каноническое

 

уравнение окруж=

y

 

 

 

 

 

 

 

ности, изображенной на рисунке, имеет

 

 

 

вид:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

2

x

1) (х – 2)2 + (у + 2)2 = 1;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2)

(х – 2)2 + (у+2)2 = 2;

 

 

 

 

 

 

 

 

 

3)

(х+2)2 + (у=2)2 = 4;

 

 

 

 

 

 

2

 

 

4)

(х=2)2+(у+2)2=4.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

233

10. Функция y = 3х – 2 отображает множество 2;3 на множество 1) 3;2 ; 2) 3;2 ; 3) 7;25 ; 4) 9;24 .

11. Предел

lim

3n2 2n 1

равен

 

5n n2

 

 

 

 

n

 

 

 

 

1) 2;

2) 3;

 

3) =3;

4) =1.

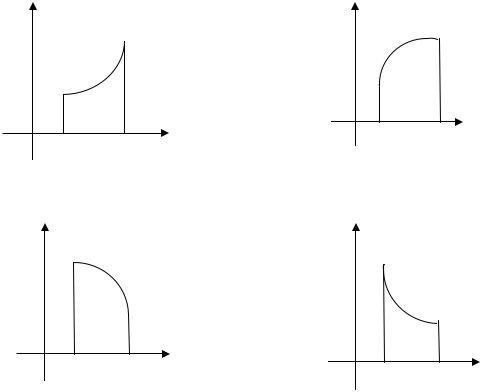
12. График какой функции на всем отрезке а;в одновременно удовлетворяет трем условиям: y y 0, y 0 ?

y

y

 

 

x

 

x

 

 

 

 

0

a

0

a

b

b

 

 

Рис.1

Рис.2

y

y

 

 

 

x

 

x

 

 

 

 

 

0

a

b

0

a

b

 

 

 

 

Рис.3

 

 

 

 

 

Рис.4

 

1) только 2;

2) 1 и 2;

 

 

3) все графики;

4) только 3.

13. Если z = arctg

x

, то z

 

в точке М(=4;3) равна

 

 

x

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

1) 1;

2) ;

3)

0,12;

4) 1,2.

 

234

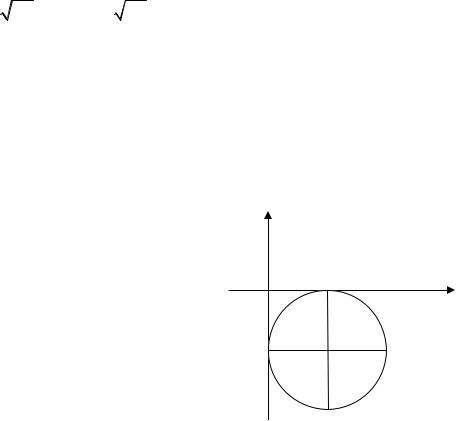
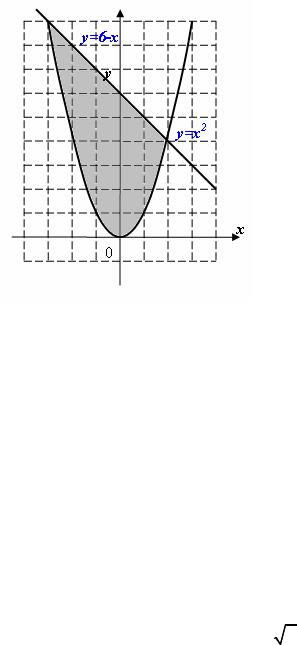
14. Площадь заштрихованной части фигуры, изображенной на чертеже, задана интегралом

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1) (1 х х 2 )dx

 

 

 

 

 

 

2) (6 x x 2 )dx;

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3)

 

(6 x x 2 )dx;

 

 

 

 

 

4) (6 x 2 )dx.

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

15. Интеграл

 

 

xdx

 

равен

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3x

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1)

 

ln

 

3x 2

2

 

 

+ C;

 

 

 

 

2)

 

ln

 

3x 2

 

2

 

C;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3)

 

 

1

ln

 

3x 2

2

 

C;

 

 

 

 

4)

 

 

1

arctg

x

+ C.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3n 2 n

 

 

 

3

 

 

 

 

 

 

 

( 1)n 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

16.

 

 

Из рядов а)

 

 

 

 

 

; б)

 

 

 

;

 

в)

 

 

 

расходятся

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n 1

 

2n 1

 

 

 

 

 

 

n 1 n2

 

 

 

 

n 1

 

n

1)

только а);

 

 

 

2)

а) и в);

 

 

 

 

3) все;

 

 

 

 

 

 

4) только в).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

n

17.

 

 

Радиус сходимости степенного ряда

 

 

 

 

 

 

 

n2 3n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n 1

 

 

 

 

 

1)

2;

 

 

 

 

 

2) 3;

 

 

 

 

 

3)

1;

4) 0.

 

 

 

 

 

 

18.

 

 

Дифференциальное уравнение у – у + 3 = 0 по виду

1)только однородное;

2)только линейное;

235

3)только с разделяющимися переменными;

4)линейное и с разделяющимися переменными.

19. Частное решение дифференциального уравнения (1+х2) y =2х (4 – у), если у(0) = 1, имеет вид:

1) y = 4 –

 

3

;

2) y =

 

4х 2 1

; ; 3) y = 4 +

 

1

; 4) y =

 

4х 2

.

 

 

 

 

 

 

 

 

 

 

 

х 2

 

х 2 1

 

 

х 2

1

х 2

 

1

 

 

 

 

 

1

 

 

20. Общее решение дифференциального уравнения у

– 4у = 0

имеет вид:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1) у = С

е4х

+ С е=4х;

2) у = С

е=4х + С

хе=4х;

 

 

 

 

 

1

 

 

2

 

 

 

 

 

1

2

 

 

 

 

 

 

 

 

3) у = С1 + С2 е4х;

 

4) у = С1е4х + С2хе4х.

 

 

 

 

 

 

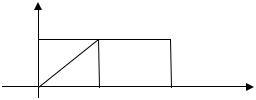
21. Расставить пределы интегрирования в двойном интеграле по области, изображенной на чертеже

y

1

x

 

 

0

1

2

 

 

 

 

1

2

 

2

1

 

 

 

1) dy f (x, y)dx;

2) dx f (x, y)dу;

 

 

 

0

y

0

0

 

 

 

 

2

1

 

1

2

 

 

 

3) dy f (x, y)dx;

4) dy f (x, y)dx.

 

 

 

0

0

 

0

x

 

 

22. Найти р3, если дан ряд распределения

 

 

 

х

 

3

 

 

6

 

12

24

 

р

 

0,2

 

 

0,1

 

р3

0,5

1)

0,9;

2) 0,7;

3) 1;

4) 0,2.

 

 

23. Случайная величина Х распределена по нормальному закону с параметрами а и . По результатам наблюдаемых значений 35, 15, 5, 25, 5 оценить параметр а.

1) 19; 2) 15; 3) 17; 4) 20.

236

24.

Даны две случайные величины Х и Y.

 

 

 

 

 

 

 

 

 

 

 

 

 

Х

 

=1

 

0

 

 

1

 

 

 

 

 

 

 

 

 

 

 

р

 

0,2

 

0,3

 

 

0,5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Y

 

0

 

 

 

1

 

2

 

 

3

 

 

 

 

 

 

 

р

 

0,1

 

0,2

 

0,3

 

0,4

 

Тогда М(Y –2Х) равно

 

 

 

 

 

 

 

 

 

 

 

 

1) 1,4;

 

2) 0,8;

 

3) 1,7;

 

4) 3,2.

 

 

 

 

25.

Случайная величина

 

Х задана

плотностью распределения

f(x) =

1

е

( х 2)2

. Тогда дисперсия D(2х + 1) равна

 

18

 

3 2

 

 

 

1) 16;

 

2) 32;

 

 

3) 36;

 

 

4)

28.

 

 

 

26.

Для функции

z 5x 3

4y2

x 3 y2

4xy укажите верное утвер=

ждение:

1)z 15x 2 ;

x

2)z 8y ;y

3)z 3x 2 y2 15x 2 4y ;

x

4)z 2x 3 y 12x 2 10y .

y

27. Двусторонняя критическая область может определяться из соотношения…

1)z 2x 3 y 12x 2 10y ;

y

2)P K 2,5 P K 2,5 0,05 ;

3)P K 2,5 0,05 ;

4)P 2,5 K 2,5 0,95 .

28. В партии из 8 деталей 3 бракованные. Наудачу отобраны две детали. Тогда вероятность того, что обе детали будут бракованными, равна…

1)

1

;

2)

1

;

3)

3

;

4)

3

.

2

4

8

28

 

 

 

 

 

 

 

 

 

 

 

 

 

 

237

 

 

 

 

 

29. Выборочное уравнение прямой регрессии Y на X имеет вид y 3 2,2x . Тогда выборочный коэффициент корреляции может быть

равен…

1)

2,2;

2)=2,2;

3) =0,3;

4)

0,3.

 

 

30. Смешанное произведение векторов

 

2; 4;1 ,

 

 

3; 5; 2 ,

 

 

 

b

a

 

 

1; 9; 1 равно…

 

 

 

 

 

 

 

 

 

c

 

 

 

 

 

 

 

 

 

1)

10;

2)

5;

3) 3;

 

 

4)

0.

 

 

31. Максимум функции f x 2x 3

15x 2 36x равен …

 

1)

=3;

2)

=2;

3) 0;

 

 

4)

36.

32. Для уборки снега используются снегоуборочные машины. Они работают в течение суток с постоянной скоростью уборки снега 400 м3/ч. Изменение объема снега, выпадающего на улицы города в

течение суток, можно описать уравнением dSdt 620 20t , где S t –

объем снега (в м3), выпавшего за время t (в часах), 0 t 24 . В момент времени t=0 на улицах города лежит 1000 м3 снега. Чему равен объем снега, лежащего на улицах, в момент времени t=6?

1) 2200; 2) 1960; 3) 2160; 4) 1900.

33.

Основная гипотеза H

0

: 2

3 . Тогда конкурирующей может

 

 

 

 

 

 

 

 

являться гипотеза…

 

 

 

 

 

 

 

1)

H : 2 4 ;

2) H : 2 3 ;

3) H : 2

5 ;

4) H : 2

3 .

 

1

1

 

 

1

 

1

 

238

 

 

 

Вариант 6

 

1

2

3

4

 

 

 

1. Определитель

0

2

5

9

равен …

 

0

0

3

7

 

 

2

4

6

0

 

1) =48;

 

2)9;

 

 

3) 12;

 

 

 

4) 48.

 

 

 

 

 

 

2.

 

 

2 1

1

 

 

2

1

0

3A 2B равно

Если A

 

 

 

 

и B

 

 

 

, то

 

 

 

0 1

4

 

 

 

3

2 2

 

 

 

 

 

 

1)

0 2

 

1

; 2)

 

2

5 2

; 3)

2 5

3

 

0

6 3

 

 

 

 

 

 

 

 

 

 

; 4)

 

 

 

.

 

3 3

 

2

 

 

 

9

8 2

 

 

6 7

8

 

9

9 6

3.

Если z 3 8i , то

 

равно

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

1) 3 8i ; 2) 3 8i ;

 

 

3) 3 8i ;

 

4) 73 .

 

 

 

 

 

 

4.

Если z

 

1

1

i и

z

 

1 5i ,

то модуль комплексного числа

 

 

2

 

1

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2z1 z2 равен

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1) 6;

2) 5;

 

 

 

 

 

3) 4;

 

 

 

4) 3.

 

 

 

 

 

 

5.

Производная от функции f z 2z3 3i в точке z

1 3i равна

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

1) =48=36i;

 

 

 

2) 10=6i;

 

 

 

 

3) 60=36i;

 

4) 0.

6.

При каком значении векторы a( , 3, 2) и b(1, 2, )взаимно

перпендикулярны?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1) 6;

2)=6;

 

 

 

 

3) 1;

 

 

 

4)=2.

 

 

 

 

 

 

7.

Уравнение прямой, которая отсекает на осях координат равные

отрезки a b 3

 

 

 

 

 

 

 

 

 

 

 

 

 

4) 3x 3y 1 0.

1) x y 3 0 ;

2) x y 3 0 ;

3) 3x 3y 1 0 ;

8.

Даны координаты вершин треугольника A(1, 2),

B( 5, 3),

C(7, 6). найти точку, делящую пополам медиану AD

 

 

 

 

 

1)( 2; 0,5);

2)(4; 2) ;

 

 

 

 

(1; 4,5) ;

 

 

 

5

 

 

 

 

3)

4)

1;

 

 

.

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

9.

Какие из данных плоскостей параллельны оси ординат

 

239

а) 5x 3y z 0 , б) 2x 5z 7 0 , в) 2x 3 0 , г) y 0, y 0, y 0

1)

ни одна;

2)только б) и в);

3) только б);

4)

только а) и в).

10.

Уравнение 4x 2 4y2 4x 8y 11 0 определяет на плоскости

1)

прямую;

2) плоскость;

3) эллипс;

4)

окружность.

11.

Составить простейшее уравнение гиперболы,

если ее фокусы

лежат на оси абсцисс, и расстояние между ними равно 20. Действи= тельная ось гиперболы равна 16.

 

x 2

 

y2

 

x 2

 

y2

x 2

y2

x 2

y2

1)

 

 

 

1;

2)

 

 

 

1; 3)

 

 

 

1; 4)

 

 

 

1.

8

10

36

64

64

36

10

8

 

 

 

 

 

 

 

 

 

 

12. Вычислите предел lim

 

x 3 x 2 x 1

 

 

 

 

 

x 2 4x 3

 

 

 

 

 

 

x 1

 

 

 

 

1)=1;

2) ;

3)

1

;

 

4) 1.

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

1

 

 

 

 

13.

Вычислите предел lim

 

 

 

 

 

 

 

.

 

 

 

x 2

 

 

 

 

x 2

x 2 4

 

 

1) 0;

2)

1

;

3)

 

1

;

 

 

4)

1

.

 

 

 

 

 

 

 

4

 

 

 

4

 

 

 

 

2

 

 

14. Даны графики прямых… y

f

h

 

 

 

g

 

 

0

1

 

 

 

 

 

 

 

 

x

 

u

 

 

 

 

Расположите прямые в порядке возрастания их угловых коэф=

фициентов

 

 

 

 

1) u, g, f, h;

2) h, f, u, g;

3) g, u, f, h;

4) f, h, u, g.

240

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности