
1556
.pdf
Пример. Вычислить интеграл |
|
|
|
dx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Используя универсальную тригонометрическую подстановку, |
|||||||||||||||||||||||||||||||||||||||
имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
dx |
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
d |
t |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||
2 |
sin x |
|
|
|
2 |
|
|
|
2t |
|
|
|
|
|
|
t |
2 |
t 1 |
|
|
1 |
|
2 |
|
3 |
|
|||||||||||||
|
|
|
|
|
|
|
1 t |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
2t 1 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
x |
|
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
arctg |
|
|
|
|
C |
|
|
|
|
arctg |
|
|
tg |
|
|
|
|
C . |
|
|
|
||||||||||||
|
|
|
3 |
|
|
3 |
|
3 |
|
|
3 |
|
2 |
3 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Если подынтегральное выражение зависит от sin2 x, cos2 x |
или от |
||||||||||||||||||||||||||||||||||||||
tgx , применяется подстановка t tgx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Интегрирование простейших иррациональностей |
|
|
|
||||||||||||||||||||||||||||||||||
1. Если подынтегральное выражение содержит только линейную |
|||||||||||||||||||||||||||||||||||||||
иррациональность m ax b |
a 0 |
, то |
|
используется |
|
подстановка |
|||||||||||||||||||||||||||||||||
t m ax b .
Интеграл от простейшей квадратичной иррациональности |
|
dx |
|
2 |
|
|
ax |
bx c |
после выделения полного квадрата в трехчлене ax2 bx c сводится к
одному из двух интегралов |
|
|
|
|
|
dx |
|
|
( 0 ), |
|
dx |
|
( a 0 ). |
|||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
2 |
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
a |
x |
|
|
||||||
Используя подстановку Эйлера |
|
|
x2 t x , найдем |
|||||||||||||||||||||||||
|
dx |
ln |
|
x x2 |
|
C 0 . |
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
dx |
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
x |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Второй интеграл |
|
|
|
|
|
|
|
|
|
a |
|
arcsin |
C . |
|||||||||||||||
a |
2 |
x |
2 |
|
|
|
|
|
|
x |
2 |
a |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
||||||
Определенный интеграл
Площадь криволинейной трапеции. Пусть на отрезке a,b задана непрерывная функция y f x 0 . Найдем площадь криволинейной трапеции ABCDA. Для этого разобьем отрезок a,b на n частичных
91

отрезков |
x0 , x1 , x1, x2 , , xn 1, xn . В каждом |
частичном отрезке |
|||
xi 1, xi , |
i |
|
возьмем произвольную точку i |
и вычислим f i . |
|
1,n |
|||||
Значение |
f i |
xi , |
xi xi xi 1 равно площади прямоугольника с |
||
|
n |
основанием xi и высотой |
f i . Тогда сумма Sn f i xi равна |
|
i 1 |
площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции. При уменьшении всех величин xi точность
приближения увеличивается. Поэтому за точное значение S площади криволинейной трапеции принимается предел S , к которому стремится площадь Sn , когда n неограниченно возрастает так, что max xi 0 :
|
|
n |
S lim Sn |
lim f i xi . |
|
n |
n |
i 1 |
|
0 |
|
y
B |
|
A |
1 |
|
|
x0 |
x1 |
C y=f(x)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
n |
|
|
D |
|
|
x2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
… |
xnC1 b=xn |
x |
|||||||
О п р е д е л е н и е . ких, что max xi 0 , гральная сумма
Если при любых разбиениях отрезка [a,b], таC и при любом выборе точек i xi 1, xi интеC
n
Sn f i xi i 1
стремится к одному и тому же пределу, то этот предел называют оп3 ределенным интегралом от функции f(x) на отрезке [a,b] и обозначают
b |
|
n |
f x dx |
lim |
f i xi , |
a |
max xi 0 |
i 1 |
|
92
где a, b – нижний и верхний пределы интегрирования.
Определенный интеграл от неотрицательной функции численно равен площади S криволинейной трапеции.
Если для f(x) существует предел интегральной суммы, то ее называют интегрируемой на [a,b].
Если f(x) интегрируема на [a,b], то площадь криволинейной трапеC
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
ции на [a,b] равна f x dx. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
Теорема. Если функция f(x) непрерывна на [a,b], то она интегриC |
||||||||||||||||
руема на [a,b]. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Cвойства определенного интеграла |
||||||||
|
b |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
1. |
cf x dx c f x dx, |
c const . |
||||||||||||||
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n b |
2. |
f1 x f2 x fn x dx fj x dx . |
|||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 a |
|
b |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
3. |
f |
x dx f x dx . |
|
|
|
|||||||||||
|
a |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
a |
|
x dx 0 . |
|
|
|
|
|
|
|
|
|||||
4. |
f |
|
|
|
|
|
|
|
|
|||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
b |
|
|
|
|
|
b |
|
|
|
5. |
|
f |
x |
dx |
|
f |
y |
dy |
|
f |
||||||
|
|
|
|
|
|
|
|
t dt . |
||||||||
|
a |
|
|
|
|
|
a |
|
|
|
|
|
a |
|
|
|
6. |
Если на [a,b], где a<b, функции f(x) и (x) удовлетворяют |
|||||||||||||||
условию f(x) (x), то |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
f x dx x dx. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
a |
7. |
Если на [a,b] |
имеют место неравенства m f x M , то |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
m b a f x dx M b a . |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
8. |
Теорема о среднем. |
|
|
|
|
|||||||||||
Если f(x) непрерывна на [a,b], то найдется такое a,b , что
b
f x dx b a f .
a
93
9. Для любых трех чисел a,b,c; a< c< b справедливо
b |
c |
b |
f x dx f x dx f x dx, |
||
a |
a |
c |
если только все три интеграла существуют (аддитивное свойство интеграла).
|
b |
|
b |
|
||||
|
|
|
||||||
10. |
f x dx |
|
|
|
f x |
|
dx, |
a b . |
|
|
|
||||||
|
|
|
|
|
||||
|
a |
|
a |
|
||||
11. Интегрирование четных и нечетных функций по отрезку вида |
||
a,a : |
|
|
если f x – четная функция, то |
a |
a |
f x dx 2 f x dx. |
||
|
a |
0 |
a
если f x – нечетная функция, то f x dx 0 .
a
12. Дифференцирование интеграла по переменному верхнему преC делу.
|
|
|
x |
Если f x |
непрерывна на a,b , то функция x f t dt дифC |
||
|
|
|
a |
ференцируема на a,b , причем x f x , то есть |
|||
|
x |
|
|
|
|
f x . |
|
|
|
|
|
|
|
f t dt |
|
|
a |
|
|
13. Формула НьютонаCЛейбница:
b
f x dx F x |ba F b F a ,
a
где F x – какаяCнибудь первообразная для функции f x на a,b .
14. Интегрирование по частям
b |
b |
||
udv uv |
|
ba |
vdu . |
|
|||
|
|||
a |
a |
||
15. Интегрирование подстановкой (заменой переменного)
94

Если f(x) непрерывна на [a,b], то, введя переменную t по формуле x t , где a; b; (t) непрерывна на [ , ]; f t опреC
b |
|
делена и непрерывна на [a,b], получим f x dx f t t dt . |
|
a |
|
Вычисление определенного интеграла
Непосредственное вычисление
2
sin xdx cos x 02 cos2 cos0 1 1 0.
0
Интегрирование подстановкой (заменой переменного)
b |
|
|
|
|
|
x a sin t; dx a costdt. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 x2 dx |
x 0 t 0 |
|
|
|
|
|
|
||||||||||||||
a |
|
|
|
|
|
x |
a t |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
a2 a2 sin2 t a cos tdt a2 2 cos2 tdt |
|
|||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
1 cos2 t |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
1 |
2 |
|
|
|
|
||
a2 |
|
|
|
|
dt a2 |
|
|
dt |
|
cos2tdt |
|
||||||||||
2 |
|
|
2 |
|
2 |
||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
a2 |
|
|
|
|
|
|
|
a2 |
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|||||||
|
|
t |
|
|
|
sin 2t |
|
|
|
. |
|
|
|
||||||||
|
2 |
|
0 |
4 |
0 |
|
4 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Приближенное вычисление определенных интегралов |
|||||||||||||||||||||
1. Формула прямоугольников |
|
|
|
|
|
x x |
|
|
|
||||||||||||
b |
|
|
|
|
|
b a N 1 |
|
|
|||||||||||||
f x |
dx |
|
|
|
|
f |
k |
|
|
k 1 |
, |
|
|||||||||
|
|
N |
|
|
|
2 |
|
|
|||||||||||||
a |
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
||||||
где x k – точки разбиения отрезка |
a,b , N – число частичных отрезков. |
||||||||||||||||||||
95

Остаточный член квадратурной формулы (ошибка)
|
|
M1 |
b a 2 |
|
|
||||
R |
|
|
, |
|
|
|
|||
n |
|
|
4N |
|
|
|
|
||
где f x M1 x a,b .
2. Формула трапеций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
b |
b a |
f |
|
x |
0 |
|
f |
|
x |
|
|
f |
|
x |
N 1 |
f |
|
x |
N |
|
|
|
f x dx |
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||
N |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
b a f x0 2 f x1 2 f x2 2 f xN 1 f xN . N
|
|
|
|
|
M1 b a 2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
R |
|
|
|
. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
N |
|
4N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x |
|
M2 |
|
|
Если f(x) имеет ограниченную вторую производную |
|
|
на |
|||||||||||
|
|
|||||||||||||
[a,b], то для формул трапеций и прямоугольников |
|
|
|
|
|
|
||||||||
|
|
|
|
|
M2 b a 3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
R |
N |
|
|
. |
|
|
|
|
|
|
||
|
|
12N 2 |
|
|
|
|
|
|
|
|||||
3.Формула Симпсона |
|
|
y f x |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
Если |
заменим график |
функции |
на каждом отрезке |
|||||||||||
xi 1, xi |
не отрезками прямых, как в |
методах |
прямоугольников |
и |
||||||||||
трапеций, а дугами парабол, то получим более точную формулу для приближенного вычисления интеграла:
b f x dx |
h |
y0 y2m |
2 y2 y4 y2m 2 4 y1 y3 |
y2m 1 |
|
, |
|
||||||
|
3 |
|
|
|
|
|
a |
|
|
|
|
|
|
h b a . 2m
Приложения определенных интегралов
1.Вычисление площадей плоских фигур
1.1.Площадь фигуры, заданной в декартовых координатах.
Пусть y=f(x) – уравнение линии, ограничивающей трапецию сверху.
96
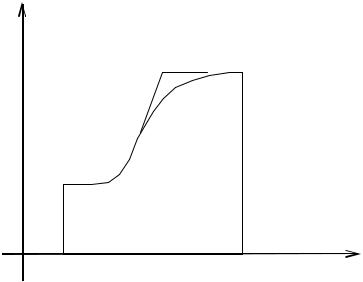
y
L:y=f(x) В
|
А |
|
|
|
|
|
|
|
S |
|
|
||
|
|
|
|
|
|
|
|
a |
|
|
b |
x |
|
|
|
|
||||
Если y 0 , то |
|
|
|
|
|
|
|
|
|
b |
|
||
|
S f x dx. |
|
||||
|
|
|
a |
|
||
1.2. Площадь фигуры при задании линии L в параметрической |
||||||
форме |
|
|
|
|
|
|
|
L : |
x x t , |
|
|||
|
y y t . |
|
||||
b |
|
x x t ; dx x t dt |
|
|||
|
|
|||||
|
|
|
|
|
|
|
S y x dx |
x a t t1 |
|
||||
a |
|
x b t t2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
S y t x t dt. |
|
||||
|
|
t1 |
|
|
|
|
2. Вычисление объемов тел по площадям параллельных сечений
Если тело T расположено между x a и x b , а непрерывная функция S(x) C закон изменения площади его поперечного сечения, то объем V этого тела
b
V S x dx.
a
97

Объем тела вращения
|
b |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
V |
|
x |
|
|
|
x |
|
|
|
|
|
||||||
|
f |
|
2 dx |
|
f |
|
2 dx. |
|
|
|
|||||||
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
3. Вычисление длины дуги кривой |
|
||||||||||||||||
Если кривая задана в виде |
y f x , где |
f x |
|
– непрерывная и |
|||||||||||||
имеет непрерывную производную f x |
на отрезке a,b , то длина дуги |
||||||||||||||||
этой кривой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
1 y 2 dx. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
x |
x |
|
t |
|
, |
|
Если кривая задана параметрически в виде |
y t |
|
t1 t t2 , то |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
t y 2 t dt. |
|
|
|
|
|
||||||
|
|
L |
|
x 2 |
|
|
|
|
|
||||||||
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Площадь поверхности вращения |
|||||||||||||||||
Если поверхность |
определяется |
|
вращением |
|
кривой y f x |
||||||||||||
( a x b ) вокруг оси Ox, где f x |
и f x |
– непрерывны, то площадь |
|||||||||||||||
указанной поверхности вращения: |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P 2 f x |
|
1 f 2 x dx. |
|
|
|
|
||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Физические приложения определенных интегралов |
|||||||||||||||||
5.1. Центр тяжести |
C xc , yc |
|
однородной |
пластины постоянной |
|||||||||||||
толщины с поверхностной плотностью const , ограниченная кривой
y f x и прямыми y 0 , x a, |
x b определится в виде: |
|||||||||
|
|
|
b |
|
|
|
1 |
b |
|
|
|
|
|
xf x dx |
|
|
f 2 |
x dx |
|||
|
|
|
; y |
2 |
||||||
x |
c |
a |
|
|
a |
|
. |
|||
b |
|
|
b |
|
||||||
|
|
|
c |
|
|
|||||
|
|
|
f x dx |
|
|
|
|
f x dx |
||
|
|
|
a |
|
|
|
|
a |
|
|
98
5.2. Работа переменной силы X f x , действующей в направлеC нии оси Ox при прямолинейном перемещении на отрезке x0 , x1 выC
числяется по формуле
x1
A f x dx .
x0
5.3. Путь, пройденный точкой со скоростью v t :
|
|
n 1 |
t |
S |
lim |
v k tk |
v t dt. |
|
max tk 0 |
k 0 |
0 |
|
|
Несобственные интегралы
1. Несобственные интегралы с бесконечными пределами (несоб3 ственный интеграл I рода)
Несобственный интеграл f x dx от функции f(x), интегрируемой на
a
любом отрезке [a,b ], a b , определяется в виде
|
|
|
|
|
b |
|
|
|
|
|
|
f |
x |
b |
f |
x |
dx. |
||||
|
|
|
dx lim |
|
|
|||||
a |
|
|
|
|
a |
|
|
|
|
|
Аналогично определяется несобственный интеграл на интервале (– ,b]:
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
f |
x |
dx lim |
|
|
f |
x |
dx. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|||
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 dx |
|
1 |
|
dx |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
lim |
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
lim |
|
1 |
|
|
1. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
2 |
|
a |
|
|
2 |
|
a |
|
|
|
|
|
|
|
|
a |
|
|
|
|||||||||||
|
x |
|
|
a x |
|
|
|
|
|
|
|
|
x |
|
a |
|
|
|
|
|
|
|
a |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2. Интеграл от разрывной функции |
|
||||||||||||||||||||||||||
|
|
|
|
(несобственный интеграл II рода) |
|
||||||||||||||||||||||||||
Если непрерывная на промежутке |
|
|
|
|
функция f(x) имеет бескоC |
||||||||||||||||||||||||||
|
a,b |
|
|||||||||||||||||||||||||||||
нечный разрыв при x b и если существует конечный предел |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
f |
x |
dx, 0 , |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
a
то его называют несобственным интегралом второго рода и обозначают
b
f x dx . Если предел существует, то несобственный интеграл
a
99

b
f x dx называется сходящимся, если предел не существует или бесC
a
b
конечен, то интеграл f x dx расходится.
a
Аналогично определяется несобственный интеграл, когда f(x) терC пит разрыв в точке а:
|
b |
|
|
|
|
0 |
b |
|
|
|
|
|
|
|
f |
x |
|
f |
x |
dx. |
|||||
|
|
|
|
dx lim |
|
|
|
|||||
|
a |
|
|
|
|
|
a |
|
|
|
|
|
Если f x |
терпит разрыв во внутренней точке c отрезка a,b , то |
|||||||||||
несобственный интеграл второго рода определяется формулой:
b |
c |
b |
f x dx f x dx f x dx . |
||
a |
a |
c |
Интеграл слева называют сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.
Примеры.
|
a |
dx |
|
|
a |
|
dx |
|
|
|
|
|
|
|
|
a |
lim 2 a 2 |
|
2 a. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1. |
|
|
|
lim |
|
|
|
|
lim 2 |
|
x |
|
|
|
|||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
x |
|
0 |
|
x |
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
dx |
|
lim b |
dx |
lim |
|
ln |
|
|
|
|
|
b |
lim |
|
ln |
|
b |
|
ln1 |
lim ln b ; |
|||||||
|
|
|
|
x |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
x |
|
b |
|
x |
b |
|
|
|
|
|
|
1 |
|
b |
|
|
|
|
|
|
|
b |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интеграл расходится.
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
x |
|
|
|
1 |
, 1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3. |
|
dx |
lim |
dx |
lim |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|||||||||||||||||||||||
|
x |
0 |
|
x |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, 1 |
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
ln1 ln , 1 |
|
|
|
|
|
|
|
|
ln , 1 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
0 |
|
|
1 |
|
|
|
|
|
|
, |
1 |
0 |
|
|
|
1 1 , 1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ln , 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, 1 расходится, |
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
lim |
|
|
|
|
1 |
|
|
|
, 1 |
, |
1 расходится, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|||||||||||||||||||||||
|
|
|
|
0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
1 1 , |
1 |
|
|
|
, 1 |
сходится. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1C |
|
|
|
|||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
100
