1545

11. Материальная точка совершает гармонические колебания согласно

2) период колебаний; 3) начальную фазу колебаний; 4) максимальную скорость точки; 5) максимальное ускорение точки; 6) через сколько времени после начала отсчета точка будет проходить через положение равновесия.

О т в е т: 1) A 2 см; 2) T 2 с; 3) 2 ; 4) max 6,28 см/с; 5) amax 19,7 см/c 2 ; 6) t m с, где m 0, 1, 2, 3, …

12. Материальная точка, совершающая гармонические колебания с частотой v 1 Гц, в момент времени t 0 проходит положение, определяемое координатой x0 5 см, со скоростью 0 15 см/с. Определите

амплитуду колебаний. О т в е т: A 5,54 см.

13. Начальная фаза колебаний точки равна 0 3 . Период колебаний T 0,06 с. Определитe ближайшие моменты времени, в которые скорость

иускорение в два раза меньше амплитудных значений.

От в е т: t1 0; t2 0,025c.

14. Точка совершает гармонические колебания. В некоторый момент времени смещение точки x 5 см, скорость = 20 см/с и ускорение а 80 cм/c2. Определите: циклическую частоту, период, амплитуду и фазу колебаний в этот момент времени.

О т в е т: 0 4с -1; Т 1,57 с; А 7,07 см; 0 4 рад.

15. Частица массой 5 г совершает гармонические колебания по закону х Аsin 2 t , где А 3 см; 0,5 Гц. Определите максимальную силу, действующую на частицу.

О т в е т: F 1,5 мН.

16. Тело массой m 10 г совершает гармонические колебания по закону x 0,1cos 4 t 4 , м. Определите максимальные значения: 1) воз-

вращающей силы; 2) кинетической энергии.

О т в е т: 1) Fmax 0,158 Н; 2) Tmax 7,89 мДж.

21

17. Материальная точка массой m 50 г совершает гармонические колебания согласно уравнению x 0,1cos 32 t , м. Определите: 1) возвраща-

ющую силу F для момента времени t 0,5 с; 2) полную энергию E точки.

О т в е т: 1) F 78,5 мН; 2) E 5,55 мДж.

18. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой A 6 см. Определите полную энергию E колебаний груза, если жесткость k пружины составляет 500 Н/м.

О т в е т: E kA22 0,9 Дж.

19. Материальная точка массой m 20 г совершает гармонические колебанияпо закону x 0,1cos 4 t 4 , м. Определитеполнуюэнергию E этой

точки.

О т в е т: E 15,8 мДж.

20. Полная механическая энергия частицы, колеблющейся по синусоидальному закону, равна 30 мкДж, а максимальная сила, действующая на неё, равна 1,5 мН. Запишите уравнение колебаний точки, если период колебаний 2 с, а начальная фаза 3.

От в е т: x 0,04cos t .

3

хх0 sin 2 t . В какой момент времени ее потенциальная энергия рав-

6

на кинетической?

23. Материальная точка массой 10 г колеблется по закону х 0,05sin 0,6t 0,8 . Определите максимальную силу, действующую на

точку, и полную энергию колебаний.

О т в е т: Fmax 1,8 10 4 H; W 4,5 мкДж.

22

24. Точка совершает гармонически колебания, уравнение которых имеет вид х 0,05sin 2t. Определите момент времени (ближайший к нача-

лу отсчета), в который потенциальная энергия точки П=10–4 Дж, а возвра-

щающая сила F 5 10 3 Н. Какова фаза колебаний в этот момент времени?

О т в е т: t 2,04 с; 4,07 рад.

25. Материальная точка колеблется согласно уравнению x Acos t , где A 5 см и 12 с 1 . Когда возвращающая F сила в первый раз

достигает значения –12 мН, потенциальная энергия П точки оказывается равной 0,15 мДж. Определите: 1) этот момент времени t ; 2) соответствующую этому моменту фазу t .

О т в е т: 1) t 4 с; 2) t 3 рад.

26. Амплитуда колебаний груза массой 1,5 кг, скрепленного с горизонтальной пружиной, жесткость которой 1200 Н/м, равна 0,1 м. Определите кинетическую и потенциальную энергию системы при фазе 50°, ее полную механическую энергию и период колебаний.

О т в е т: Т 4,5 Дж; П=1,5 Дж; Е 6 Дж; t 0,22 с.

1.3. Гармонический осциллятор

Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида

d 2s 2s 0 . dt2 0

Колебания гармонического осциллятора являются важным примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются пружинный, физический и математический маятники.

1.3.1. Пружинный маятник

Пружинный маятник – система, состоящая из груза массой m , прикрепленного к абсолютно упругой пружине, и совершающая гармониче-

ские колебания под действием упругой силы F kx , где k жесткость пружины, x смещение груза от положения равновесия в момент времени t

(рис.4).

23

На основании второго закона

Ньютона F ma , или F m d 2 x . dt2

Отсюда следует

Выражение (15) является дифференциальным уравнением свободных незатухающих колебаний пружинного маятника.

Величина 0 k m является ци-

клической частотой колебаний пружин- Рис. 4 ного маятника. Учитывая это, формулу

(15) можно записать в виде

d 2 x k x 0 . dt2 m

Решением этого однородного дифференциального уравнения второго порядка является функция вида

x Asin( 0t 0 ) ,

где A и 0 – произвольные постоянные, для определения которых необхо-

димо знать начальные условия. Каждое конкретное колебание характеризуется определенными значениями амплитуды A и начальной фазы 0 .

Тело данной массы m, находясь под действием одной и той же упругой силы F kx , может совершать колебания с различными амплитудами и начальными фазами в зависимости от начальных условий, но период колебания всегда остается одним и тем же.

Период колебаний пружинного маятника

T 2 mk .

1.3.2. Физический маятник

Физический маятник – твердое тело, совершающее под действием силы тяжести колебания около неподвижной горизонтальной оси O , не проходящей через центр масс C тела (рис. 5).

На рис. 5 F и Fn тангенциальная и нормальная составляющие силы тяжести mg . При отклонении маятника от положения равновесия на угол

24

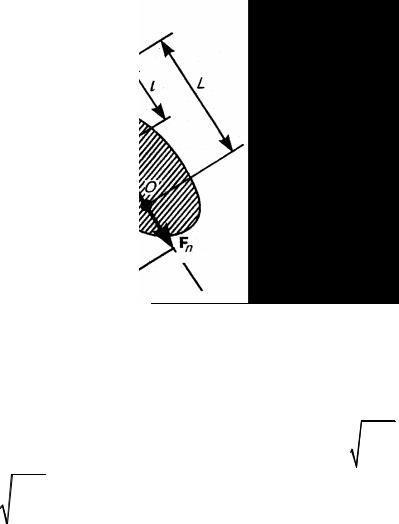
тангенциальная составляющая F возвращает его к положению равновесия.

F mg sin .

При малых sin , поэтому F mg . Вращающий момент этой силы

где m масса маятника; l расстояние от точки подвеса O до центра масс

Cмаятника.

Всоответствии с основным законом динамики вращательного движения

где J момент инерции маятника относительно оси вращения.

Из (16) и (17) следует:

Выражение (18) является дифференциальным уравнением свободных незатухающихколебанийфизическогомаятника.

Решением этого уравнения является Рис. 5 функция вида

1.3.3. Математический маятник

Математический маятник – идеализированная система, состоящая из материальной точки массой m , подвешенной на нерастяжимой невесомой нити, колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой нити (рис. 6).

25

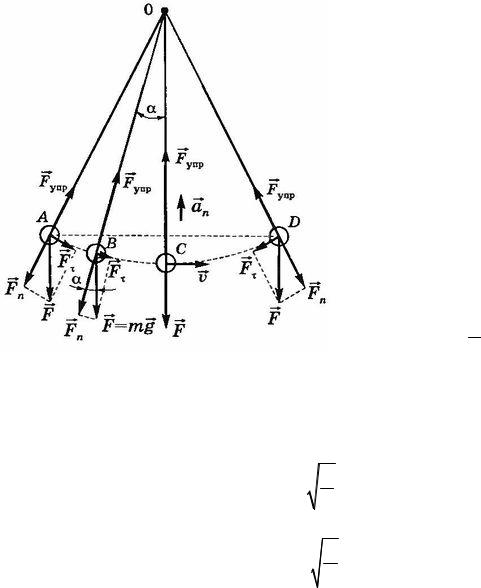
Колебания математического маятника, как и физического, происходят под действием тангенциальной составляющей силы тяжести.

Момент инерции материальной точки относительно точки подвеса

J ml2 ,

поэтому дифференциальное уравнение свободных незатухающих колебаний математического маятника имеет вид

d 2 2 g 0, dt l

Отсюда следует, что математический маятник совершает гармонические колебания по закону 0 sin( 0t 0 ) с циклической частотой

0 gl

и периодом

T 2 gl .

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. Математический маятник длиной l1 40 см и физический маятник в виде тонкого прямого стержня длиной l2 60 см синхронно

колеблются около одной и той же горизонтальной оси. Определите расстояние центра масс стержня от оси колебаний.

26

Период колебаний математического маятника

Период колебаний математического маятника

T2 2 mgaI ,

где I 121 ml22 ma2 m 121 l22 a2 .

Тогда

Приравняем выражения для периодов колебаний маятников

Выразим из полученной формулы l1

l2 12a2 l1 2 12a

и приведем это уравнение к виду

12a2 12l1a l22 0 .

Это квадратное уравнение имеет два решения: a1 0,3 м; a2 0,1 м. Если a1 0,3 м, то центр масс стержня находится на краю стержня,

следовательно, этот ответ неверный.

О т в е т: a 0,1 м.

Пример 2. Брусок массой M 10 кг, лежащий на гладкой горизонтальной поверхности, прикреплён к горизонтальной пружине жёсткости k . В брусок попадает и застревает в нём пуля массой m 9 г, летящая со скоростью 500 м/с, направленной вдоль оси пружины. Амплитуда возникших при этом колебаний A 0,1 м. Определите период этих колебаний.

27

где u скорость бруска и застрявшей в нём после взаимодействия пули.

Согласно закону сохранения энергии

где k – жёсткость пружины.

Из уравнений (1) и (2) следует, что

Циклическая частота возникших гармонических колебаний

Период колебаний равен

T 2 A(Mm m) .

О т в е т: T =14 с.

Пример 3. Деревянный брусок массой m 3,2 кг с площадью основания S 400 см2 плавает в воде. Брусок слегка погрузили в воду глубже и отпустили. Найдите частоту колебаний бруска. Силой трения пренебречь. Плотность воды 1000 кг/м3.

28

Спроектируем это уравнение на вертикально направленную ось X :

где V1 объем погруженной части бруска.

Если глубину погружения бруска увеличить на x , то сила Архимеда станет равной

FA g V1 xS .

Подставив в формулу (2) значение силы тяжести из (1), получим

Fx gSx ,

то есть на брусок будет действовать сила, пропорциональная смещению его из положения равновесия, и уравнение движения бруска примет вид

a mgS x 0 .

Следовательно, собственная циклическая частота колебаний бруска будет равна

О т в е т: 1,8 Гц.

Пример 4. Шарик подвешен на длинной нити. Первый раз его поднимают по вертикали до точки подвеса, второй раз отклоняют на небольшой угол. В каком из этих случаев шарик быстрее возвращается к начальному положению, если его отпустить?

29

рика с высоты, равной длине l нити:

ния в положение равновесия найдем из уравнения гармонических колебаний x Asin 0t 0 . Так как в начальный момент времени маятник

имеет максимальное отклонение от положения равновесия, то 0 2. Поскольку в положении равновесия x 0 , то 0 Asin 0t2 2 , сле-

довательно, sin t2 2 0, t2 2 , откуда

Шарик представляет собой математический маятник, поэтому период его колебаний T 2 l g . Подставив это выражение в (2), найдем

Следовательно, в первом случае шарик быстрее возвратится к начальному положению.

О т в е т: в первом случае

Пример 5. Физический маятник представляет собой тонкий однородный стержень длиной 35 см. Определите, на каком расстоянии от центра масс должна быть точка подвеса, чтобы частота колебаний была

30