1540

BUILDING STRUCTURES, BUILDINGS AND CONSTRUCTIONS

При решении практических задач по расчёту тонких жёстких пластинок, нагруженных поверхностными нормальными и касательными нагрузками, следует иметь в виду, что внешний вид эпюр внутренних усилий в поперечных сечениях пластинки может сориентировать пользователя и показать наиболее нагруженные зоны в пластинке. При этом прочность пластинки в точке необходимо будет определять в соответствии с теориями прочности (Треска – Сен-Венана, Губера – Мизеса – Генки и так далее) для трёхмерного напряжённого состояния, то есть в соответствии с напряжениями, определяемыми формулами (71), (72), (74), (8) и (9).

Вопросы формирования статических и геометрических условий на контуре тонкой жёсткой пластинки, находящейся под действием нормальных и касательных поверхностных нагрузок, определяются условиями закрепления и в данной работе не рассматриваются. Что же касается приведённых поперечных сил и реакций в углах прямоугольной пластинки, то формулы Максвелла

остаются справедливыми и в данном случае, однако, принимая во внимание формулы

(12) и (16), получаем:

Сосредоточенные реакции в углах прямоугольной пластинки будут определяться по формулам

З а м е ч а н и е . Если интенсивность касательных нагрузок остаётся постоянной, то дифференциальное уравнение изогнутой срединной поверхности тонкой жёсткой пластинки с касательными нагрузками будет таким же, как и для пластинок, нагруженных только поперечной нагрузкой, и, следовательно, прогибы у пластинки с касательными нагрузками будут такими же, как и у пластинок, нагруженных только поперечной нагрузкой.

Пример расчёта. Рассмотрим тонкую жёсткую пластинку, шарнирно опёртую по всем четырём сторонам [15, §4.4] (рис. 5). В работе [15] расчёт пластинки, нагруженной равномерно распределённой нормальной нагрузкой интенсивностью q

по всей площади, выполнялся методом конечных разностей.

При этом напряжения в центральном сечении пластинки при x 2l и y 2l на срединной плоскости при z 0 определялись соотношениями:

x y xy xz yz 0 .

СТРОИТЕЛЬНЫЕ КОНСТРУКЦИИ, ЗДАНИЯ И СООРУЖЕНИЯ

X

l

q

l

Y

Рис. 5. Пластинка, шарнирно опёртая по контуру

xy 0; zx 0; zy 0.

Рассмотрим случай, когда на пластинку кроме нормальной действуют ещё и касательные нагрузки tx и ty , равномерно распределённые по всей площади

пластинки. При этом напряжения в центральном сечении пластинки при x 2l и

y 2l на срединной плоскости при z 0 будут определяться зависимостями:

x y xy 0; xz 32 tx ; yz 32 ty .

На поверхности пластины при z h2 напряжения будут равны:

Заключение и выводы. Сформулированы гипотезы для расчёта тонких жёстких пластинок, нагруженных не только нормальной, но и касательными нагрузками по верхней стороне пластинки.

Получены выражения и для деформаций, и для напряжений, и для внутренних усилий, действующих в поперечных сечениях пластинки.

Построено уравнение изогнутой срединной поверхности пластинки. Дифференциальное уравнение изогнутой срединной поверхности тонкой жёсткой пластинки, нагруженной нормальными и касательными нагрузками, отличается от уравнения Софи-Жермен – Лагранжа лишь изменённой правой частью.

Полученные соотношения могут найти применение при расчёте тонких жёстких пластинок, нагруженных как нормальными, так и касательными нагрузками.

BUILDING STRUCTURES, BUILDINGS AND CONSTRUCTIONS

Список литературы

1.Reissner, E. On the theory of bending of elastic plates / E. Reissner // J. of Math, and Phys. – 1944. – № 23. – Р.184–191.

2.Reissner, E. The effect of transverse shear deformation on the bending» of elastic plates / E. Reissner // J. Appl. Mech. – 1945. – Vol. 12, 1.

3. Во11e, L. Contribution on probleme lineaire de flexion d'une plaque elastique / L. Во11e // Bull. Technique de la Suisse Romande. – 1947. – Vol. 73. – Р. 281–285, 293– 298.

4.Chi-Teh. Wan. Principle and application of complementary energy method for thin homogeneous and sandwich plates and shells with finite deflections / Chi-Teh Wan // NACA TN 2620. – 1952.

5.Schafer, W.M. Uber eine Verfeinerung der Klassischen Theorie dunner schwach gebogener Platten / W.M. Schafer // ZAMM. – 1952. – №32. – Р.161–171.

6.Frederick, D. On some problems in the bending of thick circular plates on a elastic foundation / D. Frederick // J. Appl. Mech. – 1956. – Vol. 23. – Р. 2.

7.Гольденвейзер, А.Л. О теории изгиба пластинок Рейсснера / А.Л. Гольденвейзер // Изв. АН СССР ОТН. – 1958. – № 4.

8.Кое11er, R.С. Shear deformation in rectangular plates / R.С. Кое11er, F. Еssenburg // Proc. 4th U. S. Congr. Appl. Mech. – 1962. – Vol. 1.

9.Rudiger, D. Eingespannte Rechteckplatten mit Schubverzerrungen / D. Rudiger // ZAMM. – 1963. – № 43. – Р. 1–2.

10.Айнола, Л.Я. Об уточненных теориях пластинок типа Рейсснера. Теория оболочек и пластин / Л.Я. Айнола. – Ереван, 1964.

11.Розе, А.В. К изгибу пластин из ориентированных стеклопластиков / А.В. Розе // Механика полимеров. – 1965. – № 3.

12.Гаврилов, Т.А. Ориентированная стружечная плита при действии поверхностной касательной нагрузки / Т.А. Гаврилов, Г.Н. Колесников // Вопросы теории и практики инновационного развития науки и образования / отв. ред. Г.Ю. Гуляев. –

Пенза, 2018. – С. 163–171.

13.Александрова, Н.П. Особенности расчета асфальтобетонных покрытий по сопротивлению сдвигу с учетом накапливания повреждений / Н.П. Александрова, В.В. Чусов // Вестник Сибирской государственной автомобильно-дорожной академии. – 2016. – № 3 (49). – С. 42–50.

14.Тимошенко, С.П. Пластинки и оболочки / С.П. Тимошенко, С. ВойновскийКригер. – М.: Физматгиз, 1963.

15.Бакушев, С.В. Численные методы решения задач механики деформируемого твёрдого тела / С.В. Бакушев. – М.: ЛЕНАНД, 2021. – 426 с.

References

1.Reissner, E. On the theory of bending of elastic plates / E. Reissner // J. of Math, and Phys. – 1944. – № 23. – Р.184–191.

2.Reissner, E. The effect of transverse shear deformation on the bending» of elastic plates / E. Reissner // J. Appl. Mech. – 1945. – Vol. 12, 1.

3. Воlle, L. Contribution on probleme lineaire de flexion d'une plaque elastique / L. Воlle // Bull. Technique de la Suisse Romande. – 1947. – Vol. 73. – Р. 281–285, 293– 298.

4.Chi-Teh. Wan. Principle and application of complementary energy method for thin homogeneous and sandwich plates and shells with finite deflections / Chi-Teh Wan // NACA TN 2620. – 1952.

5.Schafer, W.M. Uber eine Verfeinerung der Klassischen Theorie dunner schwach gebogener Platten / W.M. Schafer // ZAMM. – 1952. – №32. – Р.161–171.

6.Frederick, D. On some problems in the bending of thick circular plates on a elastic foundation / D. Frederick // J. Appl. Mech. – 1956. – Vol. 23. – Р. 2.

СТРОИТЕЛЬНЫЕ КОНСТРУКЦИИ, ЗДАНИЯ И СООРУЖЕНИЯ

7.Goldenweiser, A.L. On the theory of bending of Reissner plates / A.L. Goldenweiser // Izv. AN USSR REL. – 1958. – No. 4.

8.Кое11er, R.С. Shear deformation in rectangular plates / R.С. Кое11er, F. Еssenburg // Proc. 4th U. S. Congr. Appl. Mech. – 1962. – Vol. 1.

9.Rudiger, D. Eingespannte Rechteckplatten mit Schubverzerrungen / D. Rudiger // ZAMM. – 1963. – № 43. – Р. 1–2.

10.Ainola, L.Ya. About improved theories of Reissner-type plates. The theory of shells and plates / L.Ya. Ainola. – Yerevan, 1964.

11.Roze, A.V. To the bending of oriented fiberglass plates / A.V. Roze // Mechanics of polymers. – 1965. – No. 3.

12.Gavrilov, T.A. Oriented strand board under the action of tangential surface loads / T.A. Gavrilov, G.N. Kolesnikov // Theory and practice issues of science and education innovative development. – Penza, 2018. – Р. 163–171.

13.Alexandrova, N.P. Calculation of asphalt concrete pavements on shear strength taking into account the accumulation of microdamage / N.P. Alexandrova, V.V. Chusov // Bulletin of Siberian State Automobile and Highway Academy. – 2016. – No. 3 (49). – Р. 42– 50.

14.Timoshenko, S.P. Plates and shells / S.P. Timoshenko, S. Voinovsky-Krieger. – М.: Fizmatgiz, 1963.

15.Bakushev, S.V. Numerical methods for solving problems of solid mechanics / S.V. Bakushev.– M.: LENAND, 2021. – 426 p.

ENGINEERING SYSTEMS

ИНЖЕНЕРНЫЕ СИСТЕМЫ

ENGINEERING SYSTEMS

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАСПРЕДЕЛЕНИЯ КОНВЕКТИВНОГО ПОТОКА НАД КОМПАКТНО РАСПОЛОЖЕННЫМИ ТОЧЕЧНЫМИ ТЕПЛОВЫМИ ИСТОЧНИКАМИ

В.В. Кузина, А.Н. Кошев, А.И. Еремкин

Рассматривается задача математического моделирования аэродинамических процессов, происходящих в результате формирования конвективного потока над ограниченным множеством компактно расположенных точечных тепловых источников.

Ключевыеслова: конвективныйпоток, тепловойисточник, математическоемоделирование

MATHEMATICAL MODELING OF DISTRIBUTION OF CONVECTIVE FLOW OVER A LIMITED SET OF COMPACT POINT HEAT SOURCES

V.V. Kuzina, A. N. Koshev, A.I. Eremkin

The problem of mathematical modeling of aerodynamic processes occurring as a result of the formation of a convective flow over a limited set of compactly located point heat sources is considered

Keywords: convective flow, heat source, mathematical modeling

ИНЖЕНЕРНЫЕ СИСТЕМЫ

Проблема отведения тепла от компактно расположенных тепловых источников встречается при решении различных задач теплофизики, теплоснабжения и вентиляции [1-3]. Например, актуальной является задача теплоотведения от элементов бытовых и электронных приборов, нагревателей, осветительных приборов и пр. в процессе их эксплуатации, для решения которой чаще всего используется вынужденная конвекция. Однако для решения задачи обеспечения вынужденной конвекции и вентиляции воздуха необходимы знания о распределении и интенсивности тепловых потоков и геометрии так называемых плюмов – тепловых течений, образующихся в условиях постоянного действия источника тепла [4].

В данной работе мы будем рассматривать тепловые потоки от точечных тепловых источников, расположенных на круге симметрично его центру (рис. 1, а). Над каждым источником возникает конвективный поток заданной мощности, который схематично изображен на рис. 1, б.

Согласно теории, тепловые потоки от точечных тепловых источников имеют круговуюсимметриюотносительновертикальнойосииобычноназываютсякомпактными[5].

Примем следующие обозначения: z, r – цилиндрические координаты. Приращение импульса конвективного потока, равное подъемной силе, дей-

ствующей на нагретый воздух на уровнях z и z dz :

Количество тепла, проводимое нагретым воздухом через поперечное сечение потока, равное конвективной теплопроводности источника:

z

x r

Рис. 1. Схематичное изображение точечных тепловых источников (а) и создаваемых ими конвективных потоков (б)

Распределение скорости: w – в поперечном сечении (z = const) в произвольной точке, wz – на оси z конвективного потока:

ENGINEERING SYSTEMS

Избыточные температуры воздуха: v – в поперечном сечении (z = const) в произвольной точке, vz – на оси z конвективного потока:

В уравнениях (3), (4) с и σ – некоторые экспериментально найденные константы. В [1, с. 76] приводятся с = 0,082; σ = 0,8.

Вуравнениях (5), (6) Т, Тz, Т∞ – абсолютные температуры воздуха, соответственно,

впроизвольной точке сечения, на оси z и в окружающей среде.

С использованием естественных допущений, а также ряда преобразований получены уравнения [5, с. 75–78] для вертикальной составляющей скорости движения и избыточной температуры воздуха в любой точке пространства:

В уравнениях (7), (8): ρ∞ – плотность воздуха вне потока; cp – теплоемкость воздуха при постоянном давлении.

На основании уравнений (7), (8) с использованием естественных предположений

(1) – (4), а также несложных преобразований и допущений получены уравнения [5, с. 81–87] для расчета скорости движения воздуха и избыточной температуры воздуха в произвольной точке сложного конвективного потока, образованного двумя одинаковыми тепловыми источниками, расположенными на одинаковом уровне и на одинаковом расстоянии от центра координат (примерно, как на рис. 2).

В приведенных уравнениях величина a – расстояние от начала координат до

источника (считается одинаковой для каждого источника).

При выводе формул (9) – (10) принято естественное предположение, что в силу симметрии взаимное перетекание воздуха из частей пространства, занятых воздухом каждого из источников, невозможно. Кроме того, принято известное положение, что при взаимодействии конвективных потоков можно использовать правила сложения кубов скоростей.

ИНЖЕНЕРНЫЕ СИСТЕМЫ z

y P(x,y)

Рис. 2. Схематичное изображение сложного конвективного потока, образованного двумя одинаковыми тепловыми источниками, расположенными на одинаковом уровне и на одинаковом расстоянии от центра координат

Эти же предположения и положения будем использовать и при расчете взаимодействия n конвективных потоков, расположенных симметрично относительно центра некоторого круга (рис. 3).

P(xi,yi)

xi

y

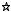x

T(x,y)

Рис. 3. Схематичное изображение n конвективных потоков, расположенных симметрично относительно центра некоторого круга

ENGINEERING SYSTEMS

На рис. 3 – верхний конец источника (например свечи). Общее количество

источников n – Pi(xi, yi), i =1,..., n; T(x, y) – произвольная точка на круглой подставке; Ri – расстояние от точки T до точки Pi.

выражения для скоростей конвективного потока, продуцированного i-м тепловым источником (i-й свечой) wi:

По правилу сложения кубов скоростей независимых конвективных потоков, скорость движения воздуха в произвольной точке сложного конвективного потока выражается формулой

Теперь можно записать общее уравнение для плотности сложного теплового потока в произвольной точке T(x, y):

Использование уравнений (12), (13) при конкретных заданных параметрах тепловых источников позволило определить:

координаты z – значения zmax(w) и zmax(v), соответствующие максимальной скорости и максимальной плотности теплового потока;

значения wmax и v max в сложном конвективном потоке;

значение Rmax в плоскостях z = zmax(w) и z = zmax(v),

атакже исследовать функцию R = R(w), т.е. форму теплового потока.

Список литературы

1.Cheikh, N.B. Influence of thermal boundary conditions on natural convection in a square enclosure partially heated from below / N.B. Cheikh, B.B. Beya, T. Lili // International communications in heat and mass transfer. – 2007. – Vol. 34, № 3. – Р. 369–379.

2.Kuznetsov, G.V. Conjugate natural convection in an enclosure with local heat sources / G.V. Kuznetsov, M. Sheremet // Computational Thermal Sciences: An International Journal. – 2009. – Vol. 1, № 3. – P. 341–360.

3.Sezai, I. Natural convection from a discrete heat source on the bottom of a horizontal enclosure / I. Sezai, A. Mohamad // International Journal of Heat and Mass Transfer. – 2000. – Vol. 43, № 13. – С. 2257–2266.

4.Turner, J. Buoyant plumes and thermals / J. Turner // Annual Review of Fluid Mechanics. – 1969. – Vol. 1, № 1. – P. 29–44.

5. Шепелев, И.А. Аэродинамика воздушных потоков в помещении / И.А. Шепелев. – М.: Стройиздат, 1978. – 144 с.

References

1. Cheikh, N.B. Influence of thermal boundary conditions on natural convection in a square enclosure partially heated from below / N.B. Cheikh, B.B. Beya, T. Lili // International communications in heat and mass transfer. – 2007. – Vol. 34, № 3. – Р. 369–379.

ИНЖЕНЕРНЫЕ СИСТЕМЫ

2.Kuznetsov, G.V. Conjugate natural convection in an enclosure with local heat sources / G.V. Kuznetsov, M. Sheremet // Computational Thermal Sciences: An International Journal. – 2009. – Vol. 1, № 3. – P. 341–360.

3.Sezai, I. Natural convection from a discrete heat source on the bottom of a horizontal enclosure / I. Sezai, A. Mohamad // International Journal of Heat and Mass Transfer. – 2000. – Vol. 43, № 13. – С. 2257–2266.

4.Turner, J. Buoyant plumes and thermals / J. Turner // Annual Review of Fluid Mechanics. – 1969. – Vol. 1, № 1. – P. 29–44.

5.Shepelev, I.A. Aerodynamics of air flows in a room / I.А. Shepelev. – M.: Stroyizdat, 1978. – 144 р.