
1532
.pdf
START HOLD END |
7 |
8 |
9 |
m ↔ft |
AVER |
4 |
5 |
6 |
UNIT |
OFF |
1 |
2 |
3 |
SCALE |
ON/ C |
0 |
· |
D-SCL |
SF? |
Рис.19. Функциональные клавиши:
START – готовность к началу измерений. На экране дисплея отображается «0»; HOLD – удержание в памяти площади измеренной фигуры. При повторном нажатии клавиши HOLD можно продолжить измерение. С помощью этой клавиши производится накопление измерений; END – используется
для неоднократного измерения одной и той же площади; AVER – каждое измерение сохраняется нажатием клавиши END и усредняется нажатием клавиши AVER; ON/C – включение питания (очистка памяти);
OFF – выключение питания; 0–9 – цифровые клавиши; (м ↔ ft) – выбор метрической или английской системы единиц; UNIT – отображение выбранных единиц измерений; см², м², км² в метрической системе измерений, и квадратных дюймов, квадратных футов и акров в Английской системе измерений; SCALE – клавиша ввода масштаба; D – SCL – клавиша ввода двойного масштаба; SF? – запрос масштабного коэффициента
При определении площади планиметром PLANIX 7 рекомендуется производить ее измерение не менее трех раз, так как площадь, вычисленная как среднее из нескольких замеров, наиболее приближена к истинному значению. Для этого после каждого измерения площади необходимо нажимать клавишу END, а после окончания измерений – клавишу AVER. В результате получаем среднее значение площади из нескольких замеров. Например: средняя величина площади четырехугольного полигона 1–2–3–4, полученная из трех замеров планиметром PLANIX 7, равна 520500 м2 или 52,05 га. Более подробно порядок работы с планиметром PLANIX 7 описан
вмультимедийном пособии «Измерение площадей по топографическим картам и планам» [12] и в лекции №5 [9], с которыми можно ознакомиться
вэлектронной библиотеке университета и на кафедре «Землеустройство и геодезия».
1.7.4 Задание 6 Измерение площадей аналитическим, графо-аналитическим
и механическим способами
Студенты измеряют площадь заданного им полигона (четырехугольника) как сумму двух треугольников, а также рассчитывают ее по прямоугольным координатам вершин четырехугольника и определяют с помо-
31
щью планиметра PLANIX 7. Данные измерений вносятся в табл. 8. В табл. 8 приведены площади четырехугольника 1–2–3–4, вычисленные тремя разными способами.
|
|
|
Таблица 8 |
|
Аналитический способ |
|
|
|
|
|
|
Наименование |
Вычисление площади |
Вычисление площади по- |
Механический |
как суммы площадей |
лигона по прямоуголь- |
способ |
|
|
простых геометриче- |
ным координатам его |
|
|
ских фигур |
вершин |
|
Площадь, м² |
519984 |
519785 |
520500 |
|
|
|
|
Площадь, га |
51,998 |
51,98 |
52,05 |
|
|
|
|
Полученныерасхожденияменее0,1 гаможносчитатьнесущественными.
1.8. Рельеф местности и его изображение. Определение абсолютных отметок точек по топографическим картам
Под рельефом местности подразумевается совокупность неровностей земной поверхности. Рельеф местности – важнейший элемент содержания топографических карт. Учету рельефа при всех видах строительства придается первостепенное значение. На современных картах рельеф изображается горизонталями.
Горизонталь – это замкнутая кривая, соединяющая точки с одинаковыми высотными отметками и имеющая следующие свойства:
а) горизонтали – замкнутые кривые, б) горизонтали не пересекаются,
в) чем меньше расстояние между горизонталями на карте, тем круче скат на местности и наоборот.
Расстояние между горизонталями по отвесной линии называется высотой сечения рельефа, она подписывается на картах под линейным масштабом. Расстояние между горизонталями в плане называется заложением. В зависимости от масштаба карты и характера рельефа высота сечения может быть равна 1; 2; 5, 10 метров и т.д. При слабовыраженном рельефе или более точном его изображении горизонтали могут проводиться через 0,25 и 0,5 м. Горизонталь представляет собой линию, полученную при пересечении поверхности земли плоскостью, параллельной ее уровенной поверхности (рис.20).
Для выделения различных форм рельефа, изображенного горизонталями, направления скатов обозначают черточками (бергштрихами), а также надписями ( численные значения), где основание цифр направлено в сторону понижения местности. Мерой крутизны ската линии служит ее уклон
32
i, который определяется тангенсом угла наклона: i = tg γ = h/d, где h – превышение между двумя точками; d – горизонтальное проложение (расстояние между этими точками на плане, рис.21). Горизонтальное проложение является проекцией измеряемой линии на местности на плоскость, d = D · cosγ.
 Высота сечения рельефа
Высота сечения рельефа
Горизонтали
План
Заложение
Рис.20. Схема построения горизонталей
D
h
γ
d
Рис. 21. Соотношение горизонтальных проложений (d) и длин сторон (D)
Из многочисленных форм рельефа можно выделить:
1.Основание горы – подошва, наивысшая точка – вершина, вершина в виде площадки – плато.
2.Котловина, впадина – чашеобразные замкнутые со всех сторон углубления, нижняя часть – дно, верхний край – бровка.
3.Хребет – вытянутая возвышенность, понижающаяся в одном направлении, имеющая два крутых склона, пересечение которых образует ось, называемую водораздельной линией.
4.Лощина – вытянутое углубление местности, понижающееся в одном направлении. Нижняя часть лощины образует водослив или тальвег.
5.Седловина – пониженная часть местности между двумя соседними возвышенностями.
33

1.8.1. Определение отметок точек по топографической карте
Для определения отметок точек по топографической карте необходимо знать высоту сечения рельефа (на карте рис.1. горизонтали проведены через 2,5 метра), направление ската и отметки горизонталей.
Например: на рис.22 показан фрагмент топографической карты. Требуется определить абсолютные отметки точек 1, 2 и построить продольный профиль по линии 1–2. Точка 2 лежит на горизонтали, следовательно, ее отметка равна отметке горизонтали Н2 = 155,00 м. Проводим через точку 1 прямую, кратчайшее расстояние между горизонталями.
Измеряем расстояние d от младшей горизонтали до точки 1 и замеряем расстояние D между горизонталями (см. рис. 22). Отметка точки 1 равна:
Н1 = Н0 + [(d /D) · (145 – 142,5)] = 142,5 +[(1,4 / 1,7) · 2,5] = 144,56 м,
где Н0 – отметка младшей горизонтали, между которыми расположена точка 1; d – расстояние в сантиметрах от младшей горизонтали до точки 1; D – расстояние между горизонталями; 2,5 – высота сечения рельефа.
2
· 155.6
· 145.7
45
d
1
D
· 156.6
150 |
155 |
Рис. 22. Определение отметок точек по горизонталям
Определяем превышение между точками 1 и 2:
h1-2 = H2 – H1 = 155 – 144,56 = 10,44 м.
Расстояние между точками 1и 2 равно d1-2 = 910 м. Тогда уклон по линии 1–2 будет равен:
ί1-2 = h1-2 / d1-2 = 10,44 / 910 = 0,0115. 34
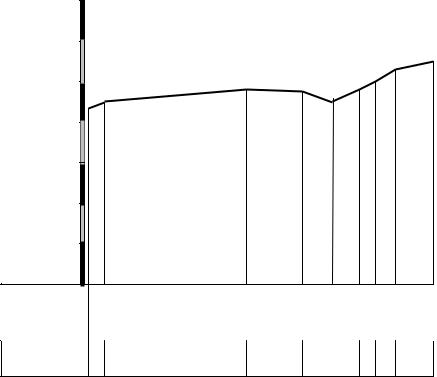
1.8.2. Построения продольного профиля по заданному направлению
Построение профиля по линии 1–2 начинаем с определения на ней положения горизонталей, т.е. горизонтали переносятся на линию 1–2. Затем линия 1–2 разворачивается в горизонтальное положение и определяются абсолютные отметки крайних точек 1; 2 (см. рис. 22). Профиль строится в 1:10000 в горизонтальном масштабе и для выразительности – в 1:1000 в вертикальном масштабе. Все необходимые для построения профиля данные заносятся в графы (сетки профиля), расположенные в нижней части профиля. На листе миллиметровой бумаги строим графы расстояний и отметок (рис. 23). Сетка профиля строится таким образом, чтобы верхняя граница верхней графы совпала с утолщенной линией миллиметровки. Начало профиля также выбирается на утолщенной линии, в 5–7 сантиметрах от края листа. Верхняя граница сетки профиля совпадает с линией условного горизонта, которая выбирается таким образом, чтобы наименьшая отметка горизонтали была на 4 сантиметра выше линии условного горизонта. Определяем отметку условного горизонта.
170 |
|
|
|
|
|
|
|
|
|
160 |
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
|
|
140 |
|
|
|
|
|
|
|
|
|
130 |
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|
110 |
|
|
|
|
|
|
|
|
|
УГ=100 м |
|
|
|
|
|
|
|
|
|
Отметки |
144.56 |
145.00 |
147.50 |
147.50 |
145.70 |
147.50 |
150.00 |
152.50 |
155.00 |
|
|||||||||
Расстояния |
40 |
350 |
14 0 |
|
14 0 |
40 50 |
90 |
||
|
|
Масштабы: горизонтальный |
1:10000 |
|
|
|
|
||
|
|
вертикальный |
1:1000 |
|
|
|
|
||
Рис.23. Профиль по линии 1–2 |
|
|
|
|
|
||||
Например: наименьшей горизонталью, пересекающей линию 1–2, является горизонталь, имеющая отметку 145 метров выше уровня моря. Линия условного горизонта на 4 см ниже отметки 145 метров. В 1:1000 масштабе это соответствует 40 метрам. Следовательно, линия условного горизонта равна: 145 – 40 = 105 метров. Для удобства отсчетов принимаем ли-
35
нию условного горизонта, равную 100 метрам. Из точек пересечения линии профиля и горизонталей восстанавливаем перпендикуляры, на которых откладываем в масштабе 1:1000 разницу между отметкой горизонтали и отметкой условного горизонта. Полученные точки соединяем между собой. В результате получается рельеф местности по линии 1–2.
1.8.3. Задание 7
Определение отметок точек по топографической карте. Построение продольного профиля по заданному направлению
В задании 7 студенты определяют отметки крайних точек по одному из направлений четырехугольного полигона. Причем направление выбирается таким образом, чтобы оно пересекалось с максимальным количеством горизонталей. Например: в четырехугольном полигоне 1–2–3–4 (см. рис. 1) таким направлением является линия 2–3. После определения абсолютных отметок крайних точек по линии 2–3 строится продольный профиль в масштабах: горизонтальный 1:10000, вертикальный 1:1000.
1.9. Искажение длин и площадей в проекции Гаусса – Крюгера
Проекция Гаусса – Крюгера является конформной, т.е. при переходе с эллипсоида на плоскость в ней сохраняется подобие бесконечно малых фигур. По мере удаления от осевого меридиана происходит искажение длин линий и площадей. Максимальные искажения характерны для краев зон.
1.9.1. Искажение длин линий в проекции Гаусса — Крюгера
Из подобия бесконечно малых фигур следует, что их стороны будут пропорциональны. Пусть расстояние между точками 1 и 2 равно S, тогда в проекции Гаусса – Крюгера расстояние между ними будет равно:
Sr = S [1 + (Y2m / 2R2)],
где Ym – ордината средней точки линии 1–2; R = 6371 км (радиус Земли). Разность ∆S = Sr – S – это поправка в длину линий при переходе с эл-
липсоида на плоскость в проекции Гаусса – Крюгера.
∆S = S · (Y2m / 2R2).
Расстояние в проекции будет всегда больше расстояния на эллипсоиде. Для расстояний, расположенных на осевом меридиане, ∆S = 0. По мере удаления от осевого меридиана эта поправка возрастает и достигает максимальных значений на краю зоны.
Например: определяем искажение длины линии 1–2. Координата точ-
ки 1 – Y1= 6420222, координата точки 2 – Y2 = 6420830,75 (см. табл. 6), тогдаYm = (420222 + 420830,75) / 2 = 420526 – 500000 = – 79473,63 м= –79,47 км.
36
Длина линии на карте равна Sr = 614,04 м (см. табл. 7). Требуется определить длину линии на местности и величину искажения при переносе ее с карты на местность.
S = Sr / [1 + (Y 2m / 2R2 )] = 614,04 / [1+ (–79,472 / 2· 63712)] = 613,99 м.
Так как мы переносим линию с карты на местность, то:
∆S = S – Sr = 613,99 – 614,04 = – 0,05 м.
Относительное искажение длины линии равно:
1/ N = ( S : S) / (S : S) = 1/12280.
1.9.2.Искажение площадей в проекции Гаусса — Крюгера
Впроекции Гаусса – Крюгера помимо искажения длин линий получается искажение площадей участков земной поверхности. Если площадь участка на эллипсоиде равна Р, то соответствующая ему площадь на плоскости в проекции Г–К равна:
Pr = P · [1+ (Y 2m / R2)].
Разность ∆Р = Рr – P – это поправка за искажение площади при переходе от с поверхности эллипсоида на плоскость в проекции Гаусса – Крюгера.
∆P = P · (Y 2m / R2),
где Ym – ордината средней точки участка. Для земельного участка, расположенного вблизи осевого меридиана, поправка ∆Р = 0. По мере удаления от осевого меридиана поправка за искажение площади будет заметно возрастать.
Например: по топографической карте (см. рис.1) измерена площадь четырехугольного участка 1–2–3–4, которая равна 51,98 га (см. табл. 8). Требуется определить площадь участка при переносе его с топографической карты на местность. Определяем ординату средней точки участка:
Ym = (Y1+Y2+Y3+Y4) / 4 = (420222 + 420830,75 +421021,18 + 420257,16) / 4 = =420582,77 – 500000 = – 79417,23 м = – 79,42 км.
Определяем площадь участка на местности.
P = Pr / [1 + (Y 2m / R2)] = 51,98 / [1+ (–79,472 / 63712)]= 51,97 га.
Так как мы переносим площадь участка с карты на местность, то:
P =P – Pr = 51,97 – 51,98 = – 0,01 га.
Относительное искажение площади равно: 1 / N = 1 / 5197 1/5000.
37
1.9.3. Задание 8
Определение искажений в проекции Гаусса — Крюгера при переносе длин линий и площадей участков с карты на местность
В данном задании студенты определяют поправки за искажение длин линий и площадей при переносе их с карты на местность, т.е. с плоскости в проекции Гаусса – Крюгера на земной эллипсоид. Исходными данными являются длины сторон и площадь четырехугольного полигона 1–2–3–4, а также координаты вершин полигона, полученные аналитическим способом (см. табл. 5). Определяются относительные искажения длины одной из сторон и площади полигона.
|
|
|
|
Таблица 9 |
Наименование |
Величина |
Величина |
Искажение |
Относительное |
|
на карте |
на местности |
величин |
искажение 1/N |
Длина линии 1–2 |
614,040 м |
613,99 м |
– 0,05 м |
1/12280 |
Площадь полигона |
51,98 га |
51,97 га |
– 0,01 га |
1/ 5197 |
1–2–3–4 |
|
|
|
|
Полученные результаты вносятся в табл. 9.
1.10. Разграфка и номенклатура карт и планов
Разграфка, или нарезка карты – это система деления многолистной карты на листы. Чаще всего применяют два вида разгафки: трапецивидная, при которой границами листов служат параллели и меридианы, и прямоугольная, когда карта делится на прямоугольные или квадратные листы одинакового размера (рис. 24). Серии государственных топографических и тематических карт, включающие тысячи листов, имеют в каждой стране стандартную разграфку. Например, в России в основу разграфки топографических карт положена карта 1:1000000 масштаба.
Любой ее лист представляет трапецию, которая ограничена параллелями и меридианами, проведенными через 4° по широте и 6°по долготе. Деление на градусы осуществляется от Гринвичского меридиана и от экватора. Разграфку карт более крупных масштабов получают, деля лист миллионной карты на части. Каждая ячейка разграфки имеет свою номенклатуру – систему обозначения отдельных листов. Листы карты 1:1000000, заключенные между смежными параллелями, образуют пояса, которые обозначаются заглавными буквами латинского алфавита A, B, …., V, Z. В северном полушарии имеется 22 полных пояса и один неполный. Листы масштаба 1:1000000, заключенные между смежными меридианами, составляют колонны, которые нумеруют арабскими цифрами 1, 2, …, 60, начиная с меридиана с долготой 180°, в направлении с запада на восток.
38
30°00’ |
|
N – 36 |
36°00’ |
30°00’ |
|
|
|
|
|
N – 36 |
|
|
|
36°00’ |
|||||||||||||||
56° |
|
|
|
|
|
|
|
56° |
56° |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
56° |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
00’ |
|
|
|
|
|
|
|
00’ |
00’ |
|
Ι |
|
|
ΙΙ |
|
|
ΙΙΙ |
|
ΙV |
|
V |
|
VΙ |
|
|
00’ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55°20’ |
|
|
|
|
А |
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
54°40’ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
54°00’ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
53°20’ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52°40’ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52° |
|
|
|
|
|
|
|
52° |
52° |
|
|
|
|
|
|
|
|
|
|
|
|
|
XXXV |
|
Ι52° |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
00’ |
|
|
|
33°00’ |
|
|
|
00’ |
00’ |
|
|
31° |
32° |
33° |
34° |
35° |
|
00’ |
|||||||||||
|
|
|
|
||||||||||||||||||||||||||
30°00’ |
1: 500000 |
36°00’ |
30°00’ |
|
|
|
1: 200000 |
|
|
|
36°00’ |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
N – 36 – A |
|
|
|
|
|
|
|
|
|
|
|
|
|
N – 36 – XX |
|
|
|
|
|
|||||
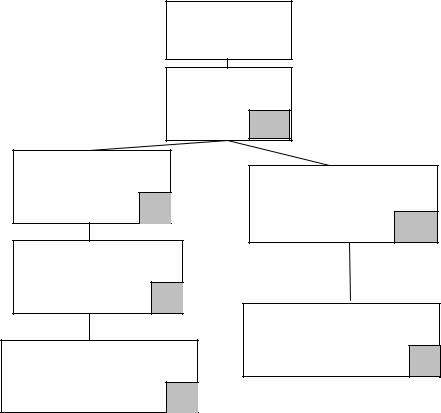
Рис. 24. Схема разграфки листа карты 1:1000000 масштаба N – 36 на листы карт масштабов 1:500000 и 1:200000. Заштрихованы листы N – 36 – A и N – 36 – XX
Номенклатура листа карты 1:1000000 масштаба состоит из буквы, обозначающей пояс, и числа – номера колонны, например N – 36 (рис. 25).
1:1000000 N – 36
1:100000 N – 36 – 144
144
1:50000
N – 36 -144 – Г
4
1:25000
N – 36 – 144 – Г – г
4
1:10000
N – 36 – 144 – Г – г – 4
4
1:5000
N – 36 – 144 – Г – (256)
256
1:2000
N – 36 – 144 – Г – (256 – N)
9
Рис.25. Схема образования листов топографических карт
39
При переходе к листам более крупных масштабов делят лист карты 1:1000000 масштаба меридианами и параллелями таким образом, чтобы листы карт более крупных масштабов были примерно одинаковых размеров.
Разделив каждую сторону рамки карты масштаба 1:1000000 на 12 частей, получают 144 листа карты 1:100000 масштаба. Каждый лист карты 1:100000 масштаба имеет размеры: 30' по долготе и 20' по широте. Их последовательно нумеруют цифрами от 1 до 144. Таким образом, лист карты с номером 144 имеет номенклатуру N – 36 – 144. В основу номенклатуры листов топографических карт более крупных масштабов положена номенклатура листов 1:100000 масштаба (см. рис. 25).
В нижнем правом углу каждого прямоугольника показано число листов топографических карт, соответствующее листу карты более мелкого масштаба, а внутри него приведены номенклатура последнего листа карты и ее масштаб. Размеры листов топографических карт, показанные на рис.25, приведены в табл. 10.
|
|
|
Таблица 1 0 |
Масштаб карты |
|
Размер листа по: |
|
|
Широте |
|
Долготе |
1:1000000 |
4° |
|
6° |
1:100000 |
20' |
|
30' |
1:50000 |
10' |
|
15' |
1:25000 |
5' |
|
7'30" |
1:10000 |
2'30" |
|
3'45" |
1:5000 |
1'15" |
|
1'52,5" |
1:2000 |
25' |
|
37,5" |
Разгафка и номенклатура топографических планов масштабов 1:5000, 1:2000, 1:1000, 1:500, составленных в местных системах координат, отличаются от изложенных ранее. Для планов таких масштабов принимают прямоугольную разграфку, которую получают следующим образом. Сетку прямоугольных координат проводят на планах всех масштабов через 10 сантиметров.
В основу разграфки для образования номенклатуры планов принимают
лист 1:5000 масштаба, с размерами рамки 40 40 см (2 2 км на местности). Номенклатурой плана 1:5000 масштаба является ее номер, обозначенный арабской цифрой. Размеры рамок планов более крупных масштабов составляют 50 50 см (рис.26).
В нижнем правом углу каждого прямоугольника показано число листов топографических планов, соответствующее листу плана более мелкого масштаба, а внутри него приведена номенклатура последнего листа плана и его масштаб.
40
