1459

2. Произведение (пересечение) множеств А и В есть множество С=А В (или С=АВ), состоящее из элементов, одновременно при9 надлежащих множеству А и множеству В (А А=А).

АВ

À Â

Если АВ , то А и В не пересекаются.

3. Разность множеств А и В есть множество С=А\В, состоящее из элементов А, не содержащихся в В.

В общем случае (А\В)+В А.

А\В

À Â

1.А+В=В+А.

2.(А+В)С=АС+ВС.

3.(АВ)С=А(ВС).

4.(А+В)+С=А+(В+С).

Логические символы:

1.– из предложения следует предложение .

2.– предложения и эквивалентны: из следует , из следует .

3.х А: – для всякого элемента х А имеет место предложение ( – квантор всеобщности).

Кванторы (от лат. quantum – сколько) – логические эквиваленты слов «все», каждый и т.п.

4.y B: – существует элемент y B, для которого имеет место предложение ( – квантор существования).

5.– не ; отрицание предложения .

Отрезок, интервал, ограниченное множество

1.Отрезок, сегмент [a,b] – множеcтво чисел х, удовлетворяющих неравенствам: a x b.

2.Интервал, открытый отрезок (a,b): a x b.

3.Полуоткрытые отрезки, полуинтервалы [a,b), (a,b]: a x b;.

x b.

4. Окрестность точки с – интервал (a,b): a c b.

61

5. – окрестность точки с: (с– , с+ ). Неравенства для абсолютных величин:

1.a a ;

2.a b b a b ;

3.a b a b.

a b a b .

Предел последовательности. Сравнение величин

Пусть каждому n=1,2,3,… поставлено в соответствие число хn. Этим

определена последовательность чисел

xn x1, x2, x3, .

Говорят, что переменная xn пробегает значения последовательностиxn , хn – элементы xn .

Примеры

Впримерах 1, 2, 3 последовательности ограничены.

Впримере 4 последовательность ограничена снизу, но не огра9 ничена сверху.

Определение. Число а называется пределом последовательности

62

Теорема 1. Если переменная хn имеет предел, то он единственный. Теорема 2. Если {xn} сходится, то она ограничена.

Теорема 3. Если последовательность действительных чисел не убывает (не возрастает) и ограничена сверху (снизу) числом М (соответственно m), то существует действительное число а, не превышающее М (не меньшее m), к которому эта последовательность стремится как к своему пределу:

lim xn a M

n

(соответственно lim xn a m ).

n

0 lim xn 1.

n

Арифметические действия с переменными, имеющими предел

Если существуют конечные пределы {xn}, {yn}, то существуют и пределы последовательностей:

{xn + yn}, {xn – yn}, {xn yn}, xn .

yn

При этом

lim(x n y n )=limx n limy n ;

lim(x n y n )=limx n limy n ;

В последнем случае предполагается, что limyn 0.

Число e определяется как предел ограниченной и возрастающей последовательности

63

Функция

Пусть Е – множество чисел. И пусть каждому х Е поставлено в соответствие одно число y Е1. Тогда говорят, что на Е задана однозначная функция y=f(x).

Е – область задания f(x);

Е1 – область значений f(x) (образ множества Е). Пусть

Е1 = f ( Е ) ;

Е2 = F ( Е 1 ) .

Имеем

Е 2 = F ( f ( Е ) ) .

Функция z=F(f(x)), z Е2, y Е1, x Е называется сложной функцией

или суперпозицией f и F.

Если в образовании сложной функции участвует n функций, то

z = F 1 ( F 2 ( F 3 ( … ( F n ( x ) … ) ) ) ) .

Пример.

z atg x2 1. Здесь z au 1, w au, u tg v, v x2;

z=F1(F2(F3 ((F4(x))))); v F4 x x2; u F3 x tg v; w F2 u au; z F1 w w 1.

Способы задания функций

1.Аналитически (формулой)

2.Графически

3.Таблично

4.Программой для ЭВМ.

Функция называется четной, если f(–x)= f(x) и нечетной, если f(–x)= –f(x).

Произведение четной функции на нечетную есть нечетная функция. Произведение двух четных или нечетных функций есть четная

функция.

Если f(x+T)=f(x) (T 0 ) x из ОДЗ, то функция называется перио дической.

Если каждому x E поставлено в соответствие множество несколь9 ких чисел y, то говорят, что определена многозначная функция у= f(x).

64

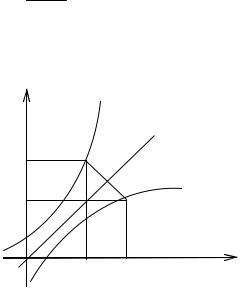
Функция одной переменной может быть задана неявно уравнением F(x,y)=0.Переход к явному заданию функции от неявного не всегда возможен.

Если y= f(x) осуществляет взаимно однозначное отображение Е в E1, то и каждому у Е1 ставится в соответствие единственное x Е (определяется функция y= (x)). Функции y= f(x) и y= (x) назы9 ваются взаимно обратными.

Способы определения взаимно обратных функций.

1. Если y= f(x), то уравнение y– f(x)= 0 определяет х как неявную функцию от у. Чтобы получить ее явное выражение, надо (если возможно) разрешить это уравнение относительно х, то есть представить в виде y= (x). Функции y= f(x), y= (x) будут взаимно обратными. Например:

y10x; y 10x 0 10x y; x lg y.

2.Если функция сразу задана в неявном виде, то, разрешая это

уравнение сначала относительно y, затем – x, найдем взаимно обратные функции y= f(x), y= (x). Например:

x 2y 1 0.

y 1 x ; x 2y 1 . 2

Графики функций y= f(x), y= (x) расположены симметрично относительно прямой y= x.

y= x

M (b,a)

(b)=a

y= f(x)

Функция y= f(x) называется возрастающей в интервале, если большим значениям x соответствуют бульшие значения y. Аналогично определяется убывающая функция.

Интервалы возрастания и убывания функции называются интер9 валами монотонности функции.

65

Для всех точек, лежащих в 9интервале, график y = f(x) лежит внутри полосы шириной 2 .

Заметим, что для существования lim f x не требуется, чтобы

x x0

функция была определена в самой точке х0.

Число A1 (A2) называется пределом функции f(x) в точке х0 слева (справа), если f(x) A1(A2) при х х0, и при этом х принимает лишь значения, меньшие (большие) х0.

Можно доказать, что если существуют А1 и А2, где А1 = А2=А, то

lim f x A.

x x0

И обратно: если существует

lim f x A ,

x x0

66

то существуют пределы слева и справа, при этом

lim f x A,

x x0 0

lim f x A.

x x0 0

Предел функции в бесконечности

Число А называется пределом y= f(x) при x , если для всех достаточно больших значений х соответствующие значения f(x) как угодно мало отличаются от А ( 0, x0 0 : x x0 f x A ).

Пишут

lim f x A

x

или

f ( x ) А ( x ) .

Аналогично определяется lim f x .

x

f(x)

A+

А

A–

При x (х х0) график y= f(x) будет находиться в полосе, огра9 ниченной прямыми y=A – ; y=A + .

Ограниченность функции, имеющей предел

67

и на некоторой окрестности u(x0), x x0 имеет место

и на некоторой окрестности u(x0), x x0

f1 x x f2 x ,

то

lim x A.

x x0

Бесконечно большие величины

Определение. Функция y=f(x) называется бесконечно большой величиной при x x0, если для всех значений x, достаточно мало отличающихся от x0, соответствующие значения f(x) по абсолютной величине превосходят любое наперед заданное сколь угодно большое

Иначе говоря, какое бы большое число М не взяли, найдется такое>0, что при x x0 будем иметь f x M .

Не смешивать бесконечно большое число с большим постоянным числом!

Бесконечно малые величины

Определение. Функция у = f(x), стремящаяся к нулю при x x0, называется бесконечно малой величиной при x x0. Например:

y=x2 при x 0, y 0; y=x–1 при x 1, y 0.

Не смешивать постоянное очень малое число с бесконечно малой величиной! Единственным числом, которое рассматривается в качестве бесконечно малой величины, служит нуль (и то лишь потому, что предел постоянной величины равен ей самой).

Теорема. Если функция f(x) – бесконечно большая величина, то

1

f x – бесконечно малая величина.

68

Теорема (прямая). Если функция имеет предел, то ее можно представить как сумму постоянной, равной ее пределу, и бесконечно малой величины, то есть

f(x) = А+ (х).

Теорема (обратная). Если функцию можно представить как сумму постоянной и бесконечно малой величины, то постоянное слагаемое

есть предел функции, то есть из f(x) = А+ (х), следует lim x 0.

x x0

Правила предельного перехода

Теорема. Сумма конечного числа бесконечно малых величин есть бесконечно малая величина.

Следствия:

1. Предел суммы конечного числа слагаемых равен сумме пределов этих слагаемых, если существуют пределы слагаемых.

2. Произведение ограниченной функции на бесконечно малую величину есть бесконечно малая величина.

3. Предел произведения конечного числа множителей равен произведению пределов этих множителей, если существуют пределы сомножителей.

4. Частное от деления бесконечно малой величины на функцию u, предел которой отличен от нуля, есть бесконечно малая величина.

4 . Предел частного равен частному от деления пределов, если существуют пределы числителя и знаменателя, и предел знаменателя не равен нулю.

Пример 2. Найти

lim x2 4 .

x 2 x 2

0 Имеем неопределенность вида 0 :

69

Указанное преобразование справедливо при всех х 2. Поэтому, по определению предела, где в самой точке х0 функция может быть и не определена, будем иметь:

бесконечно большая величина.

Пример 3.

1

Найти lim .

x 1 x 1

При х 1

70