
1459
.pdf
Координаты точки C x, y , делящей отрезок M1M2 в отношении :
x |
x1 x2 |
, |
y |
y1 y2 |
. |
1 |
|
||||
|
|
|
1 |
||
В полярной системе координат точка М плоскости определяется полярным радиусом9вектором точки r OM и полярным углом , обра9
зованным отрезком OM с полярной осью Ox ( положителен при отсчете от полярной оси против часовой стрелки). Если точка M имеет полярные координаты r 0 и 0 2 , то ей же отвечает и бесчисленное мно9
жество пар полярных координат r, 2k , где k Z.
Если начало О декартовой прямоугольной системы координат совместить с полюсом, а ось Ox направить по полярной оси, то имеет
место: |
|
|
|
x r cos , |
y r sin ; |
||
r x2 y2 , |
tg |
y |
. |
|
|||
|
|
x |
|
Уравнение линии
Линии (множеству точек M(x,y)) на плоскости xOy соответствует уравнение, связывающее x и y. Координаты точки М линии удовлетворяют этому уравнению. Координаты любой другой точки не удовлетворяют уравнению линии. Например, точка A 2,4 лежит, а
B 1,3 не лежит на параболе y x2 .
Аналогично определяется уравнение линии в полярных координатах.
Часто линия определяется параметрическими уравнениями x x t , y y t . Исключение (если оно возможно) параметра t из этой
системы приведет к обычному уравнению линии вида f x, y 0 .
Общее уравнение прямой на плоскости имеет вид:
Ax By D 0 ,
где A,B,D – постоянные коэффициенты, A2 B2 0 . В частном случае при:
D 0 и A, B 0 прямая проходит через начало координат; A 0, B, D 0 – параллельна оси Оx,
B 0, A, D 0 – параллельна Оy,
B, D 0, A 0 – совпадает с осью Оy,
21

A, D 0, B 0 – совпадает с осью Оx.
При B 0 , разрешив общее уравнение прямой относительно y, получим уравнение прямой с угловым коэффициентом
y kx b , где k BA tg – угловой коэффициент;
– угол между прямой и положительным на9 правлением Оx;
b DB – ордината точки пересечения прямой с осью Оy.
При D 0 уравнение прямой можно представить в виде уравнения в отрезках
|
|
|
|
|
|
x |
|
y |
|
1. |
|
|||
|
|
|
|
|
|
a |
b |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Здесь a |
D |
, b |
D |
есть |
соответственно абсцисса |
и ордината |
||||||||
A |
B |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
точек пересечения прямой с осями Оx и Оy. |
|
|||||||||||||
Уравнение прямой, проходящей через M1 x1, y1 и |
M2 x2, y2 , |
|||||||||||||
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
y y1 |
|
|
x x1 |
|
|
||||
|
|
|
|
|
|
x2 x1 |
|
|||||||
|
|
|
|
|
y2 y1 |
|
|
|||||||
и угловой коэффициент этой прямой находится по формуле
k y2 y1 . x2 x1
Если x1 x2 , то уравнение прямой, проходящей через точки M1 и M2, имеет вид x x1 ; при y1 y2 соответствующее уравнение прямой: y y1 .
Угол между прямыми. Пересечение прямых. Расстояние от точки до прямой
Углом между прямыми называется наименьший из двух смежных углов, образованных этими прямыми. Так что угол между прямыми y k1x b1 и y k 2 x b2 определяется из
tg |
|
k2 k1 |
|
. |
||
1 k k |
||||||
|
|
|||||
|
1 |
2 |
|
|
||
22

Условие параллельности прямых: |
|
|
|
|
|
|||||||
|
|
|
|
|
|
k1 k2 |
; |
|
|
|
|
|
условие перпендикулярности: |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
k |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
k2 |
|
||||
|
|
|
|
|
|
|
|
|||||
Если |
A1 |
|
B1 |
(при их равенстве прямые параллельны), координаты |
||||||||
A |
|
|||||||||||
|
|
B |
|
|
|
|
|
|
|
|||
2 |
2 |
|
|
|
|
|
|
|
|
|
||
точки пересечения прямых A1x B1y D1 0 |
и A2 x B2 y D2 0 |
|||||||||||
находятся путем совместного решения уравнений этих прямых. |
||||||||||||
Расстояние d от точки M x0 , y0 |
до прямой |
Ax By D 0 опре9 |
||||||||||
деляется по формуле |
|
|
|
|
|
|
|
|||||
|
|
|
|
d |
|
Ax0 By0 D |
|
. |
|
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
A2 B2
Кривые второго порядка
Кривая второго порядка задается уравнением
Ax2 2Bxy Cy2 2Dx 2Ey F 0 .
Перечислим основные их виды.
Окружность как множество точек, равноудаленных от центра C a,b , описывается уравнением
x x0 2 y y0 2 R2 ,
где r – радиус окружности.
Эллипс определяется как множество всех точек плоскости, сумма расстояний которых до двух заданных точек (фокусов) есть величина постоянная, равная 2a и превышающая расстояния между фокусами. Если в прямоугольной системе координат в качестве фокусов выбраны точки F1 c,0 и F2 c,0 , то получится каноническое (простейшее)
уравнение эллипса:
x2 y2 1, a2 b2
где a и b – полуоси эллипса. Справедливо соотношение:
a2 b2 c2 .
23

Вид эллипса приводится на рис. 1. |
|
|
|
y |
|
|
|
M |
r2 |
|
r1 |
|
|
x |
F2(–c,0) |
0 |
F1(c,0) |
Рис. 1
Мера сжатия эллипса определяется его эксцентриситетом ac 1.
Расстояния r1 и r2 точки М эллипса от его фокусов F1 и F2 называются фокальными радиусами9векторами этой точки, r1 r2 2a .
При a b r ( c 0 , 0 ) эллипс превращается в окружность x2 y2 r 2 .
Справедливо:
r1 a x , r2 a x .
Гипербола определяется как множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек (фокусов) F1 и F2 есть величина постоянная, равная 2a и меньшая расстояния между фокусами. Если фокусы гиперболы есть точки F1 c,0 и F2 c,0 , то каноническое уравнение гиперболы имеет
вид:
x2 y2 1, a2 b2
где a и b – полуоси гиперболы.
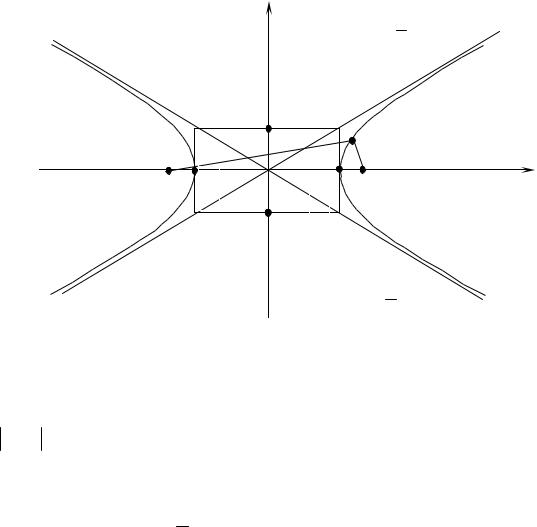
Вид гиперболы приводится на рис. 2.
24
|
|
y |
y |
b x |
|
|
|
||
|
|
|
|
a |
|
|
B1(0;b) |
|
|
|
|
|
M |
x |
|
|
|
|
|
F1(–c,0) |
A2 |
A1 |
F1(c,0) |
|
|
||||
|
|
|||
B2(0;–b)
y ab x
Рис. 2
На рисунке A1 a,0 , A2 a,0 – вершины гиперболы. Отрезок A1A2
( A1A2 2a ) называется действительной осью гиперболы, а отрезок
B B |
( |
|
B B |
|
2b ) – ее мнимой осью. Прямые y |
b |
x, y |
b |
x – асим9 |
||
|
|
||||||||||
|
|
|
|
||||||||
1 |
2 |
|
|
1 |
2 |
|
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|||
птоты гиперболы; ac 1 – эксцентриситет гиперболы. Справедливо:
b2 c2 a2 .
Гипербола симметрична относительно Ox и Oy.
Для правой ветви гиперболы фокальные радиусы9векторы равны: r1 x a, r2 x a .
Для левой ветви:
r1 x a, r2 x a .
При a b получится равнобочная гипербола: x2 y2 a2 .
Две гиперболы называются сопряженными, если они имеют одни и те же полуоси и асимптоты, но действительная ось одной служит мнимой осью другой, и наоборот.
Парабола определяется как множество всех точек плоскости, равноудаленных от данной точки (фокуса) F и данной прямой (дирек9 трисы). Каноническое уравнение параболы получится, если директрисой
25
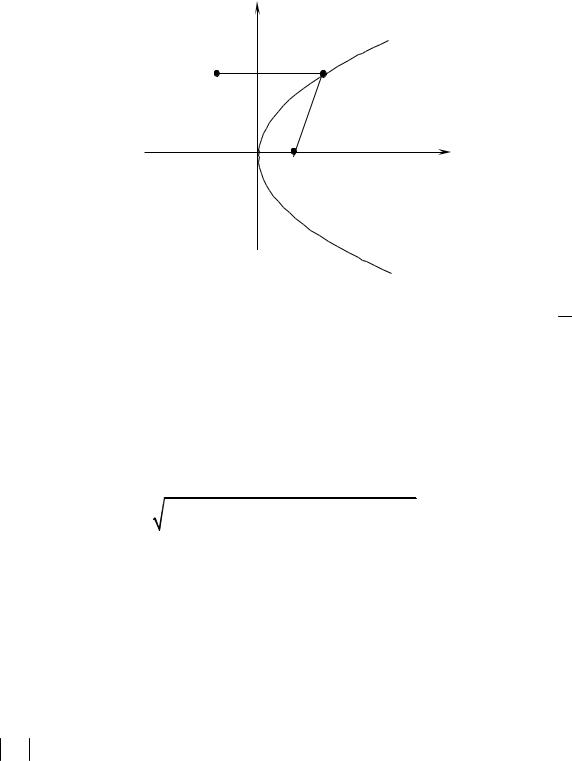
является прямая x |
p |
, а |
фокусом – |
точка |
p |
,0 |
|
, и будет иметь |
||||||
|
|
F |
|
|
||||||||||
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 2 px . |
|
|
|
|
|
|
|
|
Вид этой параболы приводится на рис. 3. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
p |
|
0 |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
;0 |
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3
Длина фокального радиуса9вектора определится в виде r x 2p
( p 0 ).
1.4. Аналитическая геометрия в пространстве
Расстояние между точками A x1, y1, z1 |
и B x2, y2, z2 вычисляется |
||||||||||||||
по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
x |
2 |
x |
2 y y 2 z |
2 |
z 2 . |
||||||||
|
|
|
|
|
1 |
2 |
1 |
|
|
1 |
|
||||
Если отрезок с концами в точках A x1, y1, z1 и B x2, y2, z2 делится |
|||||||||||||||
точкой C x, y, z |
в отношении , |
то координаты точки С опреде9 |
|||||||||||||
ляются по формулам |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
x1 x2 |
, |
y |
y1 y2 |
, |
z |
z1 z2 |
. |
||||||
|
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
||||
Цилиндрические координаты. Положение точки M(x,y,z) в про9 странстве можно определить ее аппликатой z и полярными координатами r OP и xOP проекции P этой точки на координатную плоскость
26

xOy. Величины r, , z называются цилиндрическими координатами точки М. Декартовы прямоугольные и цилиндрические координаты точки связаны соотношениями x r cos , y r sin (аппликаты в обеих системах одинаковы).
Сферическая система координат задает положение точки M(x,y,z) следующими тремя величинами: расстоянием r OM , угломzOM и углом между плоскостями zOx и zOM. Величины r, , называются сферическими координатами точки М. Прямоугольные и сферические координаты связаны соотношениями:
x r sin cos , y r sin sin , z r cos .
Векторы
Вектором называется направленный отрезок AB, у которого точка A рассматривается как начало, а точка В — как конец.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.
Вектор a может быть единственным образом представлен в виде a xi yj zk
(разложение вектора a по осям координат или разложение по ортам). Здесь x,y,z – проекции вектора a на соответствующие оси координат
(координаты вектора a ), i , j , k – орты этих осей (единичные векторы, направления которых совпадают с положительными направлениями соответствующих осей).
Векторы xi , yj , zk называются составляющими (компонентами)
вектора |
|
|
|
|
по осям координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Длина (модуль) вектора |
|
|
обозначается |
|
|
|
|
|
|
|
и |
определяется по |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
a |
a |
|||||||||||||||||||||||||||||||||||||||||||
формуле |
|
|
|
|
|
|
|
x2 y2 z2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Направление вектора |
|
определяется по направляющим косинусам |
||||||||||||||||||||||||||||||||||||||||||
a |
||||||||||||||||||||||||||||||||||||||||||||
углов , , , образованных |
|
|
с осями |
координат |
(направляющие |
|||||||||||||||||||||||||||||||||||||||
a |
||||||||||||||||||||||||||||||||||||||||||||
косинусы) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
x |
|
, |
cos |
|
y |
|
, |
cos |
|
|
z |
|
; |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 cos2 cos2 1. |
|
|
|
|
|
|
|||||||||||||||||||||||||
Вектор |
|
= |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
OM |
называется радиусом/вектором точки M. Коорди9 |
|||||||||||||||||||||||||||||||||||||||||
r |
||||||||||||||||||||||||||||||||||||||||||||
наты r совпадают с координатами точки M и разложение вектора r по ортам имеет вид
r xi yj zk .
27

Для точек A x1, y1, z1 и |
B x2, y2, z2 разложение вектора |
|
по |
AB |
|||
ортам имеет вид |
|
|
|
AB x2 x1 i y2 y1 j z2 z1 k .
Его длина совпадает с расстоянием между точками A и B
|
|
|
x |
|
|
2 y y |
2 z |
|
|
2 . |
||
d |
|
|
|
|
x |
|
z |
|||||
AB |
2 |
2 |
||||||||||
|
|
|
|
|
1 |
2 |
1 |
|
1 |
|
||
Направление вектора AB определяется по направляющим коси9 нусам
cos |
x2 x1 |
, |
cos |
y2 y1 |
, |
cos |
z2 z1 |
. |
d |
d |
|
||||||
|
|
|
|
|
d |
|||
Действия над векторами. Скалярное произведение. Произведение вектора на число. Сумма и разность векторов
Произведением вектора |
|
|
на число называется |
вектор |
|
, |
|||||||||||||||||
a |
a |
||||||||||||||||||||||
коллинеарный |
вектору |
|
, |
имеющий модуль |
|
|
|
|
|
|
|
|
|
|
и направленный |
||||||||
|
|
|
|
|
|||||||||||||||||||
a |
|
|
a |
||||||||||||||||||||
одинаково с |
|
, |
если 0 , |
и противоположно |
|
при |
0 . Если |
||||||||||||||||
a |
a |
||||||||||||||||||||||
a x, y, z , то a x, y, z .
Суммой векторов a и b называется вектор a b , который строится следующим образом. Сначала с помощью параллельного
переноса вектора b совмещают его начало с концом вектора a (рис. 4) Сумма векторов a b – «замыкающий» вектор, начало которого со9 впадает с началом вектора a b , а конец — с концом вектора b (правило треугольника).
|
|
|
|
|
|
|
a |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
a |
|
|
|
|
|
|
b |
|
|
||
|
Рис. 4 |
|||||
Разность векторов a b определяется как сумма векторов a и – b (рис. 5). Если a x1, y1, z1 , b x2, y2, z2 , то
a b x1 x2, y1 y2, z1 z2 .
28

b
a b
a
Рис. 5
Вектор, начало которого совпадает с его концом, называется
нулевым и обозначается |
|
. Очевидно, |
|
0,0,0 |
и |
|
|
|
|
|
для |
|||
0 |
||||||||||||||
0 |
0 |
|||||||||||||
a |
a |
|||||||||||||
любого вектора |
|
. |
|
|
|
|
|
|
|
|||||
a |
|
|
|
|
|
|
|
|||||||
Линейные пространства
Множества всех плоских или пространственных векторов, в которых определены операции сложения векторов и умножения вектора на число, являются простейшими примерами векторных пространств.
При этом n9мерным вектором называется упорядоченная совокуп9 ность n действительных чисел, записываемых в виде x x1, x2, , xn , где xi –i9я координата вектора x .
Два n9мерных вектора равны тогда и только тогда, когда равны их соответствующие координаты ( x y , если xi yi , i 1,n ).
Суммой двух векторов одинаковой размерности n называется вектор z x y , координаты которого равны сумме соответствующих
координат слагаемых векторов ( zi xi yi , i 1,n ).
Произведением вектора x на действительное число называется вектор u x , координаты ui которого равны произведению на соответствующие координаты вектора x ( ui xi , i 1,n ).
Линейные операции над любыми векторами удовлетворяют
следующим свойствам: |
|
|
|
||||||||||||||||||||||||||||||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
коммутативное (переместительное) свойство |
||||||||||
x |
y |
y |
x |
||||||||||||||||||||||||||||||
суммы; |
|
|
|
||||||||||||||||||||||||||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– ассоциативное (сочетательное) свойство |
||||||||||||||||
x |
y |
z |
x |
y |
z |
||||||||||||||||||||||||||||
суммы; |
|
|
|
||||||||||||||||||||||||||||||
3) |
|
|
|
|
|
|
– ассоциативное относительно числового множи9 |
||||||||||||||||||||||||||
x |
x |
||||||||||||||||||||||||||||||||
теля свойство; |
|
|
|
||||||||||||||||||||||||||||||
4) |
|
|
|
|
|
|
|
|
– дистрибутивное (распределительное) отно9 |
||||||||||||||||||||||||
x |
y |
x |
y |
||||||||||||||||||||||||||||||
сительно суммы векторов свойство; 29

5) x x x – дистрибутивное свойство относительно сум9 мы числовых множителей;
6) Существует нулевой вектор 0 0,0, ,0 , такой, что x 0 x
для любого вектора x ;
7) Для любого вектора x существует противоположный векторx , такой, что x x 0 ;
8) 1 x x для любого вектора x .
Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше свойствам (рассмат риваемым как аксиомы), называется векторным пространством.
Под x, y, z можно рассматривать не только векторы, но и элементы (объекты) любой природы, удовлетворяющие свойствам 198. В этом случае соответствующее множество R элементов называется линейным
пространством.
Размерность и базис векторного пространства
Вектор am называется линейной комбинацией векторов a1,a2 , ,am 1 векторного пространства R, если
am 1a1 2a2 m 1am 1 ,
где i – действительные числа i 1,m 1.
Векторы a1,a2 , am векторного пространства R называются линей но зависимыми, если существуют такие числа 1, 2, , m , не равные одновременно нулю, что
1a1 2a2 mam 0 .
В противном случае векторы a1,a2 , ,am называются линейно
независимыми.
Если векторы a1,a2 , ,am линейно зависимы, то по крайней мере один из них может быть представлен в виде линейной комбинации остальных векторов.
Линейное пространство R называется n9мерным, если в нем существуют n линейно независимых векторов, а любые n 1 векторов
уже являются зависимыми. Число n называется размерностью про
странства R.
Совокупность n линейно независимых векторов n9мерного про9 странства R называется базисом.
30
