
1459
.pdf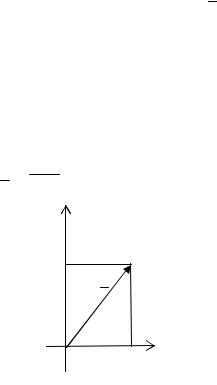
Модуль 3. ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.
НЕОПРЕДЕЛЕННЫЙ И ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
3.1. Элементы теории функций комплексного переменного
Комплексным числом z называется упорядоченная пара чисел x, y , x Re z – действительная, y Im z – мнимая части. Запись числа z в виде z x iy называется алгебраической формой комплексного числа. Символ i называется мнимой единицей ( i2 1).
Если x 0 , |
то число |
0 iy iy называется чисто мнимым, если |
y 0 , то число |
x i 0 x |
отождествляется с действительным числом |
x . Множество R действительных чисел является подмножеством множества C всех комплексных чисел ( R C ).
Два комплексных числа z1 x1 iy1 и z2 x2 iy2 называются рав ными тогда и только тогда, когда равны их действительные и мнимые части, то есть z1 z2 при x1 x2 и y1 y2 . В частности, комплексное число z x iy равно нулю тогда и только тогда, когда x y 0 .
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Два комплексных числа z x iy и z x iy , отличающиеся толь ко знаком мнимой части называются сопряженными.
Всякое комплексное |
число z x iy можно изобразить точкой |
M x, y плоскости xOy . |
Плоскость, на которой изображаются ком |
плексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной осью, а ось ординат – мнимой.
Комплексное число z x iy можно изобразить и с помощью радиус вектора r OM x, y .
y
M
r
O x
121
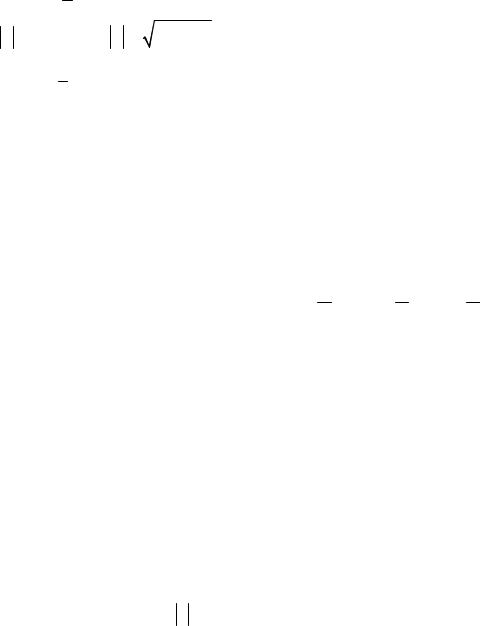
Длина вектора r называется модулем комплексного числа z, обозначается z или r ; r z x2 y2 .
Величина угла между положительным направлением действитель ной оси и вектором r , изображающим комплексное число, называется аргументом этого числа, обозначается Arg z или . Аргумент ком плексного числа z 0 не определен. Аргумент комплексного числа z 0 – величина многозначная и определяется с точностью до сла гаемого 2 k : Arg z arg z 2 k , где arg z – главное значение аргумента,
заключенное в промежутке , .
Запись числа z в виде z r cos i sin называется тригоно$ метрической формой комплексного числа.
Аргумент определяется из формул cos xr , sin yr , tg xy .
Иногда в качестве главного значения аргумента берут величину, при надлежащую промежутку 0,2 , тогда
|
y |
, при x 0, y 0 (для внутренних точек I четв.); |
|||
arctg |
|
||||
x |
|||||
|
|
|
|
||
y |
|
|
|
||
|
|
|
|
||
arg z arctg |
|
2 , при x |
0, y 0 |
(для внутренних точек IV четв.); |
|
x |
|||||
|
|
|
|
||
|
y |
, при x 0 (для внутренних точек II,Ш четв.). |
|||
arctg |
|
||||
x |
|||||
|
|
|
|
||
Используя формулу Эйлера ei cos i sin , комплексное число z можно записать и, в так называемой, показательной (или экспонен циальной) форме: z r i , где r z – модуль комплексного числа, а угол Arg z arg z 2 k .
Суммой двух комплексных чисел z1 x1 iy1 и z2 x2 iy2 назы вается число, определяемое равенством
x1 iy1 x2 iy2 x1 x2 i y1 y2 .
Вычитание определяется как действие, обратное сложению:
x1 iy1 x2 iy2 x1 x2 i y1 y2 .
Произведением комплексных чисел z1 x1 iy1 и z2 x2 iy2 назы вается комплексное число, определяемое равенством:
x1 iy1 x2 iy2 x1x2 y1y2 i x1y2 y1x2 .
122

Получается путем перемножения двучленов x1 iy1 и x2 iy2 с учетом i2 1:
x1 iy1 x2 iy2 x1x2 iy1x2 iy2x1 i2y1y2 x1x2 y1y2 i x1y2 y1x2 .
Частное двух комплексных чисел находят путем умножения числи теля и знаменателя на число, сопряженное знаменателю (избавляются от мнимости в знаменателе):
|
x1 iy1 |
|
x1 iy1 |
x2 iy2 |
|
|
x1x2 y1y1 |
i |
y1x2 x1y2 |
, п р и z |
|
0 . |
|||||||||||
|
|
|
x |
|
iy |
|
|
|
|
||||||||||||||
|
x |
2 |
iy |
|
x |
2 |
iy |
2 |
|
x2 y2 |
x2 |
y2 |
|
2 |
|
|
|||||||
|
|
2 |
|
|
2 |
|
2 |
|
|
|
2 |
2 |
|
2 |
2 |
|
|
|
|
|
|||
|
|
При |
умножении |
комплексных |
чисел |
z1 r1 cos 1 i sin 1 |
и |
||||||||||||||||
z2 r2 cos 2 i sin 2 , |
заданных |
в |
тригонометрической |
форме |
их |
||||||||||||||||||
модули перемножаются, а аргументы складываются, то есть
z1 z2 r1 cos 1 i sin 1 r2 cos 2 i sin 2 = r1 r2 cos 1 2 i sin 1 2 .
Откуда следует формула Муавра для возведения комплексных чисел в натуральную степень:
zn r cos i sin n r n cos n i sin n .
Деление комплексных чисел, заданных в тригонометрической форме осуществляется по формуле:
z1 r1 (cos 1 2 i sin 1 2 ), z2 r2
то есть, модули делятся, а аргументы вычитаются.
Корень n $й степени из комплексного числа z определяется как комплексное число w , удовлетворяющее равенству wn z :
|
n z w , |
где wn z . |
|
Если z r cos i sin , а |
w cos i sin , то, по определению |
корня и формуле Муавра, получаем
z wn n cos n i sin n r cos i sin .
Отсюда n r,n 2 k,k Z . То есть |
2 k |
и n r . |
|
n |
|
123
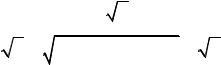
Поэтому равенство n z w принимает вид: |
|
|
|
|||
|
|
2 k |
i sin |
2 k |
||
n z n r cos i sin n r cos |
|
n |
n |
, |
||
|
|
|
|
|
||
где k 0,1,2, , n 1. |
|
|
|
|
|
|
Любое комплексное число z 0 имеет ровно n различных корней n й |
||||||
степени. |
|
|
|
|
|
|
Комплексные функции действительного переменного |
|
|
||||
Если каждому значению действительного параметра |
t соответ |
|||||
ствует определенное комплексное число |
|
|
|
|
|
|
|
z t x t iy t , |
|
|
|
|
|
где x t и y t – |
функции, принимающие действительные значения, то |
|||||
|
z t называется комплексной функцией действитель |
|||||
|
ного переменного. |
|
|
|
|
|
Параметр t |
изменяется в некотором конечном или бесконечном |
|||||
интервале. |
|
|
|
|
|
|
Годографом функции z t называется линия с параметрическими |
||||||
уравнениями x x t и y y t . |
|
|
|
|
|
|
Непрерывность комплексной функции |
z t |
эквивалентна непре |
||||
рывность ее действительной и мнимой частей x t и y t .
Производная комплексной функции действительного переменного определяется как предел отношения приращения функцииz z t t z t к приращению независимой переменной t :
|
|
z t |
lim |
z . |
|
|
|
|
|
t 0 |
t |
|
|
Производная |
z t является |
комплексной |
функцией. |
Геометри |
||
чески, вектор, |
изображающий комплексное число z t0 параллелен |
|||||
касательной |
к |
годографу функции |
z t , проведенной |
в точке, |
||
соответствующей значению параметра t0 . |
|
|
||||
Справедливо |
z t x t iy t , то есть комплексную функцию |
|||||
действительного переменного z t x t iy t |
можно дифференциро |
|||||
вать как обыкновенную сумму, считая i просто постоянным. Разу меется, это правило приобретает смысл только после введенных выше определений. Все правила дифференцирования действительных функ ций без всяких изменений переносятся на комплексные функции.
124

Показательная функция с мнимым показателем степени опреде ляется как комплексная функция
eit cost i sin t ,
где t может принимать любые действительные значения.
Приведенная формула носит название формулы Эйлера. Правая часть формулы представляет собой тригонометрическую форму записи комплексного числа с модулем, равным 1, и аргументом, равным t :
eit 1, Argeit t .
Годографом функции z eit служит единичная окружность. Комплексная функция eit дифференцируется так же, как если бы i
было просто постоянным числом:
eit sin t i cost i cost i sin t ieit .
Заменив в формуле Эйлера t на t , получим e it cost i sin t
( eit и e it – комплексно сопряженные выражения). Тригонометрические функции cost и sin t можно представить
через показательные функции действительного переменного в виде
|
eit e it |
eit e it |
||
cost |
|
, sin t |
|
. |
2 |
|
|||
|
|
2i |
||
Эти формулы также называются формулами Эйлера.
Решение уравнений
Уравнение Pn x 0 , где Pn x a0 xn a1xn 1 an , называется алгебраическим уравнением n ой степени; коэффициенты a0 ,a1, ,an – действительные или комплексные числа, a0 0 .
Основная теорема высшей алгебры. Всякое алгебраическое урав нение степени n 0 имеет хотя бы один корень, действительный или комплексный.
Справедливо Pn x x Qn 1 x R , где Qn 1 x – многочленn 1 й степени. Если – корень многочлена Pn x , то R P 0 и
Pn x x Qn 1 x .
125
Теорема Безу. Остаток от деления многочлена P x на двучлен
x равен значению этого многочлена при x .
Из предыдущего следует разложение многочлена Pn x на линей ные множители:
|
Pn x ao x x1 k1 x x2 k2 x xr kr , |
|
где k1,k2, ,kr – |
кратности корней x1, x2, , xr соответственно; |
|
r – |
число различных корней; k1 k2 kr |
n . |
Таким образом, алгебраическое уравнение n $й степени имеет n кор$ ней, если каждый корень считать столько раз какова его кратность.
Если все коэффициенты a0 ,a1, ,an – действительные числа, то комплексные корни уравнения (если они есть) попарно сопряжены. Тогда любой многочлен нечетной степени имеет хотя бы один действи$ тельный корень. Для произведения комплексно сопряженных корней справедливо:
x i |
x i |
x2 px q , |
||
|
|
|
|
|
|
p 2 , |
q 2 2, |
p2 4q 0 . |
|
Откуда следует возможность разложения многочлена с действи тельными коэффициентами в виде:
Pn x a0 x x1 k1 x xs ks x2 p1x q1 l1 x2 pt x qt lt ,
где k1 ks 2 l1 lt n , ki – кратности действительных корней, l j – кратности комплексно сопряженных корней.
Не существует формул, пользуясь которыми можно было бы при помощи конечного числа алгебраических действий выразить корни через коэффициенты таких уравнений (решить уравнение в радика лах), если степень n 5. При n 3 и n 4 соответственно исполь зуются формулы Кардано и Феррари. При n 1 и n 2 получим соот ветственно линейное или квадратное уравнение.
126

3.2. Неопределенный и определенный интегралы
Неопределенный интеграл
Первообразной для функции f x на данном интервале называется такая функция F x , производная которой равна f x (для всех x из
данного интервала):
F x f x .
Непрерывная в интервале a,b функция f x имеет бесконечное множество первообразных на a,b . Если F x – одна из них, то всякая другая имеет вид F x C , где C – постоянная величина.
Неопределенным интегралом от функции f x называется сово купность F x C всех ее первообразных:
f x dx F x C ;
f x dx называется подынтегральным выражением, f x – подын
тегральной функцией, дифференциал dx указывает на то, что инте грирование ведется по переменной x.
Правила интегрирования (свойства неопределенного интеграла)
1.d f x dx f x dx.
2.dF x F x C .
3.f x dx f x .
4.af x dx a f x dx , где a – постоянная.
5.( f1 x f2 x )dx f1 x dx f2 x dx .
6.Если f x dx F x C и u x , то f u du F u C .
Таблица интегралов
1. 0dx C.
x1
2.x dx 1 C
3.x 1dx dxx ln
1.
x C, x 0; 0 a,b .
127
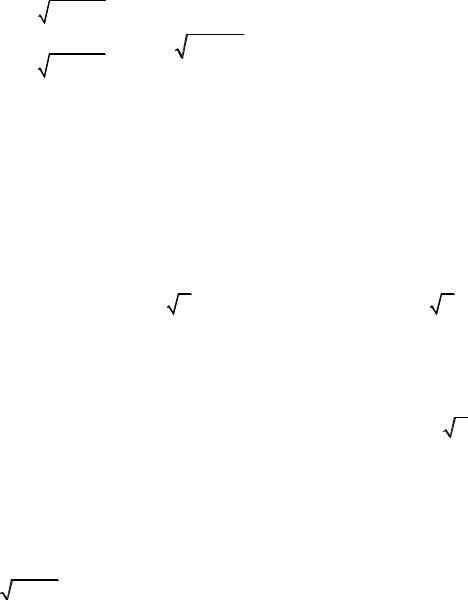
4. ax dx |
ax |
C, a 0, a 1. |
|
ln a |
|||
|
|
5.ex dx ex C.
6.sin xdx cos x C.
7.cos xdx sin x C.
8. |
|
|
|
|
dx |
|
tg x C на (a,b), где |
|
dx |
|
непрерывна. |
|
||||||||||||||||||||||||||||||||||||
cos2 x |
|
cos2 x |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
9. |
|
|
|
|
dx |
|
ctg x C на (a,b), где |
|
|
|
dx |
|
|
непрерывна. |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
sin2 x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 x |
|
|
|
|||||||||||||
10. |
|
|
|
|
dx |
|
|
|
|
arcsin |
x |
|
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
a2 x2 |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
11. |
|
|
|
|
dx |
|
|
|
|
ln |
|
x |
|
|
x2 a2 |
|
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
x2 a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
12. |
|
|
|
|
dx |
|
|
|
arctg |
x |
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
a |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
13. |
|
|
|
|
|
dx |
|
|
|
1 |
ln |
|
a x |
|
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
a |
2 |
x |
2 |
|
2a |
a |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Методы интегрирования |
|
|
|
||||||||||||||||||||||||||
1. Непосредственное интегрирование |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2x2 3sin x 5 |
|
x dx 2x2dx 3sin xdx 5 |
xdx |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x2dx 3 sin xdx 5 x |
|
dx |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
10 |
|
|
||||||||
|
2 |
3 |
cos x |
|
|
|
2 |
C |
|
x3 |
3cos x |
|
x C. |
|||||||||||||||||||||||||||||||||||
|
|
5 |
|
|
|
|
|
x |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Преобразование интеграла к табличному при помощи внесения некоторой функции под знак дифференциала
Пример.
|
1 |
|
1 |
|
2 |
3 |
|
|||
|
3x 1dx 3x 1 |
|
|
d 3x 1 |
3x 1 |
|
C . |
|||
2 |
2 |
|||||||||
3 |
9 |
|||||||||
|
|
|
|
|
|
|
||||
128

Интегралы вида |
|
|
dx |
|
, |
|
|
|
dx |
|
вычисляются |
при |
||||
|
2 |
|
|
|
|
|
|
|
||||||||
|
ax |
|
bx c |
|
ax2 bx c |
|
|
|
|
|||||||
помощи выделения полного квадрата: |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
b 2 |
|
b2 |
|
|
|
|
|
|
||
ax2 bx c a x |
|
|
|
|
c . |
|
|
|
|
|||||||
|
4a |
|
|
|
|
|||||||||||
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
После этого, заменив dx на равный ему дифференциал |
d x |
|
|
, |
||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
используют одну из четырех последних формул, приведенных выше в таблице основных интегралов.
dx
Пример. Вычислить x2 4x 13 .
Так как x2 4x 13 x 2 2 9, то, в силу dx d x 2 , имеем:
|
dx |
|
d x 2 |
|
1 |
arctg |
x 2 |
C . |
|
|
|
|
|||||
x2 4x 13 |
x 2 2 32 |
3 |
3 |
2. Метод замены переменной (подстановки)
Замена переменной (иногда называемая также подстановкой) состоит в том, что вместо переменной x в подынтегральное выражение f x dx вводится функция x t :
f x dx f t t dt.
Функцию (t) следует выбирать так, чтобы можно было вычислить неопределенный интеграл, стоящий в правой части последнего равенства.
Пример. Вычислить x |
x 2dx . |
|
|
|
|
|
|
|
|
|
|||||
Обозначим x 2 t . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда x 2 t2, |
x t2 |
2, |
dx 2tdt . Далее имеем |
|
|||||||||||
|
x |
x 2dx t2 |
2 t2tdt |
|
|
|
|
||||||||
2 t4 2t |
2 dt |
|
|
|
|
5 |
|
|
3 |
|
|||||
2 |
t5 |
4 |
t3 C |
|
2 |
x 2 |
|
|
4 |
x 2 |
|
C. |
|||
|
2 |
2 |
|||||||||||||
5 |
3 |
5 |
3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
129

3. Интегрирование по частям
Производится по формуле
udv uv vdu ,
где u(x), v(x) – непрерывно дифференцируемые функции. Подынтегральное выражение разбивается на две части, одну из
которых принимают за u, а другую – за dv так, чтобы интеграл vdu
вычислялся проще, чем исходный.
Метод позволяет вычислять интегралы видов:
I. P x e x dx, |
P x cos x dx, |
P x sin x dx ; |
II. P x ln xdx, |
P x arcsin xdx, |
P x arctgxdx , |
где P x – многочлен.
Для интегралов типа I в формуле интегрирования по частям прини мается P x u , а для интегралов типа II – P x dx dv .
Пример. Вычислить x ln xdx .
Введя u ln x, dv xdx , |
получим |
|
du |
1 |
dx,v xdx |
x2 |
. Откуда |
|||||||||
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||
x ln xdx |
x2 |
ln x |
1 |
|
x2dx |
|
x2 |
ln x |
1 |
x2 |
C . |
|
|
|||
|
2 |
x |
|
4 |
|
|
||||||||||
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|||||
Интегрирование рациональных функций разложением на простейшие дроби
Рассмотрим отношение двух алгебраических многочленов (назы
вается рациональной функцией или рациональной дробью)
f x Pm x , Qn x
Pm x b0 b1x bm xm ,
Qn x a0 a1x an xn ,
где bj , ai – действительные числа, i 0,n, j 0,m ; bm,an 0, m 0, n 1.
Будем полагать m n .
130
