1408

предложил внести изменения в планетарную модель атома. Эти изменения он сформулировал в виде двух постулатов и правила квантования орбит.

Первый постулат Бора: в атоме существует определённый набор устойчивых, стационарных орбит, двигаясь по которым, электрон не излучает электромагнитную энергию.

Правило квантования орбит: на стационарной орбите момент импульса электрона квантуется (кратен постоянной Планка)

me nrn nh n , 2

где n – номер орбиты электрона (целое число, отличное от нуля); rn – радиус т-й орбиты; n – скорость электрона на этой орбите; me – масса электрона; me nrn – момент импульса электрона на этой орбите; h – по-

Второй постулат Бора: атом излучает или поглощает квант электромагнитной энергии при переходе электрона с одной стационарной орбиты на другую.

Находясь на некоторой из таких орбит с номером n , электрон имеет определённую энергию En. Он может перейти на орбиту, имеющую номер m, с большей энергией Em если атомом будет поглощён фотон с энергией, равной Em–En. И наоборот, атом излучает световой квант (фотон) с такой же энергией, если электрон переходит с более удалённой орбиты на орбиту, расположенную ближе к ядру.

Энергия излучённого фотона равна разности энергий стационарных состояний:

hν Em En.

Эти постулаты легли в основу боровской модели атома.

Модель Бора не была квантовой в чистом виде. Наряду с неклассическими, квантовыми представлениями в ней использовались и типично классические (понятие траектории частицы, второй закон Ньютона). Это и ограничило возможность применения модели Бора только простейшей системой – атомом водорода. Тем не менее, успех модели Бора стал ещё одним свидетельством правильности предположения о дискретном, квантовом характере процессов, в которых участвуют микрочастицы. В 1922 г. Бор получил Нобелевскую премию по физике «За заслуги в изучении строения атома», а предложенная им модель атома получила название модели Резерфорда – Бора.

В новых взглядах на процессы в микромире принципиально важной стала идея о возможности изменений физических величин, характеризую-

71

щих микрообъект, лишь в рамках определённого набора «разрешённых» значений этих величин. Постоянную Планка стали рассматривать как величину, определяющую масштаб изменения квантующихся характеристик микрообъектов, как своеобразную порцию воздействия в микромире. Через неё выражаются все характеристики, которыми обмениваются взаимодействующие объекты, если хотя бы один из них относится к микромиру. Поэтому часто постоянную Планка называют ещё квантом действия.

Таким образом, непрерывное изменение физических величин, воспринимавшееся в классической физике как само собой разумеющееся, оказалось неприемлемым при описании микрообъектов.

В классической физике нет принципиального различия между малыми объектами и большими – отсутствует критерий такого различия. С развитием концепции квантования этот критерий появился. Он связан с квантом действия: малые воздействия – это те, которые по порядку величины сравнимы с квантом действия h. Соответственно, к малым объектам относят те, которые реагируют на малые воздействия.

2.2. Спектр атома водорода

Внутреннее состояние атома изучать непосредственно невозможно из-за малости его размеров. Структура атома проявляется только косвенно

вявлениях, связанных с его внутренним строением. К числу этих явлений относится излучение.

При изучении излучения элементов ученым удалось установить общие закономерности в характере спектров и найти ряд эмпирических законов, которым они подчиняются. Было установлено, что спектральные линии всех элементов можно разбить на ряд серий. Структуры соответствующих серий, относящихся к различным химическим элементам, схожи между собой. В пределах одной серии расположение спектральных линий имеет определенный порядок.

Наиболее простым атомом является атом водорода. Он содержит единственный электрон. Ядром атома является протон – положительно заряженная частица, заряд которой равен модулю заряда электрона, а масса

в1836 раз превышает массу электрона. В начале XIX века были открыты дискретные спектральные линии в видимой части спектра испускания атома водорода. Впоследствии закономерности, которым подчиняются длины волн (или частоты) линейчатого спектра атома водорода, были изучены количественно. В 1885 г. швейцарский физик И. Бальмер пред-

72

ложил эмпирическую формулу, описывающую спектральные линии в видимой части спектра атома водорода:

R 212 n12 ,

где частота; R постоянная Ридберга ( R 3,29 1015 с-1); n 3, 4, 5…

Совокупность спектральных линий атома водорода в видимой части спектра, соответствующих разным значениям n , называется серией Баль-

мера.

Вначале XX века аналогичные серии спектральных линий были открыты в других частях спектра водорода.

Вультрафиолетовой части обнаружена серия Лаймана

Для всех линий спектра атома водорода записывают обобщенную

формулу Бальмера

R m12 n12 ,

где m номер серии ( m 1, 2, 3, 4…); n номер отдельной линии данной серии ( n m 1, m 2 ….).

Сериальные формулы свидетельствуют о существовании физических закономерностей в спектре атома водорода, объяснить которые с помощью классической физики невозможно.

73

2.3. Комбинационный принцип Ритца

Аналогичные спектральные линии имеются не только у атома водорода, а, например, и у щелочных металлов. Расположение спектральных линий у них определяется формулой, аналогичной формуле Бальмера. Частота, соответствующая какой-либо спектральной линии этой серии, является разностью двух величин, одна из которых зависит от номера m серии и постоянная для всех линий данной серии, а другая определяется номером n линии в этой серии. Такая закономерность объясняет, что

частота некоторой спектральной линии часто оказывается равной сумме частот, соответствующих двум другим линиям спектра.

Эта закономерность была установлена экспериментально Ритцем и названа комбинационным принципом, который является основой всей современной спектроскопии.

Комбинационный принцип Ритца: Для каждого атома возможно найти последовательность чисел, называемых спектральными термами, таких, что частоты всех спектральных линий этого атома будут выражаться в виде двух каких-либо спектральных термов:

T1 m T2 n .

Справедливость этого принципа подтверждается многочисленными экспериментальными данными. Обоснование этого принципа связано со строением атома, с процессами, происходящими внутри атома при излучении волн с частотой, соответствующей какой-либо спектральной линии. И только теория Бора, выдвинутая им в 1913 г., выявила значение спектральных законов и показала, что эти законы отражают квантовый характер внутриатомной структуры.

2.4. Энергетический спектр атома водорода

Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем, состоящих из ядра с зарядом Ze и одного электрона (например, ионы He+, Li2+).

Следуя Бору, рассмотрим движение электрона в водородоподобной системе, ограничиваясь круговыми стационарными орбитами. Решая совместно уравнение

предложенное Резерфордом, и уравнение me nrn n ,

74

где n 1, 2, 3, ... .

Из формулы (2.2) следует, что радиусы орбит растут пропорционально квадратам целых чисел.

Для атома водорода ( Z 1) радиус первой орбиты электрона (при n 1), называемый первым боровским радиусом, равен

r1 2 4 2 0 0,528 10 10 м mee

Радиус n-й стационарной орбиты

rn r1n2 .

Так как радиусы стационарных орбит измерить невозможно, то для проверки теории необходимо обратиться к таким величинам, которые могут быть измерены экспериментально. Одной из таких величин является энергия, излучаемая и поглощаемая атомом.

Полная энергия электрона E в водородоподобной системе складывается из его кинетической энергии

Eк me2 2

и потенциальной энергии в электростатическом поле ядра

где n 1, 2, 3, ... .

Полная энергия электрона в атоме отрицательна, так как отрицательна потенциальная энергия электростатического взаимодействия электрона с ядром (электрон в атоме находится в связанном состоянии). С ростом номера орбиты полная энергия электрона в атоме возрастает, причем

75

величина ее может принимать только дозволенные дискретные значения, удовлетворяющие (2.3).

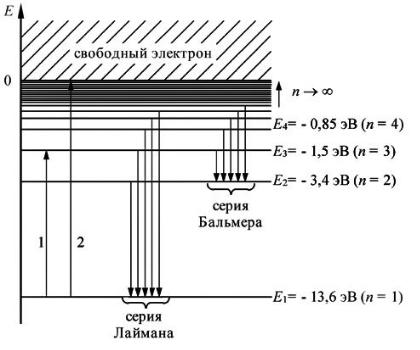
Из формулы (2.3) следует, что энергетические состояния атома водорода образуют последовательность энергетических уровней, изменяющихся в зависимости от значения n . Целое число n в выражении (2.3), определяющее энергетические уровни атома, называется главным квантовым числом. Энергетическое состояние с n 1 является основным (нормальным) состоянием; состояния с n >1 являются возбужденными. Для каждого значения n формуле (2.3), можно рассчитать энергетические уровни, схематически представленные на рис. 2.1.

Рис. 2.1. Энергетический спектр электрона в атоме водорода

При n 1 энергия атома водорода минимальна ( E1 13,55 эВ). При n энергия становится максимальной ( E 0 ). Следовательно, значение E 0 соответствует ионизации атома (отрыву от него электрона).

Переход электрона с одного уровня на другой на рис. 2.1 изображен соответствующей стрелкой, начало и конец которой указывают энергетические уровни, между которыми происходит переход.

Примеры решения задач

Пример 1. Вычислите длину волны света, излучаемого атомом водорода при переходе электрона с пятого энергетического уровня на третий. Определите энергию, массу и количество движения испускаемого фотона.

76

где R постоянная Ридберга ( R 1,1 107 м); m номер

уровня, на который переходит электрон; n номер уровня, с которого переходит электрон.

Из формулы (1) выразим длину волны

77

Пример 2. Найдите значение кинетической, потенциальной и полной энергии электрона на первой боровской орбите в атоме водорода.

Е?

атакже тем, что центростремительная сила равна силе электростатического притяжения между электроном и ядром

Выражая r из формулы (1) и подставляя это выражение в формулу (2), получаем:

Чтобы определить радиусы допустимых орбит, подставим выражение

(3) в (2), тогда

Зная зависимости и r от квантового числа n , получим выражения для кинетической, потенциальной и полной энергии электрона в атоме водорода

Знак «–» означает, что электрон находится в связанном состоянии.

78

Пример 3. Определите период обращения электрона на первой боровской орбите в атоме водорода и его угловую скорость.

найдем зависимость периода T обращения электрона и его угловой скорости от главного квантового числа n :

Пример 4. Электрон в атоме водорода находится в основном стационарном состоянии. Сравните энергию ионизации атома водорода с кинетической энергией электрона, вращающегося вокруг ядра (учесть, что электрон движется по круговой орбите).

79

зарядовое число; e элементарный заряд ( e 1,6 10 19 Кл); 0 электриче-

ская постоянная ( 0 8,85 10 12 Ф/м).

С другой стороны, согласно первому постулату Бора

где n главное квантовое число.

Из уравнений (1) и (2) следует, что n Ze2 . 2 0nh

Кинетическая энергия электрона равна

где R – постоянная Ридберга; n и m – главные квантовые числа, соответствующие энергетическим уровням, между которыми осуществляется переход.

Поэтому

Wион hcR n12 m12 ,

80