
1408
.pdf
где h – постоянная Планка; c – скорость света в вакууме; 1 – длина
волны рассеянного света.
Длина волны рассеянного света равна
1 2 h sin2 , m0c 2
где – длина волны падающего света; h – постоянная Планка; m0 – масса покоящегося электрона; – угол рассеяния.
Длина световой волны до рассеяния
hc .
Поэтому
|
|
|
|
|
|
|
|
|
|
hc |
|
|
|
|
|
|
с |
|
|
|
. |
|
|
|
|
|
|
hc |
2 |
h |
sin2 |
с |
2 |
1 |
sin2 |
|
|||||||||
|
|
|
|
|
|
|
m c |
|
m c |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
3 108 |
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
. 3,84 10 |
|
Дж. |
||||||||
|
3 108 |
2 |
|
|
1 |
|
|
|
sin |
2 120 |
|
|||||||||||
|
1,28 10 |
13 |
9,1 10 |
31 |
3 |
8 |
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|||||||
Изменение энергии электрона
W ' .
W 12,8 3,84 10 14 8,96 10 14 Дж.
Ответ: 3,84 10 14 Дж, W 8,96 10 14 Дж.
Пример 3. Угол рассеяния фотона с энергией 1,2 МэВ на свобод-
ном электроне 60 . Найдите: 1) длину волны рассеянного фотона; 2) энергию и импульс электрона отдачи. Кинетической энергией электрона до соударения пренебречь.
Дано: |
|
|
Решение |
|||
1,2МэВ 1,92 10 13 Дж |
Изменение длины волны фотона при |
|||||
600 |
|
комптоновском рассеянии |
||||
|
|
|
h |
(1 cos ) 1 cos , (1) |
||
? ; Ек,e ? ; |
pe ? |
|||||
m c |
||||||
|
|
0 |
|
|
||
|
|
где и длины волн падающего и рас- |
||||
|
|
|
|
h постоянная Планка |
||
|
|
сеянного фотонов; |
||||
|
|
( h 6,63 10 34 Дж с); |
с скорость света в |
|||
|
|
вакууме; 2,43 10 12 м – комптоновская |
||||
|
|
длина волны; угол рассеяния. |
||||
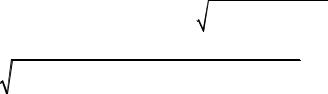
На рис.1.11 |
p и p импульсы падающего и рассеянного фотонов. |
|||||
61
Из формулы (1) находим
1 cos .
Выражая через энергию фотона
hc ,
получаем
hc |
1 cos . (2) |
|
|
6,63 10 34 3 108 2,43 10 12 1 0,5 2,25 10 12 м. 1,92 10 13
По закону сохранения энергии энергия электрона отдачи
Ек,e .
Выразим изменение длины волны через изменение частоты:
|
|
|
|
|
|
|
|
|
|
с |
|
|
с |
|
|
с |
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
С учетом (1) можно написать: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 cos . |
|
|
|
|
|
(3) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
m c2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Умножая выражение (3) |
на |
|
|
|
h |
и учитывая, |
что |
h , |
|
|
|
||||||||||||||||||
|
|
|
|
h , |
||||||||||||||||||||||||||
m0c |
2 |
E0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
, Ек,e , получаем |
|
|
|
|
2 1 cos |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
Е |
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
E0 1 cos |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
к,e |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
E 0,551 МэВ 0,82 10 13 |
Дж – энергия покоя электрона. |
|
|
|
|||||||||||||||||||||||||
|
|
0 |
|
|
|
|
1,22 1 0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Е |
|
|
|
|
0,648 |
МэВ 1,04 10 13 |
Дж. |
|
|
|
|
||||||||||||||||||
|
|
|
0,511 1,2 1 0,5 |
|
|
|
|
|||||||||||||||||||||||
|
|
к,e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Зная энергию электрона, находим его импульс: |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
Eк,e Eк,e 2E0 |
|
. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
p |
|
|
|
1,04 10 13 1,04 10 13 |
2 0,82 10 13 |
5,55 10 22 |
кг м/c. |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
e |
|
|
|
|
|
3 108 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Ответ: 2,25 10 12 |
м; Ек,e |
0,648 МэВ; |
pe 5,55 10 22 |
кг м/c. |
|||||||||||||||||||
62

Пример 4. В результате эффекта Комптона фотон при соударении с
электроном был рассеян на |
угол 900 . Энергия |
рассеянного |
фотона |
|||||||||||||||||||||||||||||||||
|
МэВ. Определите энергию фотона до рассеяния. |
|
|
|
||||||||||||||||||||||||||||||||
0,4 |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
Дано: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
||||||
|
МэВ 0,64 10 |
13 |
Дж |
|
|
Изменение |
длины |
волны |
фотона при |
|||||||||||||||||||||||||||
0,4 |
|
|
|
|
рассеянии на покоящемся электроне |
|
||||||||||||||||||||||||||||||
900 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
h |
|
sin2 , |
|
|||||||||||||||
? |
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 cos ) 2 |
(1) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
m c |
m c |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||
где |
m0 масса |
|
|
|
|
покоя |
|
|
электрона; |
|
h постоянная |
Планка |
||||||||||||||||||||||||
( h 6,63 10 34 Дж с); с скорость света в вакууме; угол рассеяния. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hc |
hc |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
(2) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где и длины волн падающего и рассеянного фотонов. |
|
|
||||||||||||||||||||||||||||||||||
|
Из формул (1) и (2) следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
hc |
|
hc |
2 |
|
h |
|
sin |
2 |
|
. |
|
|
|
|
|
|
(3) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m0c |
|
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Преобразуем правую часть формулы (3), умножив и разделив ее на с, и |
|||||||||||||||||||||||||||||||||||
выразим из нее величину энергии фотона до рассеяния: |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
m0 c2 |
|
|
|
|
|
|
|
|
|
|
|
E0 |
|
|
|
|
, |
|
|
|
||||||||||
|
|
|
m0 c |
2 |
|
|
|
|
2 |
|
|
E0 |
|
|
|
|
2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 sin |
|
2 |
|
|
|
2 sin |
|
2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где E 0,551МэВ 0,82 10 13 Дж – энергия покоя электрона. |
|
|
||||||||||||||||||||||||||||||||||
0 |
0,4 0,511 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,85 МэВ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0,511 2 0,4 sin |
2 |
|
90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: 1,85 МэВ.
Пример 5. Длина волны рентгеновского излучения, падающего на вещество со свободными электронами, 0,003 нм. Какую энергию
приобретает комптоновский электрон отдачи при рассеянии фотона под
углом 600 ? Дано:
0,003 нм 3 10 12 м
600
Ек,e ?
Решение Всоответствии сзакономсохраненияэнер-
гии, энергия электрона отдачи равна разности энергийпадающегоирассеянногофотонов
E |
hc |
|
hc |
|
hc |
, |
(1) |
|
|
|
|||||||
к,e |
|
|
|
|
|
63

где изменение длины волны фотона при рассеянии на покоящемся электроне.
|
|
|
|
|
|
|
|
|
h |
(1 cos ) . |
|
||
|
|
|
|
|
|
m c |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
6,63 10 34 |
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
-12 |
|
|
|||||
|
|
|
|
|
|
1 0,5 1,2 10 |
|
м. |
|
||||
9,1 10 |
31 |
3 |
8 |
|
|
||||||||
|
|
|
10 |
|
|
|
|
|
|
||||
Подставив значение в формулу (1), получим |
|
||||||||||||
E |
|
6,63 10 34 |
3 108 1,2 10 12 |
1,9 10 14 Дж. |
|
||||||||
3 10 12 3 10 12 1,2 10 12 |
|
||||||||||||
к,e |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: E |
1,9 10 14 Дж. |
|
|
|
|
|
|
|
|
|
|
|
|
к,e |
|
Задачи для самостоятельного решения
Средний уровень
1.В опыте Комптона наблюдалось рассеяние рентгеновских лучей на графите. Укажите верное утверждение.
1)энергия рассеянного фотона больше энергии падающего на графит фотона;
2)частоты падающего и рассеянного фотонов равны;
3)столкновение фотона с электроном в графите является упругим;
4)длина волны рассеянного фотона зависит от угла рассеяния .
2.Укажите верное утверждение. В опыте по рассеянию рентгеновских лучей на графите
1)фотон имеет импульс pф hc ;
2)фотон имеет энергию h и массу m hc2 ;
3)электрон отдачи до удара с фотоном имеет энергию W0 m0c2 , где m0 – масса покоя электрона;
4)фотон, столкнувшись с электроном, передает ему часть своей энергии и импульса.
3.Чему равна комптоновская длина волны?
1) |
h |
; |
2) |
h |
; |
3) |
h |
; |
4) |
2h |
. |
mc |
mc |
2mc |
|
||||||||
|
|
|
|
|
|
|
mc |
||||
4. В опыте Комптона k (1 cos ) . Укажите верное утверждение: 1) величина зависит от длины волны падающего фотона;
64
2)величина зависит от природы рассеивающего вещества;
3)значение k одинаково для графита и парафина;
4)возрастает с увеличением угла рассеяния .
5.Укажите закон сохранения энергии для системы «фотон – электрон»
вопыте Комптона.
|
m 2 |
|
|
|
h |
c |
m0c |
2 |
h |
c |
mc |
2 |
|
||
1) h h |
|
|
; |
|
2) |
|
|
|
|
; |
|||||
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
m 2 |
||||
|
|
2 |
|
|
|
|
c |
|
2 |
|
c |
|
|||
3) h h mc |
|
; |
|
4) |
h |
|
m0c |
|
h |
|
|
|
|
. |
|
|
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6. Рассматривая рассеяние рентгеновских лучей на графите, Комптон |
|||||||||||||||
при выводе формулы |
|
h |
(1 cos ) |
использовал законы со- |
|||||||||||
|
|||||||||||||||
m c |
|||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
хранения энергии и импульса. Какое утверждение не соответствует выводу этой формулы?
|
|
2 |
, где m |
m0 |
|
|
1) |
h h mc |
|
|
|
; |
|
|
1 |
2 |
||||
c2
2)pe pф pф, где pe – импульс электрона отдачи;
3)h m0c2 h mc2 , где m0 – масса покоя электрона;
4)pe m , pф hc , pф hc .
7. Чему равно изменение длины волны гамма-лучей при комптоновском рассеянии на свободных электронах на угол 3 ?
1) |
3h |
; |
2) |
h |
; |
3) |
h |
; |
4) |
2h |
. |
|
mc |
2mc |
mc |
||||||||||
2mc |
||||||||||||
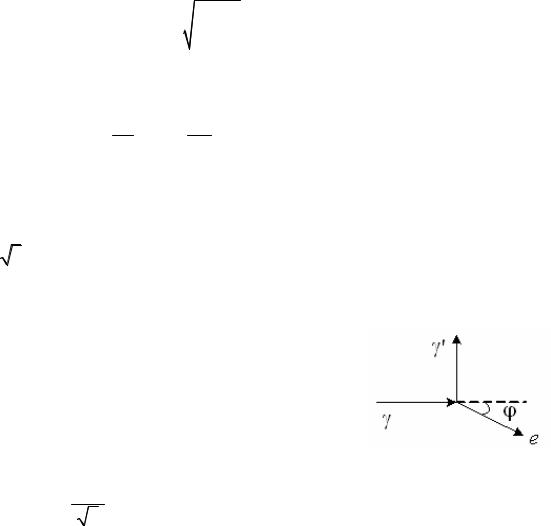
8. |
На рисунке показаны направления падаю- |
|
|
|
||||||||
щего фотона , рассеянного фотона и электрона
отдачи e . Угол рассеяния 90 . Направление движения электрона отдачи составляет с направлением падающего фотона угол 30 . Импульс
падающего фотона 10 7 . Чему равен импульс электрона отдачи?
Ответ: pe 2 p3ф .
65
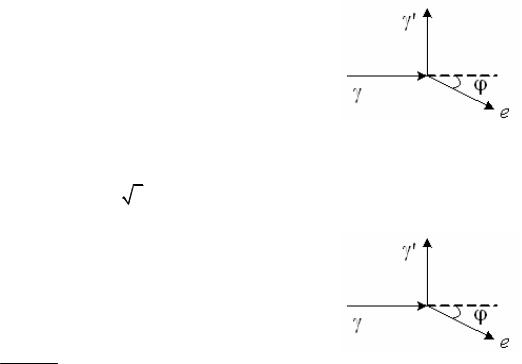
9. Эффект Комптона наблюдается на почти свободных электронах. На рисунке показаны направления падающего фотона , рассеянного фо-
тона и электрона отдачи e . Угол рассеяния 90 ,
направление движения электрона отдачи составляет с направлением падающего фотона угол
30 . Как изменится |
при рассеянии импульс |
фотона? |
|
Ответ: уменьшится в |
3 раз. |
10. При наблюдении эффекта Комптона угол рассеяния фотона на покоившемся свободном электроне равен 90 , направление движения электрона отдачи составляет с направлением падающего фотона угол 30 . Импульс рассеянного
МэВм с . Чему равен импульс электрона отдачи в тех же единицах?
Ответ: |
p 4 |
МэВ с |
. |
|
|||
|
e |
м |
|
|
|
||
Достаточный уровень
1. Рентгеновские лучи с длиной волны 70,8 пм испытывают комптоновское рассеяние на парафине. Найдите длину волны рентгеновских
лучей, рассеянных в направлениях: а) 2 ; б) .
Ответ: а) 73,22 пм; б) 75,6 пм.
2. Какова была длина волны 0 рентгеновского излучения, если при комптоновском рассеянии этого излучения графитом под углом
60 длина волны рассеянного излучения оказалась равной 25,4пм? Ответ: 24,2 пм.
3.Рентгеновские лучи с длиной волны 20 пм испытывают комптоновское рассеяние под углом 2 . Найдите изменение , длины
волны рентгеновских лучей при рассеянии, а также энергию We и импульс p электрона отдачи.
Ответ: 2,42 пм; We 6,6 кэВ; pe 4,4 10 23 кг м/c.
66
4. Гамма-излучение с длиной волны 2,7 пм испытывает комптоновское рассеяние. Во сколько раз длина волны излучения, рассеянного
под углом 180 к первоначальному направлению, больше длины волны падающего излучения?
Ответ: в 2,8 раз.
5.Найдите энергию фотона, у которого при центральном соударении с электроном длина волны возрастает в 1,5 раза. Какова при этом энергия электрона отдачи?
Ответ: 127 кэВ; We 42кэВ.
6.Фотон с длиной волны 4,86 пм рассеялся на первоначально покоившемся свободном электроне. Комптоновская длина волны для электрона
равна 2,43 10 12 м. Чему равно отношение максимально возможной длины волны рассеянного фотона к его первоначальной длине?
Ответ: max 2 .
7. При рассеянии фотона на свободном электроне кинетическая энергия отдачи электрона максимальна. Чему при этом равен угол рассеяния в градусах?
Ответ: 180 .
8. В явлении Комптона энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол рассеяния
равен 2 . Комптоновская длина волны электрона 2,43 10 12 м. Чему
равна длина волны рассеянного фотона?
Ответ: 4,8 10 12 м.
9. Угол рассеяния фотона в эффекте Комптона 2 , угол отдачи
электрона 30 . Определите энергию фотона до рассеяния. Ответ: 374 кэВ.
10. При комптоновском рассеянии энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол
рассеяния 2 . Найдите энергию и импульс p рассеянного фотона. Ответ: 0,26 МэВ; p 9,3 10 12 кг м/c.
67

11. Узкий пучок монохроматического рентгеновского излучения падает на рассеивающее вещество. При этом длины волн излучения, рассеянного
под углами 1 60 и 2 120 , отличаются друг от друга в 2 раза. Считая,
что рассеяние происходит на свободных электронах, найдите длину волны падающего излучения.
Ответ: 1,2 пм.
12. Длина волны гамма-лучей при комптоновском рассеянии на свободных электронах увеличилась на 2mch . Чему равен угол рассеяния в
градусах? Ответ: 60 .
13. Фотон с длиной волны 6 пм рассеялся под прямым углом на покоившемся свободном электроне. Найдите: а) частоту рассеянного фотона; б) кинетическую энергию электрона отдачи.
Ответ: 5,3 1020 рад/с; Eк,e 60 кэВ.
14. В результате комптоновского рассеяния электрон приобрел энергию We 0,5МэВ. Определите энергию падающего фотона, если длина
волны рассеянного фотона 0,025 нм. Ответ: 0,55 МэВ.
15. Фотон с импульсом 1,02 МэВ/с (с – скорость света) в результате
эффекта Комптона был рассеян на угол 30 . Определите импульс рассеянного фотона.
Ответ: p 4,3 10 22 кг м/c.
16. Фотон с энергией в 2 раза превышающей энергию покоя электрона, испытал лобовое столкновение с покоившимся свободным электроном. Найдите радиус кривизны траектории электрона отдачи в магнитном поле B 0,12 Тл. Предполагается, что электрон отдачи движется перпен-
дикулярно к направлению поля. Ответ: R 3,4 см.
17. Фотон с энергией 100 кэВ рассеивается на угол 60 . Какую кинетическую энергию приобретает электрон отдачи? На какой угол он отклоняется от рассеянного фотона?
Ответ: Eк,e 8,9 кэВ; 115 .
68
Контрольные вопросы
1.В чем заключается эффект Комптона?
2.Опишите установку Комптона.
3.От чего зависит величина изменения длины волны излучения при комптоновском рассеянии?
4.В чем заключалось противоречие между результатами опыта Комптона и классической теорией рассеяния волн?
5.Чем вызвано наличие в рассеянном рентгеновском излучении двух компонент?
6.Почему эффект Комптона наблюдается в опытах с рентгеновским излучением и не наблюдается в опытах с видимым или ультрафиолетовым излучением?
69
2.ОСНОВЫ ФИЗИКИ АТОМА
2.1.Боровская модель атома и концепция квантования
Первый шаг на пути создания квантовой теории атомов был сделан датским физиком Н. Бором (1885–1962 гг.). В 1913 г. Бор предложил модель атома водорода, в которой были использованы новые представления о квантовом характере излучения и поглощения света, о дискретности изменения физических характеристик микрообъектов. Он разработал эту модель на основе «планетарной» модели строения атома, предложенной в 1911 г. английским физиком Э. Резерфордом (1871–1937 гг.). Согласно «планетарной» (ядерной) модели, атом состоит из положительно заряженного ядра и электронов, вращающихся вокруг ядра в его электрическом поле. Название «планетарная» отражает очевидную аналогию атома с Солнечной системой, в которой планеты движутся по некоторым определенным орбитам вокруг массивного притягивающего центра – Солнца.
Планетарная модель атома оказалась противоречивой с точки зрения классической физики.
Во-первых, на основе этой модели нельзя было объяснить факт существования атома, его устойчивость. Ведь движение электронов по орбитам происходит с ускорением. Согласно законам классической электродинамики ускоренно движущийся заряд должен излучать электромагнитные волны определённой частоты. Следовательно, при движении электрона вокруг ядра атом должен непрерывно излучать энергию. Но уменьшение энергии приводит к уменьшению радиуса орбиты электрона. Следовательно, электрон должен двигаться по спирали, приближаясь к ядру. За ничтожно малое время электрон должен упасть на ядро, а атом – прекратить своё существование.
Во-вторых, с помощью планетарной модели невозможно было объяснить спектральные закономерности атомов. Действительно, при движении электрона по спирали с неизменной скоростью должна увеличиться круговая частота его вращения, а значит – непрерывно расти частота излучения, т.е. спектр излучения атома должен быть сплошным.
Таким образом, в модели Резерфорда атом является неустойчивой системой.
В действительности атомы весьма устойчивы и в невозбуждённом состоянии могут существовать неограниченно долго, совершенно не излучая электромагнитные волны. При этом, как показали эксперименты, они имеют не сплошные, а линейчатые спектры излучения.
Чтобы разрешить возникшие противоречия, Бор впервые заявил, что законы электромагнетизма неприменимы для исследования микромира, и
70
