
1408
.pdf
Достаточный уровень
1. Определите с помощью уравнения Шредингера энергию электрона атома водорода в состоянии r A 1 ar e r , где A, a и –
некоторые постоянные.
Ответ: E me4 8 2 , то есть уровень с главным квантовым числом n 2.
8 2 , то есть уровень с главным квантовым числом n 2.
2. Волновая функция электрона в основном состоянии атома водорода
имеет вид r Ae r r1 , где A – некоторая постоянная, r1 – первый
боровский радиус. Найдите:
а) наиболее вероятное расстояние электрона от ядра; б) среднее значение модуля кулоновской силы; в) среднее значение потенциальной энергии;
г) средний электростатический потенциал, создаваемый электроном в центре атома.
Ответ:
а) вероятность нахождения электрона на расстоянии r,r dr от ядра
d 2 r 4 r2dr . Из условия максимума функции |
d dr получим |
rвер r1;
б)  f
f  2e2
2e2 r12 ;
r12 ;
в) 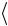 U
U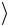 e2
e2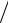 r1 ;
r1 ;
г) 0 e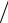 r12 .
r12 .
3. Частица массы m находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы равна l . Найдите возможные значения энергии частицы, имея в виду, что реализуются лишь такие состояния её движения, для которых в пределах данной ямы укладывается целое число дебройлевских полуволн.
Ответ: Eп 2 2 /2ml3 n2 , где n 1, 2,... .
4. Частица массы m движется в одномерном потенциальном поле U kx22 (гармонический осциллятор). Оцените с помощью соотношения не-
определенностейминимальновозможнуюэнергиючастицывтакомполе. Ответ: Emin , где – круговая частота осциллятора. Точный расчет
даёт 2 .
121
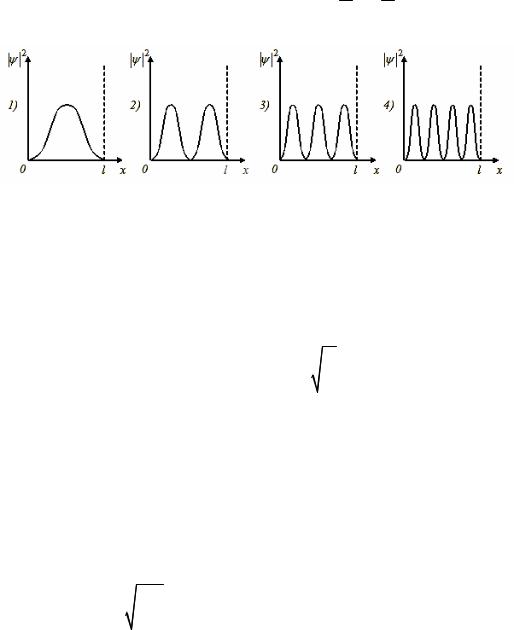
5. На рисунках схематически представлены графики распределения плотности вероятности обнаружения электрона по ширине одномерного потенциального ящика с бесконечно высокими стенками для состояний с различными значениями главного квантового числа n . Чему равно отношение вероятности обнаружить электрон на первом энергетическом уровне в левой половине ящика к вероятности обнаружить электрон на
четвертом энергетическом уровне в интервале от L4 до L2 ? Ответ: 2.
6. Частица массы m находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы равна l . Найдите нормированные волновые функции стационарных состояний частицы, взяв начало отсчета координаты x в середине ямы.
Ответ: Acos nxl , если n 1, 3, 5…;
|
nx |
, если n 2, 4, 6…, где |
A |
2 |
. |
|
Asin |
l |
|
l |
|||
|
|
|
|
|
||
7. Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы l такова, что энергетические уровни расположены весьма густо. Найдите плотность
уровней dNdE , то есть их число на единичный интервал энергии, в
зависимости от E . Вычислите dNdE для E 1,0 эВ, если l 1,0 см.
|
dN |
|
l |
|
m |
; при E 1эВ |
dN |
0,8 10 |
7 |
|
|
Ответ: |
|
|
|
|
|
|
dE |
|
уровней/эВ. |
||
dE |
|
2E |
|
||||||||
|
|
|
|
|
|
|
|
||||
8. Частица массы m находится в двухмерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками. Найдите:
а) возможныезначенияэнергиичастицы, еслистороныямыравны l1 и l2 ;
б) значения энергии частицы на первых четырех уровнях, если яма квадратная со стороной l .
122

Ответ: а) |
En n |
|
2 |
|
2 |
|
|
2 |
2 |
|
; б) 9,87 |
, 24,7 |
, 39,5, 49,4 |
единиц |
|
|
|
|
n1 |
n2 |
|
||||||||
|
1 2 |
2m |
|
|
l2 |
l2 |
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|||
2 ml2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. Волновая функция частицы массы m для основного состояния в
одномерном потенциальном поле U x |
kx2 |
имеет вид |
x Ae x2 , где |
|
|
||||
2 |
|
|
|
|
A – нормировочный коэффициент, – положительная |
постоянная. |
|||
Найдите с помощью уравнения Шредингера и энергию |
E частицы в |
|||
этом состоянии. |
|
|
||
Ответ: m 2 , E 2 , где k m . |
|
|
||
10. Собственные функции электрона в одномерном потенциальном
ящике с бесконечно высокими стенками имеют вид n x |
2 |
sin |
n |
x , |
L |
|
|||
|
|
L |
||
где L – ширина ящика, n – квантовое число, имеющее смысл номера
энергетического |
уровня. N |
– |
число узлов n функции на отрезке |
|||
0 |
x L и |
Nn 1 |
1,5 . Чему равно число n ? |
|||
|
||||||
|
|
Nn 1 |
|
|
|
|
|
Ответ: n 4. |
|
|
|
||
|
11. Частица |
находится |
в |
потенциальном ящике шириной L с |
||
бесконечно высокими стенками в определенном энергетическом состоянии
E с квантовым числом n . Известно, что En 1 4 . Чему в этом случае
n |
|
|
En 1 |
||
равно n ? |
||
|
||
Ответ: n 3 . |
|
12. Частица находится в одномерной бесконечно глубокой потенциальной яме, конфигурация которой показана на рисунке. Найдите уравнение, определяющее возможные значения энергии данной частицы в случае, когда её полная энергия E U0 .
Ответ: k2tgk1l1 k1tgk2 l2 l1 . Для очень больших значений E U0 ; k1 k2 .
123

13. Частица находится в одномерном симметричном потенциальном поле, вид которого показан на рисунке. Получите уравнение, определяющее спектр возможных значений полной энергии E частицы в области E U0 .
Ответ: tgk2l 2k1k2 .
k12 k22
14. Напишите волновое уравнение для электронов в молекуле водорода.
|
|
|
|
2m |
|
|
e |
2 |
|
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
|
Ответ: 1 2 |
E |
|
|
1 |
|
|
|
|
|
0 . |
|||||||||||
|
|
|
|
|
r2a |
r2b |
r12 |
|
|||||||||||||
|
|
|
|
|
|
4 0 r1a |
|
r1b |
|
|
|
rab |
|||||||||
15. Частица находится в трехмерном потенциальном ящике с абсо- |
|||||||||||||||||||||
лютно непрозрачными стенками. Ребра a1 , a2 , |
a3 . Определите возможные |
||||||||||||||||||||
значения энергии данной частицы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
h |
2 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: E |
|
n1 |
n2 |
|
n3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
a2 |
a2 |
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
16. Определите, при какой ширине потенциального ящика a дискретность энергии становится сравнимой с энергией теплового движения при температуре T .
Ответ: a h |
2n 1 . |
2 |
3kTm |
17. Электрон находится в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками. Определите вероятность W обнаружения электрона в средней трети ямы, если электрон находится в возбужденном состоянии ( n 3 ).
Ответ: W 1/ 3.
18. Известно, что нормированная собственная волновая функция, описывающая состояние электрона в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками, имеет вид
n x |
2 sin |
nx |
, где |
l ширина ямы. Определите среднее значение |
|
l |
l |
|
|
координаты электрона. Ответ: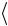 x
x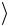 12 .
12 .
124
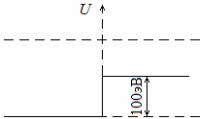
19. В одномерном потенциальном поле, профиль которого показан на рисунке ниже, движется в положительном направлении электрон с кинетической энергией 1 кэВ. Найдите, во сколько раз изменится дебройлевская длина волны его при переходе через скачок потенциала 100 В.
Ответ: 2 1,05.
1
20. Найдите для водородоподобных систем магнитный момент n ,
соответствующий движению электрона на n -й орбите, а также отношение магнитного момента к механическому n / Mn . Вычислите магнитный
момент электрона, находящегося на первой боровской орбите.
Ответ: me4 /h3 Z 2 /n3 2,07 1016 рад/с.
Контрольные вопросы
1.В чем заключается принципиальное отличие квантовомеханического описания состояния системы от классического описания?
2.Какие сведения о квантово-механической системе можно получить на основании решения уравнения Шредингера?
3.Квантуется ли энергия свободной частицы?
4.Какие физические характеристики системы определяются главным квантовым числом, орбитальным квантовым числом и магнитным квантовым числом?
5.Что такое спин электрона?
6.В чем физический смысл принципа Паули?
7.Какие частицы подчиняются принципу Паули? Какие не подчиняются?
8.Какими правилами определяется порядок заполнения электронных оболочек атомов?
9.Чем объясняется периодическая повторяемость химических свойств элементов?
125

3.ФИЗИКА АТОМНОГО ЯДРА
ИЭЛЕМЕНТАРНЫХ ЧАСТИЦ
3.1.Состав атомных ядер
Вопытах Резерфорда было установлено, что атом имеет ядро малых размеров и электронную оболочку. Ядро расположено в центре атома. Физические свойства атомного ядра определяются его зарядом и массой.
Электрический заряд q ядра атома равен произведению элементарного
электрического заряда e на порядковый номер Z химического элемента в таблице Д. И. Менделеева
q Ze.
Таким образом, порядковый номер химического элемента в таблице Д.И. Менделеева определяется числом положительных элементарных зарядов ядре любого атома химического элемента. В связи с этим порядковый номер элемента называется зарядовым числом.
Атомы, ядра которых обладают одинаковыми зарядами, имеют одинаковое строение электронных оболочек и поэтому химически не различимы.
Ядро – массивная частица. В нем сосредоточено 99,95 % массы атома. Изучение рассеяния альфа-частиц и других видов излучений на ядрах атомов различных химических элементов и другие исследования, показали что, многие атомные ядра имеют форму, близкую к сферической. Радиус
атомного ядра определяется приближенной формулой
R r0 A1 3 ,
3 ,
где r0 1,3 фм 1,3 10 15 м; A массовое число.
Так как радиус атомного ядра пропорционален корню кубическому из массы ядра, то объем ядра пропорционален его массе M в первой степени (и числу нуклонов в ядре)
V ~ R3 ~ A ~ M ,
поэтому плотность вещества во всех ядрах примерно одинакова. Поскольку M A 1,66 10 27 кг, то плотность ядерного вещества
|
М |
|
M |
|
|
1,66 10 27 A кг |
|
|
17 |
|
3 |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1,8 10 |
кг м |
|
|
V |
4 3 R |
3 |
4 / 3 (1,3 10 |
15 |
1 3 |
) |
3 |
м |
3 |
|
||||||
|
|
|
|
|
A |
|
|
|
|
|
|
|||||
После открытия нейтрона российский ученый Д.Д. Иваненко и немецкий физик В. Гейзенберг выдвинули гипотезу о протонно-нейтронном строении ядра. Согласно этой идеи, все ядра состоят из протонов и нейтронов.
126
Протон p имеет положительный заряд e , равный модулю заряда электрона. Масса протона в 1836 раз больше массы электрона и составляет
mp 1,6726231 10 27 |
кг 1,007276470 |
а.е.м. 938,27231 МэВ. |
|
Электрический |
заряд нейтрона |
n равен нулю, масса |
нейтрона |
m 1,6749286 10 27 |
кг 1,008664902 |
а.е.м. 939,56563 МэВ. |
Сравнение |
n |
|
|
|
массы нейтрона и протона показывает, что они различаются очень не значительно, менее чем на 0,2% . Однако важно отметить при этом, что
масса нейтрона превосходит массу протона более чем на две электронные массы.
В свободном состоянии нейтрон нестабилен (радиоактивен) – он самопроизвольно распадается, превращаясь в протон и испуская электрон
e и электронное антинейтрино e .
n p e e.
Период полураспада (т.е. время, за которое распадается половина первоначального количества нейтронов) равен примерно 12 мин.
Масса антинейтрино равна нулю. Поскольку масса нейтрона больше массы протона на величину 2,5me , то, масса нейтрона превышает сум-
марную массу частиц, фигурирующих в правой части данного уравнения, на 1,5me , т.е. на 0,77 МэВ. Эта энергия выделяется при распаде нейтрона в
виде кинетической энергии образующихся частиц.
Ядро простейшего атома – атома водорода – состоит из одной элементарной частицы, называемой протоном.
3.2.Характеристики атомного ядра
1)Зарядовое число. Оно равно числу протонов в ядре, и определяет его заряд, равный Ze . Зарядовое число равно порядковому номеру химического элемента в периодической таблице элементов Д.И. Менделеева.
2)Массовое число А. Оно равно общему числу нуклонов (т.е. протонов
инейтронов) в ядре. Число нейтронов в ядре N A Z .
Для обозначения ядер применяется символ ZA X , где Х – химический
символ данного элемента.
Общее название атомных ядер, отличающихся числами A и Z, –
нуклиды. Нуклиды с различными массовыми и одинаковыми зарядовыми числами называются изотопами. Изотопы являются ядрами одного и того же химического элемента. Из-за разного числа нейтронов ядра разных изотопов одного химического элемента обладают разными массами и могут отличаться по физическим свойствам, например по способности к радиоактивному распаду. Из-за одинакового заряда ядра атомов различных
127
изотопов одного химического элемента имеют одинаковое строение электронных оболочек и поэтому обладают одинаковыми химическими свойствами.
Большинство химических элементов имеет несколько стабильных изотопов. Например, у кислорода имеется три стабильных изотопа: 168 O,
178 O, 188 O ; у олова – десять. Водород имеет три изотопа: 11H обычный водород, или протий ( Z 1, N 0 ); 21H тяжелый водород, или дейтерий
( Z 1, |
N 1); |
31H тритий ( Z 1, |
N 2 ). Протий и дейтерий стабильны, |
тритий радиоактивен.
Ядра с одинаковым массовым числом A называются изобарами ( 4018 Ar и
4020 Ca ).
Наконец, существуют радиоактивные ядра с одинаковыми Z и A, различающиеся периодом полураспада. Они называются изомерами.
Например, существует два изомера ядра 8035 Br ; у одного из них период
полураспада равен 18 мин, у другого – 4.4 ч.
Известно около 1500 ядер, различающихся либо Z, либо A, либо тем и другим. Примерно 1/5 часть всех этих ядер устойчивы, остальные – радиоактивны. Многие ядра были получены искусственным путем с помощью ядерных реакций.
В природе встречаются элементы с атомным номером Z от 1 до 92, исключая технеций (Tc, Z 43) и прометий (Pm, Z 61). Плутоний (Pu, Z 94) после получения его искусственным путем был обнаружен в ничтожных количествах в природном минерале – смоляной обмазке. Остальные трансурановые (т.е. заурановые) элементы (с Z от 93 до 107), были получены искусственным путем посредством различных ядерных реакций.
3.3. Дефект массы и энергия связи ядра
Масса ядра mя всегда меньше суммы масс входящих в него частиц. Это
обусловлено тем, что при объединении протонов и нейтронов в ядро выделяется энергия связи нуклонов друг с другом. Энергия покоя частицы
связана с ее массой соотношением E0 mc2 . Следовательно, энергия по-
коящегося ядра меньше суммарной энергии невзаимодействующих покоящихся нуклонов на величину
Eсв c2 Zmp A Z mn mя .
Эта величина и есть энергия связи нуклонов в ядре. Она равна той работе, которую нужно совершить, чтобы разделить образующие ядро
128

нуклоны и удалить их друг от друга на такие расстояния, при которых они практически не взаимодействуют друг с другом.
В формуле для вычисления энергии связи массу протона mp можно заменить массой атома водорода mH , а массу ядра mя – массой атома mа .
Действительно, если пренебречь сравнительно ничтожной энергией связи электронов с ядрами, указанная замена будет означать добавление к уменьшаемому и вычитаемому выражению, стоящему в фигурных скобках, одинаковой величины, равной Zme . Тогда
Eсв c2 ZmH A Z mn ma .
Этой формулой пользоваться удобнее, так как в таблицах обычно даются не массы ядер, а массы атомов.
Энергия связи, приходящаяся на один нуклон, т.е. Eсв A называется
удельной энергией связи нуклонов в ядре.
Величина
m Zmp A Z ma m я
называется дефектом массы ядра. Дефект массы связан с энергией связи соотношением
m Eсв c2 .
Вычислим энергию связи нуклонов в ядре 42 He, в состав которого входят 2 протона ( Z 2 ) и 2 нейтрона ( N 2 ).
Масса атома 42 He равна 4,00260 а.е.м., чему соответствует 3728,0 МэВ. Масса атома водорода 11H равна 1,000815 а.е.м. (938,7 МэВ). Масса ней-
трона равна 939,57 МэВ. Тогда Eсв 2 938,7 2 939,5 3728 24,8 МэВ.
В расчете на 1 нуклон энергия связи ядра гелия составляет 7,1 МэВ. Для сравнения укажем, что энергия связи валентных электронов в атомах имеет величину, в 106 раз меньшую (порядка 10 эВ). Для других ядер удельная энергия связи, т.е. энергия связи, приходящаяся на 1 нуклон
Eсв A , имеет примерно такую же величину, как у гелия.
На рис. 3.1 изображен график, показывающий зависимость удельной энергии связи Eсв A от массового числа A. Из рисунка видно, что сильнее
всего связаны нуклоны в ядрах с массовыми числами порядка 50-60 (т.е. для элементов от Cr до Zn ). Энергия связи для этих ядер достигает 8,7 МэВ/нуклон. С ростом А удельная энергия связи постепенно умень-
129
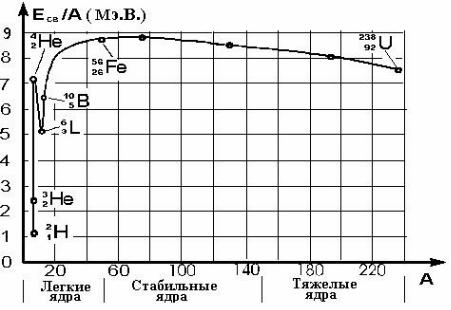
шается; для самого тяжелого природного элемента – урана она составляет 7,5 МэВ/нуклон.
Рис. 3.1
В соответствии с опытом, особо устойчивыми оказываются ядра, у которых число протонов, либо число нейтронов (либо оба этих числа) равно: 2, 8, 20, 28, 50, 82, 126. Эти числа получили название магических.
Ядра, у которых число протонов Z или число нейтронов N является магическим (т.е. особо устойчивые ядра), также называются магическими. Ядра, у которых магическими являются и Z, и N, называются дважды магическими.
Дважды магических ядер известно всего пять:
4 |
16 |
8 ); |
2 He ( Z 2 , N 2 ); |
8 O ( Z 8 , N |
|
2040 Ca ( Z 20 , N 20 ); 2048 Ca ( Z 20 |
, N 28 ); |
|
208 Pb ( Z 82 , N 126).
82
Эти ядра особенно устойчивы. В частности, особенная устойчивость ядра гелия 42 He проявляется в том, что это единственная составная ча-
стица, испускаемая тяжелыми ядрами при радиоактивном распаде (она называется -частицей).
Зависимость удельной энергии связи от массового числа делает энергетически возможным два процесса:
1)деление тяжелых ядер на несколько более легких ядер;
2)слияние (синтез) легких ядер в одно ядро.
Оба процесса должны сопровождаться выделением большого количества энергии. Так, например, деление одного ядра с массовым числом
130
