
1408
.pdf37. С какой минимальной скоростью должны сближаться атом водо-
рода H и ион атома He , чтобы квант света, рождаемый He при переходе n3 3 n2 2 , мог возбудить атом водорода?
Ответ: 0,29c ( с – скорость света).
Контрольные вопросы
1.Опишите ядерную (планетарную) модель атома.
2.В чем заключалось противоречие ядерной модели строения атома с законами классической физики?
3.Сформулируйте квантовые постулаты Бора.
4.Какие состояния атома называются стационарными?
5.Какое состояние называется основным и какие – возбужденными?
6.Как квантуются радиусы стационарных орбит в атоме водорода?
7.Как квантуется энергия электрона в атоме водорода? Чему равна энергия электрона в основном состоянии атома?
8.Как объясняется происхождение линейчатых спектров теорией
Бора?
9.Запишите обобщенную формулу Бальмера.
10.Поясните происхождение спектральных линий в линейчатом спектре водорода с помощью представлений о переходах электронов с одной орбиты на другую и с помощью энергетической диаграммы.
11.Что является источником линейчатых спектров испускания?
12.Что является источником полосатых спектров испускания?
13.В каком случае наблюдается спектр поглощения газа?
2.5.Корпускулярно-волновой дуализм микрообъектов
В1924 г. французский физик Луи де Бройль (1892–1987 гг.) выдвинул гипотезу о том, что корпускулярно-волновой дуализм является универсальным свойством любых материальных объектов, а не только света.
Фотон – не единственная элементарная частица в микромире. Любая микрочастица может проявлять себя одновременно и как частица (с импульсом р и энергией Е), и как волна (с частотой и длиной волны ). Причём формулы, связывающие корпускулярные и волновые характеристики частицы, те же, что и для фотона:
E h hc |
; |
p h |
|
h |
. |
|
|||||
|
|
c |
|
|
|
Поэтому длина волны де Бройля, которая соответствует движущейся микрочастице, обладающейимпульсомр, можетбытьопределенапоформуле
Б |
h |
. |
(2.4) |
|
|||
|
p |
|
|
91
Первое подтверждение гипотезы де Бройля было получено в 1927 г. в опытах по дифракции пучка электронов на монокристалле никеля, выполненных американскими физиками Клинтоном Дэвиссоном (1881–1958 гг.) и Лестером Джермером (1896–1971 гг.), а также независимо от них английским физиком Джозефом Томсоном (1892–1975 гг.), который направлял электроны на золотую фольгу. Картина дифракции электронов на кристаллической решётке оказалась сходной с известной дифракционной картиной рентгеновского излучения с длиной волны, равной значению, определяемому соотношением де Бройля (2.4).
Волновые свойства частиц не являются их коллективной характеристикой, а присущи каждой частице в отдельности. Это подтвердили классические опыты по дифракции поочерёдно летящих электронов, выполненные в 1949 г. российскими физиками В.Ф. Фабрикантом (1907–1992 гг.), Л.М. Биберманом (1907–1992 гг.) и Н.Б. Сушкиным.
Дифракция одиночных электронов оказалась абсолютно идентичной дифракции одиночных фотонов с длиной волны Б . Также, как и для
фотона, можно говорить лишь о вероятности попадания электрона в окрестность определённой точки. Дифракционная картина возникает потому, что вероятность попадания электрона в разные точки экрана неодинакова.
Первоначально волны де Бройля воспринимали как реальный волновой процесс, как своеобразные «волны материи», аналогичные электромагнитным волнам. В ходе дальнейшего развития квантовой теории выявилась некорректность таких представлений, а волны де Бройля получили вероятностную трактовку. На смену «волнам материи» пришли «волны вероятности».
Вероятностный подход к описанию процессов с участием микрообъектов был предопределён исходной квантовой гипотезой, в которой испускание излучения рассматривается как дискретный процесс.
Идея квантования физических величин, гипотеза корпускулярноволнового дуализма и экспериментальные факты, получившие объяснение с помощью зародившихся квантовых представлений, были положены в основу построения одной из наиболее совершенных теорий современного естествознания – квантовой механики.
Квантовая механика – это теория, устанавливающая способ описания и законы движения микрочастиц (элементарных частиц, атомных ядер, атомов, молекул) и их систем (например, кристаллов), а также связь величин, характеризующих частицы и системы, с физическими величинами, непосредственно измеряемыми в макроскопических опытах.
Квантовая механика лежит в основе КПКМ и является базой для развития современного естествознания.
92
2.6. Соотношение неопределённостей
Двойственная природа микрочастиц поставила науку перед вопросом о границах применимости понятий классической физики в микромире.
В классической механике всякая частица движется по определенной траектории и в любой момент времени имеет вполне определенные (точные) значения координаты, импульса, энергии. По-другому обстоит дело с микрочастицей.
Волна этим свойством не обладает. Она не имеет координат. Нет смысла говорить о длине волны в данной точке пространства.
Тогда из корпускулярно-волнового дуализма микрочастиц вытекает совершенно неожиданное правило: если мы точно знаем координаты микрочастицы, то мы совсем не знаем её скорости, и, наоборот, если частица имеет точно определённую скорость, мы ничего не можем сказать о её координатах – принцип неопределённости, установленный немецким учёным Вернером Гейзенбергом (1901–1976 гг.)
Приведём простейшее рассуждение, приводящее к формулировке этого принципа (такие рассуждения называют мысленным экспериментом, провести его с помощью приборов невозможно).
Пусть мы хотим определить координату и скорость электрона. Для этого мы должны его осветить (свет в качестве измерительного устройства!) и зафиксировать координату x . Очевидно, что мы можем измерить координату электрона с точностью до длины волны света (точно также с помощью линейки можно измерить длину стола с точностью до минимального деления её шкалы – 1 мм). То есть точность определения координаты электрона x . Для уточнения положения электрона надо использовать свет с возможно меньшей длиной волны.
Чтобы электрон был виден, с ним должен столкнуться хотя бы один световой квант, имеющий энергию h hc . При взаимодействии с
электроном квант передаёт ему часть своей энергии, которая растёт при уменьшении длины волны света. Это приводит к изменению скорости и импульса электрона. Таким образом, при точном измерении координаты электрона ( x 0 ), его импульс оказывается совершенно неопределённым
( px ).
Для точного определения импульса электрона ( px 0 ) необходимо
использовать свет с большой длиной волны. Однако при этом координата электрона оказывается совершенно неопределённой ( x ).
Пусть x, y, z – неопределённости (абсолютные погрешности) координат движущейся частицы;
93
px , py , pz – неопределённости проекций импульса частицы на
соответствующие оси координат.
Неопределённость координаты частицы и неопределённость проекции импульса частицы на соответствующую ось координат связаны следующими соотношениями, установленными Гейзенбергом в 1927 году:
x px , y py , z pz , (2.5)
где – приведённая постоянная Планка.
Неравенства (2.5) называются соотношениями неопределённостей
Гейзенберга.
Из (2.5) следует, что если микрочастица находится в состоянии с определённым значением координаты, то в этом состоянии соответствующая проекция её импульса оказывается менее определённой. Эта неопределённость принципиальная, её невозможно устранить никаким усовершенствованием измерительного устройства. Она является результатом неконтролируемого воздействия макроскопического измерительного объекта на изучаемый микрообъект. Таким образом, соотношение неопределённостей ограничивает экспериментально достижимую точность измерения характеристик квантовых объектов.
Соотношение неопределённостей справедливо и для других величин, произведение которых имеет размерность постоянной Планка. В частности, неопределённость полной энергии E микрочастицы в некотором квантовом состоянии и неопределенность времени t её пребывания в этом состоянии связаны условием
E t .
Соотношение неопределённостей является предпосылкой недетерминистского, статистического описания микрообъектов. Оно приводит к пониманию того, что поведение микрочастиц носит вероятностный характер и взамен классического понятия траектории для микрочастицы следует использовать понятие распределения вероятности обнаружения частицы в различных точках пространства. Это относится и к движению электрона в атоме, которое не может быть описано совокупностью четко определённых орбит. Более верным является представление об «электронном облаке», частота посещения электроном каждой точки которого задаётся некоторой вероятностью, исчисляемой методами квантовой механики.
94

Примеры решения задач
Пример 1. Найти длину волны де Бройля для электрона, движущегося по первой боровской орбите в атоме водорода.
|
Дано: |
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
||||
e 1,6 10 19 Кл |
|
|
Согласно теории де Бройля движущейся частице |
|||||||||||||||||
m 9,1 10 31 кг |
|
соответствует длина волны |
|
|||||||||||||||||
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
, |
(1) |
|
0 8,85 10 12 Ф/м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
||||||
h 6,62 10 34 Дж·с |
|
где p импульс частицы, |
|
|
|
|
|
|||||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p mc . |
(2) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зависимость |
скорости электрона от порядкового номера орбиты |
||||||||||||||||||
выражается формулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
e2 |
|
|
. |
|
|
|
|
|
(3) |
|||
|
|
|
|
|
|
|
2n 0h |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Подставив (2) и (3) в выражение (1), получим |
|
||||||||||||||||||
|
|
|
|
|
|
h 2n |
h |
|
|
|
2n |
h2 |
|
|||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
. |
|
|
|
||
|
|
|
|
|
m e2 |
|
|
m e2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 8,85 10 12 6,622 |
10 68 |
|
|
e |
|
|
|
|
|
e |
|
|
|
|
|
|
|||
|
3,3 10 |
10 |
|
м. |
|
|
|
|
|
|
||||||||||
9,1 10 31 1,62 |
10 38 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 3,3 10 10 м. |
|
Пример 2. Какой |
кинетической |
|
энергией должен |
обладать протон, |
|||||||||||||||
чтобы длина волны де Бройля протона равнялась его комптоновской длине
волны? |
|
|
|
|
|
|
|
|
|
Дано: |
|
|
|
|
|
Решение |
|
||
Б С |
Длина волны |
де Бройля Б и комптоновская |
C |
||||||
Eк ? |
длина волны определяются по формулам |
|
|||||||
|
Б |
h |
, C |
|
h |
. |
|
||
|
p |
|
|
|
|||||
|
|
|
|
mc |
|
||||
Импульс движущегося протона |
m |
|
|
|
|
||||
|
p |
|
|
. |
|
|
|||
|
|
1 |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
95
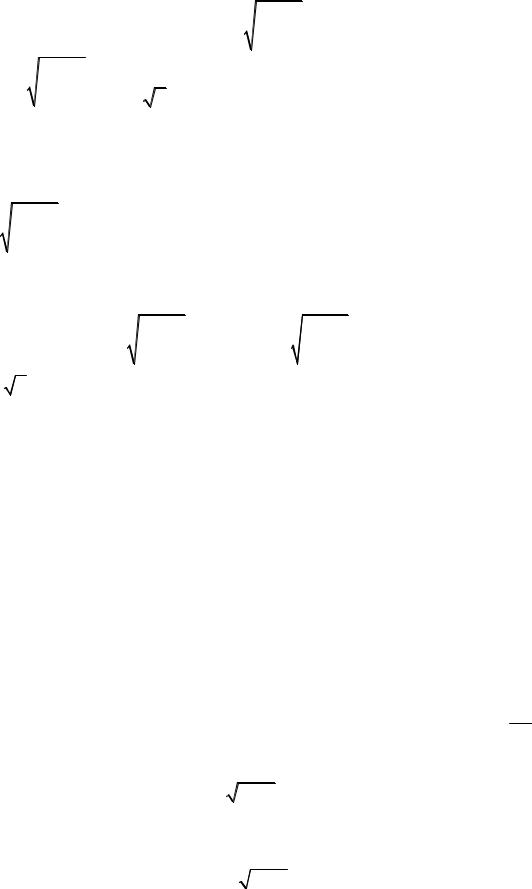
Так как Б С , то |
p mc и mc |
m |
|
|
, |
|
|
|
|||||||||||||
|
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 c2 |
|
|
|
|
|
||
откуда |
|
1 |
2 |
, а |
|
c |
|
. |
|
|
|
|
|
|
|
|
|
|
|
||
c |
c2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Кинетическая энергия протона |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
Eк E E0 , |
EК E E0 , |
|
|
||||||||||||
где E |
|
|
mc2 |
– полная энергия; |
E m c2 |
энергия покоя. |
|||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mc2 |
|
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
E |
|
m c2 |
E |
|
|
|
|
1 . |
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
||||||
|
|
|
|
|
к |
1 |
|
|
|
0 |
0 |
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Eк E0 |
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
c2 |
|
|||||
2 1 1,67 10 27 9 1016 |
0,41 6,23 10 11 Дж. |
||||||||||||||||||||
Ответ: Eк 6,23 10 11 Дж.
Пример 3. Кинетическая энергия электрона в атоме водорода порядка 10 эВ. Используя соотношение неопределенностей, оцените минимальные
линейные размеры атома. |
|
|
|
Дано: |
|
Соотношение |
|
|
|||
me 9,1 10 31 кг |
|
||
E 10 эВ 1,6 10 18 Дж |
|
берга: |
|
r ? |
|
|
px |
где x неопределенность |
|
координаты; |
|
са, приведенная постоянная Планка. |
|
||
Решение неопределенностей Гейзен-
x px ,
– неопределенность импуль-
Предполагая, что x r (линейный размер атома), получим r p .
Импульс электрона, обладающего кинетической энергией E , равен p 2mE.
Предполагая, что по порядку величины p p, оценим r :
r |
|
. |
|
||
|
2mE |
|
96

r |
1,05 10 34 |
0,62 10 10 м. |
|
2 9,1 10 31 1,6 10 18 |
|||
|
|
Ответ: r 0,62 10 10 м.
Пример 4. Используя соотношение неопределенностей Гейзенберга, покажите, что ядра атомов не могут содержать электронов. Считать радиус
ядра равным 10 13 см.
Дано: |
Решение |
|
Rя 10 15 м |
Соотношение неопределенностей Гейзен- |
|
h 6,62 10 34 Дж с |
берга: |
|
|
х рх h 2 , |
|
x –? |
||
|
где x неопределенность координаты; px неопределенность импульса; h постоянная Планка.
Если неопределенность координаты принять равной радиусу ядра, т.е.х Rя , то неопределенность импульса электрона
рх h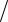 2 x .
2 x .
Так как рх m x , то m x h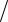 2 x и x h
2 x и x h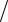 2 x m .
2 x m .
Неопределенность скорости электрона
|
|
6,62 10 34 |
11 |
|
x |
|
|
1,158 10 м/с. |
|
9,1 |
10 31 10 15 6,28 |
|||
|
|
Ответ: x 1,158 1011 м/с.
Пример 5. Атом испустил фотон с длиной волны 0,55 мкм. Продол-
жительность излучения t 10 нс. Определите наименьшую погрешность, с которой может быть измерена длина волны излучения.
Дано: |
|
|
|
|
Решение |
|
|
0,55 мкм 0,55 10 6 м |
|
|
Энергия фотона |
c |
|
||
t 10 нс |
|
|
|
|
E h v h |
, |
|
|
|
|
|
|
|
||
? |
|
|
|
|
|||
dE hc d |
или E hc |
|
, откуда |
E 2 . |
|
|
|
2 |
|
|
2 |
|
hc |
|
|
Соотношение неопределенностей Гейзенберга для энергии и времени
E t 2h .
97
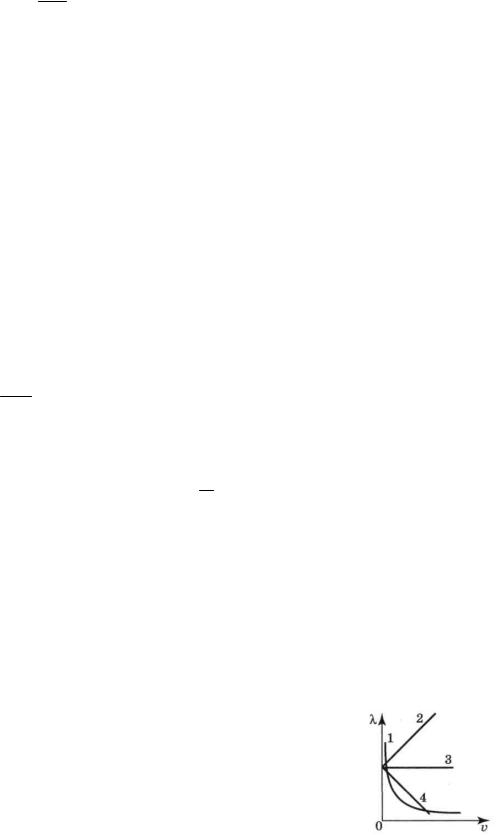
Отсюда E t2h .
Подставляя E в формулу для , |
получим |
2 |
. |
|||||||
t2 c |
||||||||||
|
|
|
|
0,55 10 6 2 |
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
1,6 10 14 |
м. |
|
|
||
10 |
8 |
8 |
|
|
||||||
|
|
2 3,14 3 10 |
|
|
|
|
||||
Ответ: 1,6 10 14 м
Пример 6. Покажите, как условие квантования момента импульса электрона в теории Бора атома водорода можно сформулировать с учетом гипотезы де Бройля о наличии у электрона волновых свойств.
Решение:
Для электрона, движущегося по круговой орбите радиуса r , момент импульса L pr , где p импульс электрона.
Поэтому условие квантования me nrn nh n , можно преобразовать к
2
виду 2 r n 2p .
Согласно гипотезе де Бройля движение электрона следует связать с волновым процессом, длина волны которого
Б hp 2ph .
Поэтому условие квантования Бора можно записать как
2 r n Б , n 1, 2, 3….
Это соотношение утверждает, что стационарными являются только такие орбиты, на длине которых укладывается целое число длин волн де Бройля для движущегося по орбите электрона.
Задачи для самостоятельного решения
Средний уровень
1.На каком из графиков (см. рисунок) правильно показана зависимость длины волны де Бройля электрона от его скорости?
2.Как изменилась длина волны де Бройля при возрастании и массы, и скорости нерелятивистской частицы в 2 раза?
98

3. Два электрона движутся со скоростями и 2 . Сравните длины волн де Бройля 1 и 2 , соответствующие первому и второму электрону.
1) 1 > 2 ; |
2) 1 < 2 ; |
|
3) 1 2 . |
|
4. Укажите частицу, обладающую наименьшей длиной волны, если |
||||
скорости частиц одинаковы. |
|
|
||
1) |
альфа-частица; |
|
2) |
электрон; |
3) |
нейтрон; |
|
4) |
протон. |
5.Чему равно отношение длин волн де Бройля протона и нейтрона, если они двигаются с одинаковыми скоростями?
Ответ: 1.
6.Найдите отношение скоростей протона и альфа-частицы, длины волн де Бройля которых одинаковы.
Ответ: 4.
7. Отношение скоростей двух микрочастиц |
1 |
4. Чему равно отно- |
|||
2 |
|||||
|
m1 |
|
|
||
шение масс этих частиц |
, если их длины волн де Бройля удовлетворяют |
||||
m |
|||||
соотношению Le ? 2 Ответ: 1/ 2 .
8. Электрон падает нормально на щель шириной a со скоростью y . Укажите верные утверждения:
1)с уменьшением a неопределенность импульса px возрастает;
2)определить точно координату и импульс электрона, пролетающего сквозь щель, невозможно;
3)с ростом угла дифракции неопределенность импульса электрона
уменьшается; 4) длина волны де Бройля электрона, пролетающего сквозь щель,
mh .
9.Укажите верные утверждения:
1)чем точнее определена скорость микрочастицы, тем больше неопределенность ее координаты;
2)гипотезу де Бройля впервые на опыте подтвердили Дэвиссон и Джермер;
99

3) в опыте Дэвиссона и Джермера длина волны де Бройля электрона
рассчитывалась по формуле |
h |
, где U – ускоряющее напряжение; |
|
2eUm |
|||
|
|
4) если одиночный электрон падает нормально на щель шириной a со скоростью y , то неопределенность его импульса px a .
10. Электрон летит сквозь щель шириной a со скоростью y . Укажите
верные утверждения.
1) неопределенность его координаты x a ;
2) py h h ;
a
3) px py tg , где – угол дифракции;
4) чем меньше ширина щели, тем меньше неопределенность импульса электрона.
11. Укажите верные утверждения:
1) формула де Бройля справедлива для фотона;
2) x px меньше ;
3) все движущиеся микрочастицы обладают волновыми свойствами;
4) движущиеся молекулы обладают волновыми свойствами.
12. Электронлокализованвпространствевпределах x 1,0 мкм. Учитывая, что постоянная Планка 1,05 10 34 Дж с, а масса электрона m 9,1 10 31 кг, найдитенаименьшеезначениенеопределенностискорости x .
Ответ: x 117 м/с.
13. Высокая монохроматичность лазерного излучения обусловлена относительно большим временем жизни электронов в метастабильном
состоянии – 10 3 с. Учитывая, что постоянная Планка 6,6 10 16 эВ с, найдите ширину метастабильного уровня.
Ответ: E 6,6 10 13 эВ.
Достаточный уровень
1. Нейтрон с кинетической энергией E 25эВ налетает на покоящийся
дейтон (ядро тяжелого водорода). Найдите дебройлевские длины волн обеих частиц в системе их центра инерции.
Ответ: для обеих частиц 8,6пм.
100
