1385

временных сдвигов двух соседских узлов так, чтобы не превышалась пропускная способность перегона между ними.

Как видим, основной задачей управления насыщенными транспортными потоками является балансировка транспортного спроса и предложения на заранее определенных транспортным инженером связях (перегонах городских улиц). Балансировка достигается путем модификации весовых коэффициентов целевой функции управления или определяющих соотношений, причем значение корректирующих коэффициентов устанавливается транспортным инженером на основе собственного опыта.

31

2. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ УПРАВЛЕНИЯ НАСЫЩЕННЫМИ ТРАНСПОРТНЫМИ ПОТОКАМИ

2.1. Математическая модель задержки и длины очереди на изолированном перекрестке

Продолжительность задержки транспортных средств получила широкое применение в качестве критерия оптимизации управления, как на отдельном пересечении, так и сети. Существует два основных подхода к определению задержки транспортных средств. Первый подход основан на макроскопической модели описания транспортного потока и определяет задержку как потери времени на вынужденные остановки транспортных средств перед перекрестками, железнодорожными переездами, при заторах на перегонах, а также из-за снижения скорости транспортного потока по сравнению со средней скоростью свободного движения на данном участке дороги:

где vifree – скорость свободного движения на i-м участке; vi – наблюдаемая скорость движения на i-го участке; li – длина i-го участка.

Второй подход определяет задержку в терминах системы массового обслуживания как среднее время ожидания автомобиля в очереди. Под длиной очереди при этом понимается количество транспортных средств, ожидающих обслуживания перед перекрестком.

На практике первый подход, как правило, используется для оценки качества проектных решений по организации движения, в то время как второй подход к определению задержки получил распространение при решении задач оптимального управления светофорными объектами.

По характеру описания свойств транспортного потока принято различать детерминированные и стохастические модели задержки. В практике управления дорожным движением получили распространение модели, сочетающие в себе как детерминированную, так и стохастическую составляющие задержки.

Детерминированная составляющая задержки определяется в условиях стационарности движения:

–в начале разрешающего сигнала очередь равна нулю;

–транспортные средства прибывают одинаковыми группами с интенсивностью движения q за цикл;

32

–разъезд осуществляется одинаковыми группами с интенсивностью равной потоку насыщения S при наличии очереди, и с интенсивностью равной интенсивности прибытия при ее разъезде;

–спрос транспортных средств не превышает пропускной способности элемента перекрестка, которую определяют как отношение потока насыщения S к отношению разрешающего сигнала ко времени цикла (g/c).

Упрощенно процесс формирование очереди транспортных средств можно представить в форме диаграммы (рис.2.1).

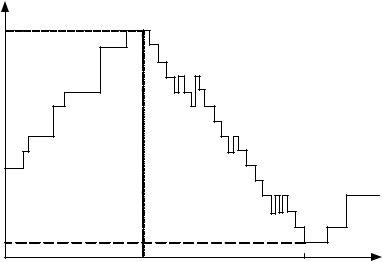
На запрещающий сигнал rформируется очередь транспортных средств с интенсивностью q(t). При включении разрешающего сигнала g начинается разъезд очереди с интенсивностью q-S, при этом количество транспортных средств в очереди принимает максимальное значение Qmax. Область под линией профиля очереди (рис. 2.2) представляет собой детерминированную задержку за цикл.

Впервые модель оценки задержки при жестком светофорном регулировании была предложена Beckmann М. [20] с допущением о биноми-

33

нальном процессе прибытия транспортных средств и детерминированном характере процесса обслуживания:

где с – длительность цикла; g – эффективная длительность зеленого сигнала; q – интенсивность прибытия транспортных средств; S – интенсивность разъезда из очереди; Q0 – величина остаточной очереди.

Q(t)

Q(t)

Q(0)

Q(c)

Рис. 2.2. Процесс образования очереди в течение одного цикла (по исследованиям D.McNeil 1986)

Позднее Little в [68]исследовал величину задержки на регулируемом

пересечении при пуассоновском распределении транспортного потока, Darroch J.N. [30] процесс прибытия представлял обобщенным пуассоновским процессом:

сивность прибытия; h – длина интервала во времени; А – число прибытий в течение интервала A q h .

McNeil D.R. [74] исследовал величину задержки в предположении об общности процесса прибытия транспортных средств и постоянстве вре-

34

мени разъезда. Общая задержка за цикл представлялась как сумма двух составляющих:

где W1 – общая задержка в фазе красного сигнала; W2 – общая задержка в фазе зеленого сигнала.

c-g

где Q(t) – длина очереди в момент времени t; A(t) – кумулятивное число прибытий в момент времени t.

В работе [56] Herman R. и Weiss G. рассматривая случай сложного пуассоновского процесса прибытия и общего процесса обслуживания получили следующую модель:

Исследование уравнения показало, что в случае отсутствия начальной задержки (Q0 0 ) и случайности транспортного процесса (I=0), получен-

ная задержка является постоянной составляющей задержки. Этот компонент может быть получен из простой модели с постоянным прибытием за цикл и процессом обслуживания, описанным выше. В более общем случае уравнение (2.7) требует дополнительных данных о размере очереди и величине остаточной очереди – основных ограничениях использования полученной формулы на практике.

Необходимость учета остаточной очереди послужила стимулом в проведении исследований по получению закрытой формы уравнения остаточной очереди [48, 86, 87, 30], однако оно так и не было получено.

Необходимость оценки остаточной очереди и наличие строгих ограничений, накладываемых предположением о законе распределения прибытия транспортных средств, ограничивает применимость «точных» моделей на практике. Это положило начало исследованиям по получению приближенных формул (моделей с элементами аппроксимации) для оценки задержек с более простыми и ограничениями, которые способны учитывать разнообразие реальных условий.

35

Первая, широко известная приближенная формула, была получена Webster F.V. [109, 110] при сочетании теоретического подхода и численного моделирования:

где d – средняя задержка за цикл, с; с -длина цикла регулирования, с; g – эффективная длительность зеленого сигнала, с; х – степень насыщения (отношение интенсивности движения к пропускной способности); q – интенсивность прибытия, авт/ч.

Первая составляющая уравнения (2.8) представляет задержку, при условии стационарности прибытия транспортного потока, а вторая составляющая определяет случайную составляющую процесса. Последняя известна как «случайная задержка», в предположении о пуассоновском процессе прибытия и постоянной интенсивности разъезда транспортных средств, которая соответствует пропускной способности. Третья составляющая представляет собой корректирующее слагаемое.

Дальнейшая аппроксимация уравнения (2.7) была направлена на упрощение за счет сокращения третьего и четвертого члена уравнения, которые, как правило, имеют намного меньший порядок, чем первые два. Этот подход использован в работе Miller A.J. [79] при выводе аппроксимирующей формулы:

Формула получена путем исключения второго и третьего члена уравнения (2.7). Miller также получил выражение для насыщенной очереди при пуассоновском прибытии и времени обслуживания равному продолжительности разрешающего сигнала:

В последствие Newell модифицировал формулу (2.9) путем добавления дополнительного корректирующего члена, позволившего повысить точность определения задержки при средней загрузке:

Дальнейшие попытки повышения точности моделей не привели к существенным результатам.

36

Второй подход предусматривает моделирование транспортного потока на перекрестке, предполагая стабильность процессов прибытия и обслуживания но, не предполагая обязательного достижения стохастического равновесия. При этом проводится оценка средней задержки, и длины очереди для рассматриваемого периода времени. Данный подход предусматривает аппроксимацию интенсивности прибытия некоторой функцией времени (ступенчатая, параболическая или треугольная функция) и определение соответствующей значения задержек.

В последнее время популярность приобрел метод трансформации координат. Хотя метод и использует стабилизированную кривую очереди, полученную по классической теории, в результате получается временнозависимая формула задержки.

Основой развития данного метода послужили следующие наблюдения:

–при низкой степени насыщения (х<<1)задержка всегда равна такому значению, которое может быть при постоянной плотности в течение всего времени;

–при высокой степени насыщения (х>>1) задержка может быть описана с разумной степенью точности следующим детерминированным выражением:

где d1 – задержка, наблюдаемая при низкой плотности (постоянная за-

держка); Т – анализируемый период, в течение которого интенсивность движения стабильна;

– модели задержки при стабильных состояниях асимптотически приближаются к оси y(y=q/S), т.е. дает бесконечную задержку при насыщенном состоянии (х=q/С=1). Метод трансформации координат передвигает первоначальную кривую метода стабильных состояний до асимптотического приближения к детерминированной линии перенасыщения (рис. 2.3) – второй составляющей уравнения (2.16).

Горизонтальное расстояние между предложенной кривой задержки и ее асимптотой равно расстоянию между кривой «стабильной» модели и вертикальной линией х=1.

Имеется два ограничения относительно применения формулы:

1)первоначальная длина очереди равна нулю (в начале периода [0,Т]);

2)интенсивность движения постоянна в течение периода [0,Т].

В результате моделирования установлена адекватность полученного метода. Таким образом, такая техника является полезной в практике. Принципиальный недостаток заключается в добавление ограничений, которые недостаточно теоретически обоснованы. Указанные выше трудности были

38

Для выполнения практических расчётов задержки транспортных средств как в условиях не насыщенного движения (v/c<1,0), так и в условиях перенасыщения (v/c> 1,0) хорошо себя зарекомендовала модель

Highway Capacity Manual (HCM) [57, 58]. Модель задержки былаполучена с использованием, как эмпирических данных, так и теоретических соотношений. Уравнение включает три составляющих задержки:

PF – фактор прогрессии; d2 – случайная задержка (incremental delay), с/авт.; d3 – задержка перенасыщения (initial queue delay).

Постоянная составляющая задержки вычисляется как:

где C – длительность цикла, с; g/C – отношение длительности разрешающего сигнала к циклу регулирования для группы полос движения; X – степень насыщенности группы полос движения (v/c); c – пропускная

39

способность группы полос движения c s gC , авт/ч; s – поток насыще-

ния для группы полос движения, авт/ч; v – транспортный спрос. Случайная задержка определяется с учетом не стационарности про-

цесса формирования очереди:

где T – продолжительность периода анализа в часах; k –коэффициент корректировки, учитывающий способ управления (адаптивное или предрассчитанное); I – коэффициент корректировки, учитывающий влияние соседних перекрестков.

Для предрассчитанного управления величина k = 0,50. Для тран- спортно-зависимых контроллеров величина k вычисляется как функция степени насыщенности и kmin, используя следующую формулу:

где X – величина, меньшая 0,5 устанавливается равной 0,5; kmin – времен-

ной интервал, характеризующий наличие разрыва в транспортном потоке. Результирующее влияние величины k должно уменьшить задержку при транспортно-зависимом управлении, в условиях низких степеней насы-

щенности.

Величина I-фактора равна 1,0 для изолированных регулируемых пересечений. Для координированных пересечений, величина I-фактора является функцией от степени насыщенности расположенных по ходу движения направлений (Xu):

Когда степень насыщенности восходящего потока больше чем 1,0, устанавливается равным 1,0, что в свою очередь ограничивает I-фактор минимальной величиной 0,09. Результирующее влияние I-фактора должно уменьшить задержку потоков, которые насыщены по ходу движения. Другими словами, движение в ненасыщенных условиях, имеет более широкое разнообразие профилей транспортного потока, таким образом, увеличивая вероятности неэффективного использования фазы на расположенном вниз по ходу движения пересечении.

Задержка перенасыщения определяется величиной остаточной очереди на анализируемом периоде по формуле