Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1321

.pdf

Скачиваний:

Добавлен:

16.06.2024

Размер:

1.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

Разложим внешнюю нагрузку в такой же двойной тригонометрический ряд:

	m x		n y
q x, y Cmn sin		sin		.	(53)
	a
m 1 n 1			b

Коэффициенты этого ряда определяются по формуле, известной из курса высшей математики:

Cmn

a b q x, y sin

m x

sin

n y

dxdy.

0 0

Теперь уравнение (52) можно записать так:

m x

n y

Amn

sin

m 1 n 1

m x

n y

Cmn sin

sin

D m 1 n 1

(54)

(55)

Приравнивая коэффициенты при соответствующих тригонометрических функциях левой и правой части в формуле (55), будем иметь:

Amn m 4 2 m 2 n 2 n 4 sin m x sin n ya a b b a b

CDmn sin ma x sin nby ,

Отсюда получаем:

Amn				Cmn				.	(56)
Amn				2		2	a 2 2	.	(56)
	D 4			2		2	a 2 2
			m		n
	a	4	m		n
	a						b

Для равномерно распределенной нагрузки q, приложенной по площади

прямоугольника а1 x а2, b1 y b2 формулу (54) можно представить в виде:

Cmn

4q a2 sin

m x

dxb2 sin

n y

dy.

Произведя интегрирование, получим:

Cmn

m a

n b

cos

ab m n

или, после элементарных преобразований

Cmn

m a

n b

cos

(57)

Подставляя (57) в (56) получим окончательное выражение для коэффициентов Amn :

A qa4

mn D

m a

cos

a 2

mn m

(58)

	n b		n b
cos	2	cos	1	.
cos	b	cos	b	.
	b		b

Таким образом, расчёт пластины сводится к определению коэффициентов Cmn по формулам (54) от конкретно заданной нагрузки, после чего по

формулам (56) определяются значения коэффициентов ряда Amn , а по вы-

ражению (51) – значения прогибов пластины.

Далее, на основании формул (38) приведём выражения для изгибающих моментов

m x

n y

M x D

D Amn

sin

;

m 1 n 1

m x

n y

M y D

D Amn

sin

;

m 1 n 1

крутящего момента

m x

n y

M xy D 1

D 1 Amn 2

cos

;

x y

m 1 n 1

и поперечных сил:

mn2

m x

n y

Qx D

D Amn

2 cos

sin

;

x y

m 1 n 1

nm2

m x

n y

Qy D

D Amn

sin

cos

m 1 n 1

(59)

(60)

(61)

Выражения для приведённых поперечных сил (опорных реакций) имеют следующий вид:

V Q

M xy

3w 2

x x

x y2

mn2

m x

n y

D Amn

3 2

cos

sin

;

m 1 n 1

(62)

M xy

Vy Qy

x2 y

nm2

m x

n y

D Amn

3 2

sin

cos

m 1 n 1

Приведём ещё формулы для сосредоточенных реакций в углах пластины, положительные направления которых показаны на рис. 16. На рис. 16 показаны также положительные направления равнодействующих приведённых поперечных сил Rx0 , Ry0 , Rxa , Ryb . Поскольку

R 2M xy

то получаем:

1)угол при x

	2 m	n				m x			n y
2D 1 Amn			cos			m x		cos	n y	,
2D 1 Amn			cos					cos	b	,
m 1 n 1	a	b					a		b
0, y 0
				m	n
R1 2D 1 Amn 2				m	n		;
m 1 n 1				a		b

2)	угол при x a,	y 0
							n
	R2 2D 1 Amn 2 m						n	cosm ;
			m 1 n 1			a	b
3)	угол при x a,	y b
				m	n
	R3 2D 1 Amn 2			m	n	cos m cos n ;
		m 1 n 1		a	b
4)	угол при x a,	y 0

(63)

(64)

(65)

	m	n
R4 2D 1 Amn 2	m	n	cosn ;	(66)
m 1 n 1	a	b

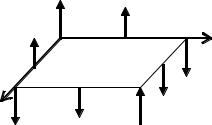
Из сопоставления соотношений (59)-(66) следует, что если прогиб пластины w x, y зависит от её цилиндрической жёсткости D , то внутренние

R		Ry0
1		X
Rx0		X
		a
b		R2
Y		Rxa
R4	Ryb	R3

усилия и опорные реакции от цилиндрической жёсткости D не зависят, поскольку коэффициенты Amn множитель

D содержит в знаменателе.

Рис. 16

Задание

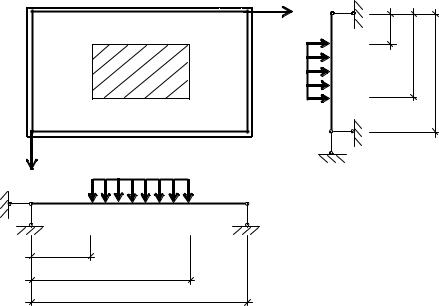
Требуется подобрать толщину прямоугольной пластины, изображённой на рис. 17, из условия прочности по теории Треска – Сен-Венана и по теории прочности Губера – Мизеса – Генки. Результаты сравнить.

Прямоугольная пластина, шарнирно опёртая по всему контуру, загружена равномерно распределенной нагрузкой интенсивностью q по площа-

ди прямоугольника ABCD, испытывает поперечный изгиб.

Для определения внутренних усилий в пластине следует использовать метод двойных тригонометрических рядов Фурье (метод Навье). Приближённое уравнение изогнутой срединной поверхности пластины (51) представить в виде четырёх членов ряда:

w x, y A	sin x	sin y		A	sin x sin 2 y
11	a		b	12		a	b	(а)

A sin 2 x sin y			A sin 2 x			sin 2 y .

21	a	b		22	a		b

Порядок решения задачи
1. Вычисляем коэффициенты A11,			A12 ,	A21,	A22	по формулам (58).

2.Получаем приближённое уравнение изогнутой поверхности срединного слоя.

3.Определяем внутренние усилия: изгибающие моменты по соотношениям (59, крутящий момент – по соотношениям (60), поперечные силы – по соотношениям (61).

4.Строим эпюры прогибов и изгибающих моментов. Для сечения

x, y , M x x, y ; для сечения ym 0,5b – эпюры

x, y , M y x, y .

5.Подбираем толщину пластины.

6.Определяем распределённые опорные реакции по соотношениям (62)

истроим их эпюры.

7. Определяем сосредоточенные опорные реакции в углах пластины по формулам (63)-(66).

		X
A	D	q
Y	q

Рис. 17

Пример решения конкретной задачи.

Дано: a 3 м, b 1 м, a1 0,5	м, a2 2,5 м, b1 0,25 м,	b2 0,75 м,
q 8 105 МПа, 0,2 ,	R 2,1 108 МПа .

Решение

1. Вычисляем коэффициенты A11, A12 , A21, A22 . В соответствии с формулами (58), получаем:

A	8 105		34			4							1						cos1 2,5 cos1 0,5
A	8 105																2		cos1 2,5 cos1 0,5
11	D							6								2	2				3				3
	D											2	2		3	2					3				3
										1 1 1			1
															1

			1 0,75								cos	1 0,25						6,604			103		Нм	2	;
	cos			1							cos		1							D			Нм		;
				1									1							D
A	8 105		34		4								1							cos	1 2,5 cos1 0,5
A	8 105																	2		cos	1 2,5 cos1 0,5
12	D						6								3 2			2			3				3
	D											2	2	2	3 2						3				3
									1 2 1				2
															1

		2 0,75									cos	2 0,25						0,00			Нм	2	;
	cos			1							cos		1							D	Нм		;
				1									1							D

A	8 105 34				4							1								cos 2 2,5 cos 2 0,5
A	8 105 34						6										2			cos 2 2,5 cos 2 0,5
21	D						6							3 2			2						3				3
	D									2	2	2		3 2									3				3
									2 1	2		1
														1

			1 0,75						cos	1 0,25						0,00						Нм	2		;
	cos			1					cos			1						D				Нм			;
				1								1						D
A	8 105		34		4							1									cos 2 2,5 cos						2 0,5
A	8 105					6												2			cos 2 2,5 cos
22	D					6									3 2			2						3			3
	D									2	2	2	2		3 2									3			3
								2 2		2		2			1
															1

		2 0,75							cos	2 0,25						0,00						Нм		2		.
	cos			1					cos			1							D			Нм				.
				1								1							D

2. Составляем приближённое уравнение изогнутой поверхности сре-

динного слоя. Подставляя значения приведённых коэффициентов Amn в выражение (а), будем иметь:

w x, y	6,604 103	sin	x	sin	y .	(б)
	D		3		1

3. Определяем внутренние усилия. На основании соотношений (59)– (61), находим:

M x 6,604 10		3			2			12		0,2			12			sin		x			sin		y		;
M x 6,604 10									2	0,2			2			sin			3		sin			1	;
							3		2				2
							3						1
M y 6,604 103 2								2		0,2			2			sin x sin y ;
M y 6,604 103 2								1		0,2			1			sin x sin y ;
								2					2							3				1
							1						3							3				1
M xy 1 0.2			6,604 103 2												1		cos				x	cos			y	;	(в)
M xy 1 0.2			6,604 103 2												3	1	cos				3	cos			1	;	(в)
															3	1					3				1
Qx 6,604 10	3			3		13					12						x					y
														cos						sin				;
								3			2			cos			3			sin		1		;
								3			2
						3						3 1
Qy 6,604 10	3			3		13					12			sin			x			cos		y
																								.
								3			2						3					1		.
						1					1 3						3					1

4. Строим эпюры прогибов и изгибающих моментов по точкам в се-

чении xm 0,5a и в сечении ym 0,5b . На основании соотношений (в), по-

лучим:

- сечение xm 0,5a :

w 1,5; y	6,604 103							sin			sin y .
			D						2					1
	3			2			12	0,2		12				sin		sin		y		;
M x 1,5; y 6,604 10							2	0,2			2			sin	2	sin		1		;
						3				1					2			1
- сечение ym 0,5b :
w x;0,5	6,604 103							sin	x				sin .
			D							3				2
M y x;0,5 6,604 10		3			2		12	0,2		12				sin	x		sin			.
M y x;0,5 6,604 10							2	0,2				2		sin	3		sin		2	.
							2					2
						1				3

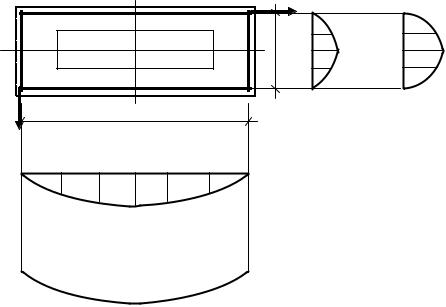
Соответствующие графики представлены на рис. 18.

			X
			4,67	1,43
		b	6,60	2,03
		b	4,67
			4,67	1,43
а			wD 10 3	M x 10 4
Y
5,72	5,72	wD 10 3
		wD 10 3

3,30	6,60	3,30
5,77	5,77		M y 10 4
			M y 10 4

3,33		3,33
3,33	6,66	3,33
	6,66

Рис. 18

Вычисления прогибов и изгибающих моментов сведены в табл. 12. Таблица 12

	Сечение xm=0,5a			Сечение ym=0,5b
y, м	Прогиб, Нм м	Момент Mx, Н	x, м	Прогиб, Нм м	Момент My, Н

0	0,00E+00	0,00E+00	0	0,00E+00	0,00E+00
0,25	4,67E+03	1,43E+04	0,5	3,30E+03	3,33E+04
0,5	6,60E+03	2,03E+04	1	5,72E+03	5,77E+04
0,75	4,67E+03	1,43E+04	1,5	6,60E+03	6,66E+04
1	0,00E+00	0,00E+00	2	5,72E+03	5,77E+04
			2,5	3,30E+03	3,33E+04
			3	0,00E+00	0,00E+00

5. Подбираем толщину пластины. Из эпюр изгибающих моментов следует, что самые большие моменты, а, следовательно, в соответствии с формулами (40) и самые большие нормальные напряжения x и y возникают

вцентре пластины x xm , y ym на верхней и нижней её поверхности.

Всилу симметрии крутящий момент в центре пластины M xy 0 и, сле-

довательно, xy 0 . Таким образом, в наиболее опасной точке xm , ym имеем плоское напряжённое состояние z 0, zx 0, zy 0 и напря-

жения x xm , ym , h 2 и y xm , ym , h		2 являются главными нормаль-
ными напряжениями. Поскольку M x 0		и M y 0 , то знак у напряжений
x и y будет определяться знаком координаты z (см. формулы (40)), то
	h
есть на верхней грани пластины z	2	оба напряжения будут положи-

тельными, на нижней		h	– отрицательными. Учитывая значение
	z	2

моментов M x и M y		в точке		xm , ym , получаем: x 2 и y 1 посколь-
ку, как известно, 1 2 3				и для пластин 3		0 .
В соответствии		с теорией прочности				Треска – Сен-Венана			(14)
1 3 R , толщина пластинки будет определяться по формуле
			M y xm , ym		6 R .				(г)
					6 R .				(г)
		1		h2
				h2
Отсюда находим минимальную толщину пластины:
h	6M y xm , ym			6 6,663 104			2
				8	4,363 10			м 4,36 см.	(д)
	R			8	4,363 10			м 4,36 см.	(д)
	R			2,1 10

В соответствии с теорией прочности Губера – Мизеса – Генки (16)

2 R , толщина пластины будет опре-

деляться по формуле

, y

x , y

2 , и будет

равна

h 4,111 10 2

м 4,111 см.

(е)

В качестве расчётной толщины плиты принимаем h 4,111 см.

6.Определяем распределённые реакции. На основании соотношений

(62)получаем

1) 0 x a,		y 0
Vx 6,604 10		3				13			2			0,2	1 12					cos			1 x				sin		1 y	0;
Vx 6,604 10							3		2			0,2			2			cos					3		sin		1	0;
							3								2
				3									3 1
Vy 6,604 10		3			13			2			0,2		1 12					sin		1 x				cos			1 y
Vy 6,604 10						3		2			0,2		1		2			sin					3	cos			1
					1								1		3								3				1
6,604 10			3			13			2 0,2					1 12					sin			1	x		7,925 10				3	sin			x	.
6,604 10							3		2 0,2						2				sin				3		7,925 10					sin			3	.
							3								2
						1								1 3
2) 0 x a,		y b
Vx 6,604 10		3				13			2			0,2	1 12					cos			1 x				sin		1 y	0;
Vx 6,604 10							3		2			0,2			2			cos					3		sin		1	0;
				3									3 1										3				1
Vy 6,604 10		3			13			2			0,2		1		12			sin		1 x				cos			1 y
Vy 6,604 10						3		2			0,2		1		2			sin					3	cos			1
						3									2
					1										3
6,604 10					3		13			2 0,2					1	12							1 x			7,925 10					3	sin		x	.
6,604 10									3	2 0,2					1		2		sin				3			7,925 10						sin		3	.
									3								2
							1									3
3) x 0,	0 y b

	3				13		2 0,2	1	12		cos			1 x				sin		1 y
Vx 6,604 10					3		2 0,2			2	cos					3		sin			1
					3					2
			3					3 1
6,604 10			3		13		2 0,2	1	12		sin		1		y			0,711 10				3	sin y;
6,604 10					3		2 0,2	3		2	sin					1		0,711 10					sin y;
					3					2
			3							1
Vy 6,604 10		3		13			2 0,2	1 12			sin		1		x			cos		1	y	0.
Vy 6,604 10					3		2 0,2			2	sin					3		cos			1	0.
				1				1 3								3					1
4) x a,	0 y b
	3				13		2 0,2	1	12		cos			1 x				sin		1 y
Vx 6,604 10					3		2 0,2			2	cos					3		sin			1
					3					2
			3					3 1
6,604 10				3		13	2 0,2			1 12						1	y		0,711 10					3	sin y;
6,604 10						3	2 0,2				2	sin					1		0,711 10						sin y;
						3					2
					3					3 1
Vy 6,604 10		3		13			2 0,2	1 12			sin		1		x			cos		1	y	0.
Vy 6,604 10					3		2 0,2			2	sin					3		cos			1	0.
					3					2
				1				1 3

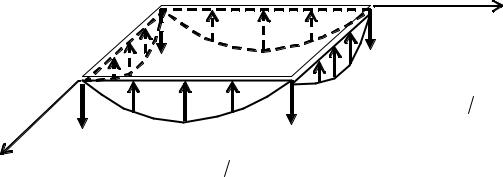
7. Строим эпюры распределённых реакций. В соответствии с полу-

ченными формулами для приведённых поперечных сил Vx и Vy строим

эпюры распределённых реакций по точкам (рис. 19). Вычисления показывают, что распределённые реакции вдоль контура пластины направлены вверх и одинаковы на противоположных сторонах пластины. Результаты вычислений сведены в табл. 13.

R 3,476 104 , Н									X
R 3,476 104 , Н
1							R2		3,476 104 , Н
							R2		3,476 104 , Н
							5,03
							7,11
R4 3,476 104 , Н	5,60				5,60	5,03	Vx 10 2, Н м
R4 3,476 104 , Н	5,60	7,93			5,60	3,476 10		4	, Н
Y		7,93			R3	3,476 10			, Н
Y		Vy 10	3	,	Н м
		Vy 10		,	Н м

Рис. 19

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.06.20241.54 Mб11317.pdf
#
16.06.20241.54 Mб21318.pdf
#
16.06.20241.54 Mб01319.pdf
#
16.06.2024201.45 Кб1132.pdf
#
16.06.20241.54 Mб11320.pdf
#
16.06.20241.54 Mб41321.pdf
#
16.06.20241.54 Mб11322.pdf
#
16.06.20241.55 Mб11323.pdf
#
16.06.20241.55 Mб21324.pdf
#
16.06.20241.55 Mб11325.pdf
#
16.06.20241.56 Mб21326.pdf