
1283
.pdfПродолжение прил. 3
5.Результат расчетов по вышеприведенным формулам и функциям.
5.1.Расчет по дифференциальным функциям:
|
fN(t) = |
|
fNm(t) = |
|
fW(t) = |
|
|
|
fVm(t) = fG(t) = |
||||||||
1,118 10-7 |
|
1,118 10-7 |
|
8,101 10-8 |
|
8,101 10-8 |
|
5,376 10-17 |
|
||||||||
2,458 10-6 |
|
2,458 10-6 |
|
6,118 10-6 |
|
6,118 10-6 |
|
2,501 10-9 |
|
||||||||
3,017 10-5 |
|
3,017 10-5 |
|
5,602 10-5 |
|
5,602 10-5 |
|
3,416 10-6 |
|
||||||||
2,067 10-4 |
|
2,067 10-4 |
|
2,467 10-4 |
|
2,467 10-4 |
|
1,349 10-4 |
|
||||||||
7,901 10-4 |
|
7,901 10-4 |
|
7,164 10-4 |
|
7,164 10-4 |
|
8,735 10-4 |
|
||||||||
1,686 10-3 |
|
1,686 10-3 |
|
1,472 10-3 |
|
1,472 10-3 |
|
1,885 10-3 |
|
||||||||
2,007 10-3 |
|
2,007 10-3 |
|
2,021 10-3 |
|
2,021 10-3 |
|
1,941 10-3 |
|
||||||||
1,334 10-3 |
|
1,334 10-3 |
|
1,575 10-3 |
|
1,575 10-3 |
|
1,174 10-3 |
|
||||||||
4,948 10-4 |
|
4,948 10-4 |
|
5,241 10-4 |
|
5,241 10-4 |
|
4,753 10-4 |
|
||||||||
1,024 10-4 |
|
1,024 10-4 |
|
4,88 10-5 |
|
4,88 10-5 |
|
1,407 10-4 |
|
||||||||
1,183 10-5 |
|
1,183 10-5 |
|
7,045 10-7 |
|
7,045 10-7 |
|
3,237 10-5 |
|
||||||||
7,63 10-7 |
|
7,63 10-7 |
|
7,169 10-10 |
|
7,169 10-10 |
|
6,059 10-6 |
|
||||||||
2,746 10-8 |
|
2,746 10-8 |
|
1,851 10-14 |
|
1,851 10-14 |
|
9,546 10-7 |
|
||||||||
|
fE(t) = |
|
|
fEm(t)= |
|
fER(t) = |
|
|
|
fERm(t)= |
|
|
fGm(t) = |
||||
|
9,3 10-4 |
|
|
|
9,3 10-4 |
|
|
1,333 10-17 |
|
|
1,333 10-17 |
|
|
5,376 10-17 |
|||
|
7,968 10-4 |
|
|
7,968 10-4 |
|
1,09 10-9 |
|
|
|
1,09 10-9 |
|
|
|
2,501 10-9 |
|||
|
6,826 10-4 |
|
|
6,826 10-4 |
|
1,989 10-6 |
|
|
|
1,989 10-6 |
|
|
|
3,416 10-6 |
|||
|
5,848 10-4 |
|
|
5,848 10-4 |
|
9,555 10-5 |
|
|
|
9,555 10-5 |
|
|
|
1,349 10-4 |
|||
|
5,01 10-4 |
|
|
5,01 10-4 |
|
|
7,18 10-4 |
|
|
|
7,18 10-4 |
|
|
|
8,735 10-4 |
||
|
4,292 10-4 |
|
|
4,292 10-4 |
|
1,746 10-3 |
|
|
|
1,746 10-3 |
|
|
|
1,885 10-3 |
|||
|
3,677 10-4 |
|
|
3,677 10-4 |
|
1,987 10-3 |
|
|
|
1,987 10-3 |
|
|
|
1,941 10-3 |
|||
|
3,15 10-4 |
|
|
3,15 10-4 |
|
|
1,31 10-3 |
|
|
|
1,31 10-3 |
|
|
|
1,174 10-3 |
||
|
2,699 10-4 |
|
|
2,699 10-4 |
|
5,72 10-4 |
|
|
|
5,72 10-4 |
|
|
|
4,753 10-4 |
|||
|
2,312 10-4 |
|
|
2,312 10-4 |
|
1,811 10-4 |
|
|
|
1,811 10-4 |
|
|
|
1,407 10-4 |
|||
|
1,981 10-4 |
|
|
1,981 10-4 |
|
4,427 10-5 |
|
|
|
4,427 10-5 |
|
|
|
3,237 10-5 |
|||
|
1,697 10-4 |
|
|
1,697 10-4 |
|
8,757 10-6 |
|
|
|
8,757 10-6 |
|
|
|
6,059 10-6 |
|||
|
1,454 10-4 |
|
|
1,454 10-4 |
|
1,451 10-6 |
|
|
1,451 10-6 |
|
|
|
9,546 10-7 |
||||
91

Окончание прил. 3
5.2. Расчет по интегральным функциям: |
|
|
|
|
|
|
|
|||||||
|
|
FN(t)= |
|
hNm(t)= |
|
FW(t)= |
|
FWm(t) = |
|
hG(t) = |
||||
|
4734 10-6 |
|
4734 10-6 |
|
1,416 |
10-6 |
|
1,416 |
10-6 |
|
2,446 10-16 |
|||
|
1,236 10-4 |
|
1,236 10-4 |
|
2,674 |
10-4 |
|
2,674 |
10-4 |
|
3,395 |
10-8 |
||
|
1,857 10-3 |
|
1,857 10-3 |
|
3,926 |
10-3 |
|
|
3,926 |
10-3 |
|
9,148 |
10-5 |
|
|
0,016 |
|
0,016 |
|
0,024 |
|
|
0,024 |
|
6,4 10-3 |
||||
|
0,085 |
|
0,085 |
|
0,092 |
|
0,092 |
|
0,072 |
|||||
|
0,271 |
|
0,271 |
|
0,254 |
|
0,254 |
|
0,285 |
|||||
|
0,561 |
|
0,561 |
|
0,524 |
|
0,524 |
|
0,587 |
|||||
|
0,82 |
|
0,82 |
|
0,808 |
|
0,808 |
|
0,824 |
|||||
|
0,954 |
|
0,954 |
|
0,964 |
|
0,964 |
|
0,944 |
|||||
|
0,993 |
|
0,993 |
|
0,998 |
|
0,998 |
|
0,986 |
|||||
|
0,999 |
|
0,999 |
|
1 |
|
|
1 |
|
|
0,97 |
|||
|
1 |
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
||
|
1 |
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
||
|
|
FE(t) = |
|
hfcm(t)= |
|
FER(t) = |
FER.m(t) = FGm(t) = |
|
||||||
|
|
0,098 |
|
0,098 |
|
0 |
|
|
1,11 10-16 |
|
2,446 10-16 |
|||
|
|
0,227 |
|
0,227 |
|
1,433 |
10-8 |
|
1,433 |
10-8 |
|
3,395 |
10-8 |
|
|
0,338 |
|
0,338 |
|
5,123 |
10-5 |
|
|
5,123 |
10-5 |
|
9,148 |
10-5 |
|
|
0,433 |
|
0,433 |
|
4,32 10-3 |
|
|
4,32 10-3 |
|
6,4 10-3 |
||||
|
0,514 |
|
0,514 |
|
0,056 |
|
0,056 |
|
0,072 |
|||||
|
0,584 |
|
0,584 |
|
0,243 |
|
0,243 |
|
0,285 |
|||||
|
0,643 |
|
0,643 |
|
0,538 |
|
0,538 |
|
0,587 |
|||||
|
0,694 |
|
0,694 |
|
0,791 |
|
0,791 |
|
0,824 |
|||||
|
0,738 |
|
0,738 |
|
0,929 |
|
0,929 |
|
0,944 |
|||||
|
0,776 |
|
0,776 |
|
0,981 |
|
0,981 |
|
0,986 |
|||||
|
0,808 |
|
0,808 |
|
0,996 |
|
0,996 |
|
0,997 |
|||||
|
0,835 |
|
0,835 |
|
0,999 |
|
0,999 |
|
1 |
|
||||
|
0,859 |
|
0,859 |
|
1 |
|
|
1 |
|
|
1 |
|
||
92

Приложение 4
Проверка гипотез о характере закона распределения
Проверка гипотезы о том, что полученные экспериментально значения данных соответствуют ожидаемым значениям, вычисленным на основе некоторой модели, проводится с помощью критерия 2.
Для правильного применения критерия необходимо, чтобы каждое ожидаемое значение было бы не меньше 5 и сумма наблюдаемых значений должна равняться сумме ожидаемых.
Объем информации N:= 100. Полученный вектор сортируется в порядке возрастания и определяется вероятность возникновения рХ при каждом наработке:
Х:= sort(X); i:= 0.. N – 1; рХ:= (i+1)/(N+0.001).
Рассчитываются значения наработок, соответствующих вероятности рХ для нормального закона распределения XN, закона распределения Вейбулла XW, гамма распределения XG, экспоненциального закона распределения ХЕ, закона распределения Эрланга ХЕr, с использованием функции квантилей законов распределения:
XN:=qnorm (pX, tср, ); XW:= a-qweibull(pX, b); XG:= (1/ ) qgamma (pX, ); ХЕ:= qexp (pX, ).
Определяются суммы перечисленных векторов, они не должны значительно отличаться:
X:= 96990.93; XN:= 97828.127; XW:= 98176.339;
XE:= 105027.979; XG:= 97963.064.
Требуемый уровень значимости :=0.15.
Число степеней свободы := lenpth(X) – I; = 99. Рассчитываются оценки для указанных законов распределения:
2 |
: u uN 2 |
– для нормального закона распределения; |
|||
|
|
|
uN |
|
|
2 |
|
N 1 |
u uW |
2 |
|
1 |
: |
i |
i |
– для закона распределения Вейбулла; |
|
|
|
i 0 |
uWi |
|
|
|
|
22 |
: u uG 2 – для гамма–распределения; |
||
|
|
|
|
uG |
|
23 : |
u uE 2 |
– для экспоненциального закона распределения. |
|||
|
|
uE |
|
|
|
93

Окончание прил. 4
Вероятностьсовпаденияопытныхданныхсрасчетнымипокритерию 2: P( 2 >= 0цeнкa 2), допустимая вероятность 10%:
Р:= 1 – pchisq ( 2, )
Рј= |
|
i2 χ |
0,475 |
|
99,208 |
0,985 |
|
71,088 |
|
|
|
9,437 10-14 |
|
240,254 |
0 |
|
1,416-105 |
Значение 2, соответствующее заданному :
Х2:=qchisq (l- , ); X2:= 128.382.
Если Х2 < 2, то исходная гипотеза |
Х2< 2= |
|
0 |
|
|||
должна быть отвергнута: |
|
0 |
|
|
|
|
1 |
|
|
|
1 |
94

Приложение 5
Построение гистограммы распределения и кривых дифференциальных функций законов распределения
Выбор закона распределения можно произвести визуально, сравнивая гистограмму распределения и кривую плотности распределения.
Исходные данные о наработке приведены в прил. 3 (вектор X). Число данных, их среднее и среднеквадратичное отклонение определяются по выражениям:
N:= length (X); |
N:= 100; |
|||
tсp:=mean(X); |
tсp:=969.909; |
|||
:=stdev(X); |
|
N |
|
σ = 196.417. |
|
N 1 |
|||
|
|
|
||
Число интервалов гистограммы определяется по формуле ng:= ceil(l+3.31n(N)); ng = 25.
Минимальное и максимальное значения случайной величины в статистическом ряду определяются с помощью соответствующих функций векторов:
Xmin:= floor(min(X)); Xmax:=ceil(max(X)).
Величина интервала h:= (Xmax – Xmin)/ng.
Значение случайной величины, соответствующей началу j-го интервала:
j:=0…ng; Xint:=Xmin + hj;
k:= 0…ng – l.
Далее создается вектор с числом попаданий случайных величин, содержащихся в массиве Х,в интервал между j -м и (j+1)-м элементами вектора Xint:
F:= hist (Xint, X).
В заключение строится гистограмма и кривая дифференциальной функции для вышеперечисленных законов распределения. На основании полученных графиков делается вывод о законе распределения случайной величины.
95

Продолжение прил. 5
График плотности нормального распределения fN(x):= Nhdnorm (x,tср, )
fN(x) 20
10 |
|
|
|
|
|
|
|
0 400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
х |
График плотности распределения Вейбулла
FW(x):= Nh(1/ ) dweibull (x/a, b)
fN(x) |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
0 400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
х |
График плотности гамма-распределения
|
|
|
|
fG(x):= Nh dgamma(x , ) |
|
|
|
|||
fN(x) |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
х |
|
400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
|||
96
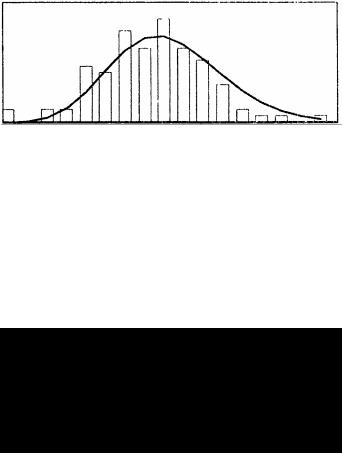
Окончание прил. 5
График плотности экспоненциального распределения
FE(x):= Nh dexp (x, )
fE(x) 20
10 |
|
|
|
|
|
|
|
0 400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
х |
График плотности распределения Эрланга
|
n 1 |
e e |
x |
fER(x):= Nh |
e( ex) |
|
|
|
(n 1)! |
|
|
fER(x) 20
10 |
|
|
|
|
|
|
|
0 400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
х |
97
Приложение 6
Характеристика условий эксплуатации подвижного состава [4,8]
|
|
|
|
|
|
Условия движения |
|
|
|
|
|
|
||||
|
за пределами |
|
в малых городах |
|
в больших |
|
||||||||||
|
|
пригородной |
|
(100000 ÷åë.) è â |
|
городах |
|
|
||||||||
|
|
çîíû |
|
|
пригородной зоне |
|
|
|
|
|
|
|||||
Тип дорожного |
|
|
|
|
|
|
рельеф местности |
|
|
|
|
|
|
|||
|
|
слабохолмистый, холмистый |
|
|
|
|
слабохолмистый, холмистый |
|
|
|
|
слабохолмистый, холмистый |
|
|
|
|
покрытия |
равнинный |
|
|
|
|
равнинный |
|
|
равнинный |
|
|
|
|
|||
|
|
гористый |
горный |
|
гористый |
горный |
|
гористый |
|
горный |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Цементобетон, |
1 |
|
1 |
2 |
3 |
|
2 |
2 |
2 |
3 |
3 |
|
3 |
3 |
|
3 |
асфальтобетон, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
брусчатка, мозаика |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Битумоминеральные |
2 |
|
2 |
2 |
3 |
|
2 |
3 |
3 |
3 |
3 |
|
3 |
3 |
|
4 |
смеси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Щебень, гравий, |
2 |
|
2 |
3 |
3 |
|
3 |
3 |
3 |
3 |
3 |
|
3 |
4 |
|
4 |
дегтебетон |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Булыжник, колотый |
3 |
|
3 |
3 |
3 |
|
3 |
3 |
3 |
3 |
3 |
|
4 |
4 |
|
4 |
камень, грунт и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
малопрочный камень, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обработанные вяжущими |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
материалами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Грунт, укрепленный или |
4 |
|
4 |
4 |
4 |
|
4 |
4 |
4 |
4 |
4 |
|
4 |
4 |
|
4 |
улучшенный местными |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
материалами, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бревенчатое покрытие |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Естественные грунтовые |
5 |
|
5 |
5 |
5 |
|
5 |
5 |
5 |
5 |
5 |
|
5 |
5 |
|
5 |
дороги, временные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
карьерные, отвальные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дороги, подъездные пути |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
без твердого покрытия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
98

Приложение 7
Коэффициент корректирования нормативов в зависимости от дорожных условий эксплуатации К1 [4, 8]
Показатель |
|
Категория условий эксплуатации |
|
||
|
1 |
2 |
3 |
4 |
5 |
Периодичность ТО |
1,0 |
0,9 |
0,8 |
0,7 |
0,6 |
Пробег до КР автомобилей |
1,0 |
0,9 |
0,8 |
0,7 |
0,6 |
Пробег до КР двигателей |
1,0 |
0,9 |
0,7 |
0,6 |
0,5 |
Удельная трудоемкость ТР |
1,0 |
1,1 |
1,2 |
1,4 |
1,5 |
Расход запасных частей |
1,0 |
1,1 |
1,25 |
1,4 |
1,65 |
Приложение 8 Коэффициенты корректирования нормативов
в зависимости от климатического района К 3.1 [4, 8]
|
|
|
Природно-климатический район |
|
|||
Показатель |
умеренный |
|
теплыйумеренный, теплыйумеренный |
теплый,влажный влажный |
,сухойжаркийочень сухой,жаркий |
холодный |
холодныйочень |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,9 |
|
|
Периодичность ТО |
|
1,0 |
|
1,0 |
0,9 |
0,8 |
|
Пробег до КР |
|
1,0 |
|
1,1 |
0,9 |
0,8 |
0,7 |
Удельная трудоемкость |
|
1,0 |
|
0,9 |
1,1 |
1,2 |
1,3 |
Расход запасных частей |
|
1,0 |
|
0,9 |
1,1 |
1,25 |
1,4 |
Приложение 9
Коэффициент корректирования нормативов в зависимости от модификации подвижного состава и организации его работы, К2 [4, 8]
Модификация подвижного состава |
|
Показатель |
|
|||
|
|
|
|
пробег |
трудоемкость ТО, |
расход |
|
|
|
|
до КР |
ТР |
запасных |
|
|
|
|
|
|
частей |
Седельные тягачи |
|
|
0,95 |
1,1 |
1,05 |
|
Автомобили с одним прицепом |
|
0,9 |
1,15 |
1,1 |
||
Автомобили с двумя прицепами |
|
0,85 |
1,2 |
1,2 |
||
Автомобили-самосвалы |
|
|
0,85 |
1,15 |
1,2 |
|
Автомобили |
самосвалы |
с |
одним |
0,8 |
1,2 |
1,25 |
прицепом при работе на коротких плечах |
|
|
|
|||
(5 км) |
|
|
|
|
|
|
Автомобили-самосвалы |
с |
двумя |
0,75 |
1,25 |
1,3 |
|
прицепами |
|
|
|
|
|
|
99
Приложение 1 0
Коэффициент корректировки трудоемкости ТО и ТР
взависимости от общего количества
иколичества технологически совместимых групп подвижного состава К5 [4, 8]
Количество автомобилей |
Количество технологически |
||||
на предприятии |
|
совместимых групп |
|
||
|
до 3 |
|
3 |
|
более 3 |
До 100 автомобилей |
1,15 |
|
1,2 |
|
1,3 |
100-200 автомобилей |
1,05 |
|
1,1 |
|
1,2 |
200-300 автомобилей |
0,95 |
|
1,0 |
|
1,1 |
300-600 автомобилей |
0,85 |
|
0,9 |
|
1,05 |
Более 600 автомобилей |
0,8 |
|
0,85 |
|
0,95 |
Приложение 1 1
Коэффициент корректирования нормативов трудоемкости ТР
взависимости от пробега
сначала эксплуатации подвижного состава К4 [4, 8]
|
|
|
Отношение пробегов L/Lн |
|
|
||||
Тип подвижного состава |
до 0,25 |
от 0,25 до 0,50 |
от 0,50 до 0,75 |
от 0,75 до 1,00 |
от 1,00 до 1,25 |
от 1,25 до 1,50 |
от 1,50 до 1,75 |
от 1,75 до 2,00 |
более 2,00 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
Грузовые автомобили |
0,4 |
0,7 |
1,0 |
1,2 |
1,3 |
1,4 |
1,6 |
1,9 |
2,1 |
Автобусы |
0,5 |
0,8 |
1,0 |
1,3 |
1,4 |
1,5 |
1,8 |
2,1 |
2,5 |
Легковые автомобили |
0,4 |
0,7 |
1,0 |
1,4 |
1,5 |
1,6 |
2,0 |
2,2 |
2,5 |
100
