1242

3.5.Имитационные модели (ИМ)

3.5.1.Классификация моделей

Основные признаки классификации имитационных моделей приведены в табл. 13.

3.5.2. Задачи при составлении имитационной модели (ИМ)

Анализ системы управления, выявление ее структуры, вывод параметров.

Оценка степени влияния каждого из элементов СУ. Разработка компьютерных моделей СУ.

Разработка методологии компьютерного эксперимента.

81

Проведение собственно компьютерного эксперимента с управлеE нием переменными.

Модификация и обновление модели (если это можно и целесообразно).

3.5.3. Имитационное моделирование

Очень распространенным типом моделирования является имитационное моделирование. Это связано с тем, что большинство реальных объектов в силу сложности, дискретного характера функционирования отдельных подсистем не могут быть адекватно описаны с помощью только аналитических математических моделей.

Важно и то, что имитационная модель позволяет использовать всю информацию вне зависимости от формы ее представления и степени формализации.

Имитационные модели позволяют творчески, гибко использовать всю имеющуюся информацию об объекте.

Имитационная модель строится по образцу и в соответствии со структурой исходного объекта.

Имитационная модель может быть с фиксированными входными параметрами и внутренними параметрами. Это детерминированная имитационная модель. Если же входные параметры и параметры модели могут иметь случайные значения, то говорят о моделировании

вслучайных условиях, а модель может быть названа стохастической.

3.6.Моделирование процесса разработки решения

3.6.1.Виды работ при моделировании

1.Составление перечня всех элементов системы управления (подсистем, элементов и связей).

2.Учет издержек обращения по элементам системы управления (СУ) (каковы суммарные затраты средств).

3.Рассмотрение степени влияния каждого из элементов (Св в долях 1, от О до 1, например, Св1=0,6, а Св2=0,06. Влияние первого элемента надо учесть обязательно, а второго – можно не учитывать).

Например, в фирме функционируют три подразделения: конструкторы, производственники и маркетологи, можно оценить степень их влияния на общий результат деятельности фирмы.

а) традиционный подход: Ск = 0,3, Сп= 0,5, См= 0,2 б) нетрадиционный подход: Ск= 0,2, Сп= 0,3, См= 0,5.

82

4.Группировка взаимосвязанных элементов: оценка постоянного или переменного влияния элементов на всю систему управления.

5.Составление системы уравнений.

3.6.2. Общий вид уравнения моделирования.

Упрощенная операционная математическая модель имеет вид:

Е=f(xi, yi),

где Е – мера общей эффективности модели; f – функция, определяющая соотношение;

x– управляемые переменные, определяющие поведение системы;

уi – неуправляемые переменные, определяющие поведение системы. Управляемые переменные (хj) – факторы, на которые может

оказывать прямое влияние руководитель:

-численность работников;

-количество оборудования;

-используемые технологии и т.д.

Неуправляемые переменные (уi) – факторы, на которые руковоE дитель не может воздействовать прямо, а может влиять только косвенно:

-действия потребителей, поставщиков, конкурентов;

-установки государственных органов;

-законодательство и т.д.

3.6.3. Математическая модель принятия решения

Наиболее правомерной представляется следующая модель:

EV= Pj Wp, где EV – функция двух переменных;

Pj – вероятность исходов из альтернативы: успеха или неуспеха; Wj – ценность исходов.

Ру+Рн=1,

где Ру – вероятность удачного исхода; Рн – вероятность неудачного исхода.

83

3.6.4. Формализация решения

Формализация индивидуального решения. Существующие заE висимости между показателями отображаются математическими символами как функции без указания точной формы связи:

ЛПР < S0, Т, R /S, Z, О, A, F, К, Aopt

Известно Неизвестно

где S0 – проблемная ситуация;

Т — время для принятия решения;

R – потребные для принятия решения ресурсы;

S – множество альтернативных ситуаций, доопределяющих проE блемную ситуацию;

Z – множество целей, преследуемых при ПР; О – множество ограничений извне и изнутри;

А – множество альтернативных вариантов решения; F — функция предпочтения индивида;

К – критерий выбора наилучшего решения; Аор, оптимальное решение (наилучшее).

Формализация группового решения. В общем виде задача принятия группового решения представляется на основе формализования схемы:

ГПР* < Sp, T, R/S, Z, О, A, F(f), L, К, Aoph

Известно Неизвестно

Известно Неизвестно

где F(f) – функция группового предпочтения, зависящая от вектора индивидуальных предпочтений членов группы;

L – символ принципа согласовывания индивидуальных предпочтений для формирования группового предпочтения.

3.6.5. Математические правила принятия решений

Группа без использования численных значении вероятности исходов:

Правило максимакса (mахmах) – максимизация максимальных доходов, ЛПР идет на риск, игнорирует возможные потери и рассчитывает на максимальный доход (смелый подход). Критерий крайнего оптимизма, «верь в удачу».

84

Сл – способность преуспеть в новых Шл – скорые результаты и оценка личного вклада;

Рл – соблюдение баланса между риском и усилием.

Доверие при применении моделей Д=(О+У)/Р,

где Д – доверие; О – общность целей при моделировании;

У –уверенность в успехе; Р – риск при применении моделей.

3.6.7. Управленческие таблицы принятия решений

Эффективным способом облегчения принятия управленческого решения являются таблицы решений. Таблица решений является очень простым и доступным способом определения взаимоотношении между исходными данными, соответствующими действиями, людьми, программами и т.д. Таблицы решений удобны как для принятия простейших управленческих решений, так и для выбора соответE ствующего планового решения при наличии различных критериев и правил выбора.

Они могут служить также основой для анализа процессов и реE шений, с которыми приходится сталкиваться в чрезвычайных, экE стренных ситуациях.

Таблица решений состоит из двух частей: из перечня конкретных условий и из перечня тех действий, которые должны быть выполнены для каждого конкретного условия. Структура таблицы решений представлена в табл. 14.

Правила решения (1, 2...) устанавливают соответствие между условиями и действиями, которые должны последовать. Правила решения должны рассматриваться в последовательности, начиная от первого.

Проиллюстрируем пользование таблицей решений для простейE шего случая контроля хода строительства двух объектов. СоответE ствующая упрощенная таблица решений представлена в табл. 15.

Таблицы решений дают простую логическую схему связи управленческого решения или предпринимаемого действия с соответствующими событиями или изменениями, произошедшими в контролируемой органом управления сфере.

86

Т а б л и ц а 14

Структура таблицы решений

87

В таблице обозначено буквами «Д» наличие данного условия, буквой «Н» E отсутствие условия, знаком «X» E необходимое действие для данного УСЛОВИЯ или сочетания условий

3.6.8. Модели принятия решений в организации

Вышеприведенную таблицу решений не следует путать с матрицей решений, построение которой потребует от лиц. Принимающих решения (ЛПР) творческого мышления, знания особенностей уровней принятия решений в организации и специфики организации, опыта прогнозирования ситуаций, знания мотивации поведения людей и т.д.

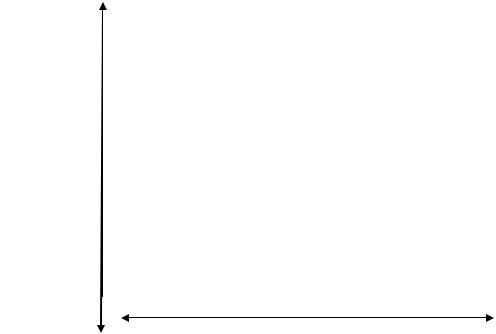
В зависимости от восприятия и интерпретации процесса принятия решения на различных уровнях можно выделить четыре модели принятия решений (рис. 20).

Рис. 20. Модели принятия решений

Рациональная модель (1) – выбор альтернатив с максимумом выгоды для организации. Связана с системным анализом и оценочными критериями.

Модель ограниченной рациональности – менеджер в принятии решений ограничен. Чем?

88

Личностно ограниченная – привычками и предубеждениями самого менеджера.

Удовлетворенность индивида (2) – трактуется как курс действий, который достаточно хорош для организации и требует минимума усилий со стороны членов организации.

ОрганизационноEограниченная – ресурсами, в том числе информацией в организации, сроками и другими возможностями организации.

Удовлетворенность организации (3) – трактуется как курс действий, который достаточно хорош для индивида и требует минимума затрат и усилий со стороны организации.

Политическая модель (4) – желание членов организации удовлеE творить в первую очередь индивидуальные интересы и потребности.

3.7. Типичные ошибки руководителя. Практические советы руководителю при моделировании

3.7.1.Типичные ошибки руководителя

1.Конечные цели моделирования неясны либо ошибочно кажутся очевидными.

2.Руководитель пытается держать под контролем все этапы и участников моделирования, не делегирует полномочия.

3.Руководитель пытается контролировать всю входную информацию и все выходные результаты.

4.Расходы на обучение персонала, зарплату консультантов и экспертов сведены к минимуму.

5.Усложняется проблема сбалансированности и проE порциональности задач при подготовке моделей.

6.Путаница с критериями построения модели.

7.В моделировании на первое место ставится форма, а не содержание и т.д.

3.7.2. Практические советы руководителю при моделировании

1.Определить систему необходимых и взаимосвязанных внешних

ивнутренних переменных.

2.Определить временные рамки действия модели.

3.Ориентировать модель на конечный результат.

4.Привлечь современное и качественное оборудование и программное обеспечение.

89