1133

Угол считается положительным ( 0) , если наблюдатель, глядя

со стороны острия оси Oz, видит тело вращающимся против хода часовой стрелки.

5. Угловые скорости и ускорения тела

По определению, угловой скоростью тела называется величина

Угловая скорость положительна, если тело вращается против хода часовой стрелки для наблюдателя, смотрящего на острие оси Оz.

Угловым ускорением называется величина

6. Закон равнопеременного вращения тела

По определению этого вида движения

const,

т.е.

d 22 . dt

Общие интегралы этого уравнения имеют вид

t c1,

t2 c1t c2 , 2

где c1 , c2 – постоянные интегрирования. Они находятся из начальных условий – при t t0 : 0 , 0. Используя последние, приходят к закону вращения тела в виде

t 2t0 2 0 t t0 0 .

31

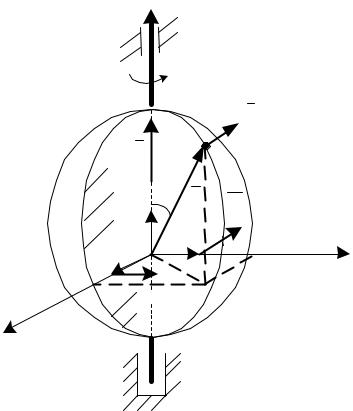
Угловая скорость вращения равна:

t t0 0 .

Здесь отмечается полная аналогия с формулами, характеризующими закон и скорость равнопеременного прямолинейного движения материальной точки (см. лекцию №2).

7. Вектор скорости точки тела при вращении. Формула Эйлера

Пусть ось вращения тела совпадает с осью Оz декартовой системы координат. Причем, эта система жестко связана (спаяна) с вращающимся телом (рис.3.5).

Рис. 3.5

Положение любой точки М тела можно описать радиусом-вектором r r xi yj zk.

Скорость точки определяется в результате дифференцирования r по времени

ddtr x dtdi y dtdj z dkdt .

32

При дифференцировании здесь принято во внимание, что координаты точки М в локальной системе не изменяются со временем. Производные di / dt , dj / dt определяют скорости точек А и В (концов соответствующих

где – модуль угловой скорости тела. Производная dk / dt 0 , т.к. ни модуль орта k , ни его направление не меняются во времени.

Тройка ортов i, j, k обладает следующими свойствами:

Принимая во внимание эти соотношения, формулу для скорости можно переписать в виде

x k i y k j 0 k k xi yj zk .

Следовательно,

k r .

Определение 3. Вектор k называется вектором угловой

скорости. Его направление совпадает с направлением орта к.

Правило знаков. Вектор положителен (совпадает с направлением оси Оz), если наблюдатель, глядя со стороны острия оси Оz (сверху), видит вращение тела против хода часовой стрелки.

Окончательно скорость любой точки вращающегося тела определяется по формуле

носящей имя Эйлера.

Очевидно, линейная скорость точки тела при вращении направлена перпендикулярно плоскости, образованной векторами и r . Как

известно, векторное произведение можно представить через определитель

* Цифры над символами внутри определителя указывают на порядок умножения элементов при вычислении положительных членов определителя.

33

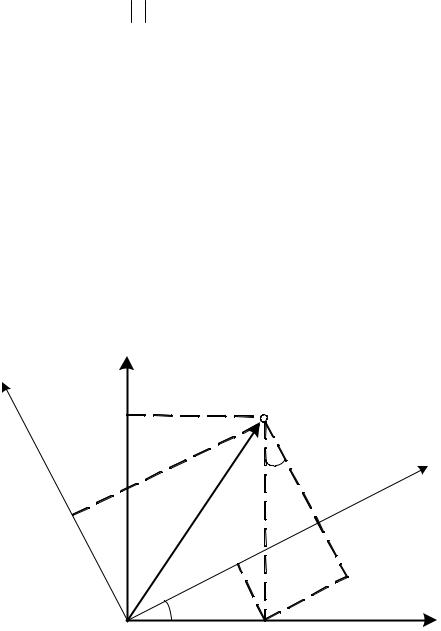
а его модуль равен:

r sin ,r ,

где r sin ,r – проекция радиуса-вектора r на плоскость, перпендикулярную оси Оz.

8.Матричная формула скорости

Копределению скорости тела при вращении можно подойти с иной точки зрения. Она состоит в изучении вращения тела с позиций теории преобразований систем координат (см. прил.).

Прежде всего, следует установить:

а) матричную форму закона вращения. С этой целью рассмотрим движение тела в двух системах координат: в неподвижной системе, оси которой обозначим греческими буквами О , и в подвижной, или

локальной, – Oху, связанной с вращающимся телом (рис. 3.6).

В начальном состоянии оси координат обеих систем совпадают. Положение произвольной точки М тела характеризуется радиусом-век- тором r , фиксированным в локальной системе координат, и, одновременно, вектором – в неподвижной (абсолютной). Вращение тела

в абсолютной системе по ходу часовой стрелки можно рассматривать как движение в обратном направлении связанной системы координат (см. приложение ). Координатами точки М в неподвижной системе координат

34

являются M и M . В локальной системе они обозначаются через xM и yM . Очевидно, что

xM OB OA AB,

где

OA M cos , AB M sin .

Следовательно,

xM M cos M sin .

Аналогично,

yM BM BD DM , yM M sin M cos .

Подчёркнутые зависимости можно объединить в одно соотношение, представив их в матричном виде*

характеризующую поворот системы координат Oху на угол против хода часовой стрелки, и вектор-столбцы радиусов-векторов**:

rx x, y T ,

y

, T .

б) Скорость любой точки тела на основе преобразования поворота определяется путём дифференцирования выражения (3.5):

*Данные преобразования подробно рассматриваются в математике [2].

**Индекс М в обозначениях компонент данных векторов опушен.

35

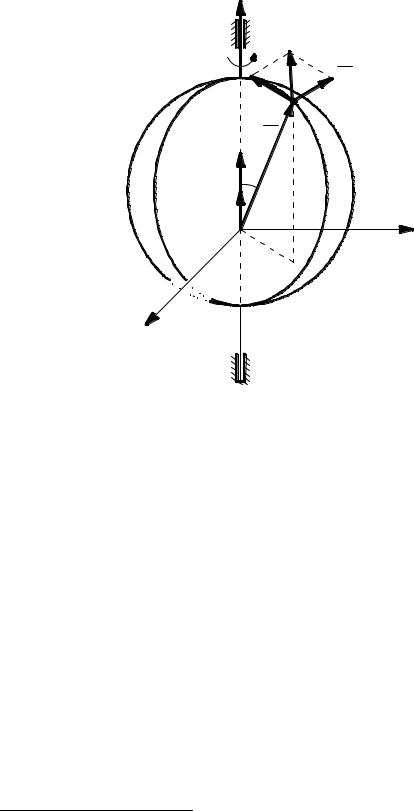
С учётом указанных определений вектор ускорения принимает вид a r .

x

Рис. 3.7

Воспользовавшись ещё раз формулой Эйлера, ускорение можно переписать в форме

a r r .

Вектор

a r

называется касательным ускорением,

а вектор

an r

– нормальным (центростремительным) ускорением* (рис. 3.7). Модуль ускорения an с учётом определения двойного векторного произведения

равен an 2 , где r sin .

Таким образом, формулу для ускорения а можно представить в виде a a an.

*Вектор a направлен по касательной к окружности радиуса , проходящей через точку М, а вектор an – по радиусу к оси вращения.

37

Контрольные вопросы

1.Какое движение тела называется поступательным?

2.Перечислите основные способы описания поступательного движения

тела.

3.Сформулируйте теорему о скоростях точек при поступательном движении.

4.Дайте определение вращательного движения тела.

5.Запишите закон равнопеременного вращения тела.

6.Сформулируйте правило знаков для вектора угловой скорости.

38

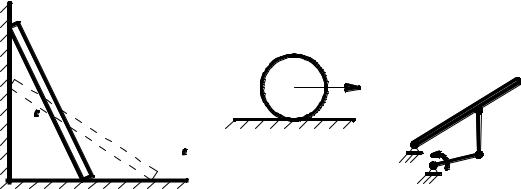
Лекция № 4. ПЛОСКОПАРАЛЛЕЛЬНОЕ (ПЛОСКОЕ) ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

1. Примеры и определение плоского движения

Рассматривая движение сползающей лестницы, качение катка по земле, движение звена 2-3 механизма открывания двери (рис. 4.1), можно обнаружить общее свойство этих движений – любая точка каждого из этих тел движется в одной плоскости.

Рис. 4.1

Определение 1. Движение тела, при котором любая точка тела перемещается в плоскости, параллельной некоторой неподвижной плоскости, называется плоскопараллельным (плоским).

О плоском движении твердого тела V можно судить по движению плоской фигуры, полученной в результате пересечения тела плоскостью Q,

параллельной неподвижной плоскости Р (рис. 4.2,а). Действительно,

возьмем любую точку а, лежащую в плоскости Q, и опустим из нее перпендикуляр аА на неподвижную плоскость. Прямая аА, ассоцииро-

ванная с жестким стержнем, при плоском движении тела, очевидно, совершает поступательное движение. В соответствии с теоремами о равенстве скоростей и ускорений при поступательном движении тел и подобии траекторий, любая точка стержня аА обладает одной и той же

скоростью и ускорением и движется по одинаковой траектории. Таким образом, ввиду произвольного выбора точки а плоское движение тела можно охарактеризовать параметрами движения плоского сечения Q или его следа S на неподвижной плоскости Р (рис. 4.2,б).

39

rB t rA t AB;

40