1130

3. Определение главных центральных моментов инерции относительно главных центральных осей.

Ix Ix1 Ix2 Ix3

Ix1 Ix11 a12 A 1 0,0152 0,25632 0,96 0,1143 м4

Ix2 Ix22 a22 A 2

0,002807 (0,2302 0,2563)2 0,2513 0,06229 м4

Ix3 Ix33 a32 A 3 0,0072 (0,6 0,2563)2 0,3600 0,04973 м4

Ix 0,1143-0,06229 0,04973 0,10174 м4

I y I y1 I y2 I y3 0,1152 0,011005 0,0216 0,12675 м4

Пример1.3. Определитьположениеглавныхцентральныхосей ивычислитьзначениеглавныхцентральныхмоментовинерциифигуры, изображенной на рис. 1.3.

Разбиваем сложную фигуру на две простые, геометрические характеристики и координаты центров тяжести которых известны:1 – прямоугольный треугольник, 2 – четверть круга.

11

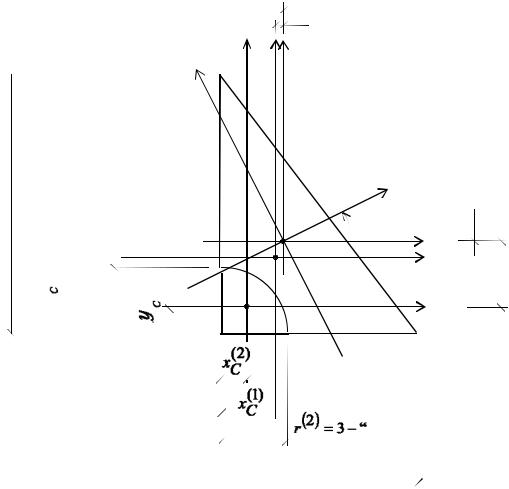
ХС = b2 b1

Y у2 у1 у

Рис. 1.3

Наименования осей и обозначения принимаются в соответствии с принятыми на рис. 1.3.

1. Определениеположенияцентратяжестисечения. Вычисляемстати-

ческий момент площади сечения относительно вспомогательных осей. Для сложного сечения статический момент равен алгебраической сумме статических моментов частей, его составляющих. Так как четверть круга представляет собой вырез (отверстие), то статический момент и площадь второй фигуры надо вычесть из первой:

Расположениевспомогательнойсистемыкоординатможет бытьразличным. В данном примере в качестве неё используем центральные оси второй фигуры x2 и y2, тогда

xс 36 (2 1,27) 7,07 0 0,908 см; 36 7,07

yс 36 (4 1,27) 7,07 0 3,40 см. 36 7,0

Наносим на чертёж центр тяжести и центральные оси х и y

(рис. 1.3).

2. Определение моментов инерции относительно центральных осей.

Моменты инерции всего сечения относительно центральных осей вычисляются как алгебраическая сумма моментов инерции простых фигур относительно этих осей. При этом значения моментов инерции для четверти круга принимаем со знаком минус, так как данная фигура представляет собой вырез (отверстие):

Ix Ix(1) Ix(2) ; I y I y(1) Ix(2) ; Ixy Ixy(1) Ixy(2).

Для определения значений моментов инерции первой и второй фигур относительно центральных осей всего сечения x и y используем соотношения:

13

3. Определение положения главных центральных осей и вычисление главных центральных моментов инерции. По найденным значениям момен-

тов инерции относительно центральных осей вычисляем угол 0 поворота главных центральных осей (см. рис. 1.3):

Поворачивая центральные оси сечения x и y на угол 24,4 против часовой стрелки, строимглавныецентральныеосиХ, У.

На основе зависимостей (1.8) определяем значения главных центральных моментов инерции сечения:

I X Ix cos2 0 I y sin2 0 Ixy sin 2 0

=218 cos2(24,4 ) + 62,8 sin2(24,4 ) – (– 88,2) sin(48,8 ) =

=180,9 + 10,7 + 66,2 = 257,8 см4;

IY Ix sin2 0 I y cos2 0 Ixy sin 2 0

= 218 sin 2(24,4 ) + 62,8 cos 2(24,4 ) + (– 88,2) sin(48,8 ) = = 37,0 + 52,1 – 66,2 =22,9 см4.

Таким образом, экстремальные значения главных центральных моментов инерции сечения равны следующим величинам:

Imax = IX = 257,8 см4; Imin = IY = 22,9 см4.

Для проверки правильности последних вычислений используем соотношения:

Ix Iy IX IY ; 218 + 62,8 = 257,8 + 22,9; 280,8 см4 280,7 см4.

14

Тема №2 ОСЕВОЕ РАСТЯЖЕНИЕ (СЖАТИЕ) БРУСА

Примеры решения задач

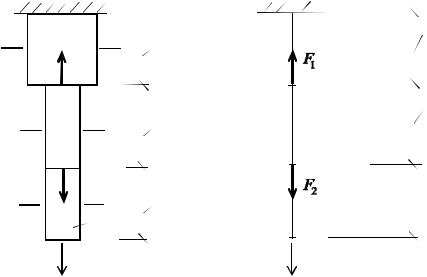
П р и м е р 2.1. Определить площадь поперечного сечения A и перемещение нижнего конца стержня l при R 210МПа и E 200 ГПа (рис.

2.1). с 1,0 ; f 1,1.

Решение

1. Вычисление расчётных нагрузок.

F1p F1н f 50 1.1 55 Кн;

F2p F2н f 30 1.1 33 Кн

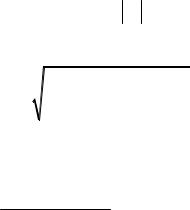
2. Построение эпюр продольных сил и напряжений. Имеем три участка:

AB , BC , CD . Для построения эпюр воспользуемся методом сечений. Последовательно проводим сечения на каждом участке стержня: 1-1, 2-2, 3-3 (рис. 2.1, a). Рассматриваем равновесие нижних отсеченных частей стержня (рис. 2.2). Во всех сечениях за положительное значение принята растягивающая сила, направленная от сечения.

15

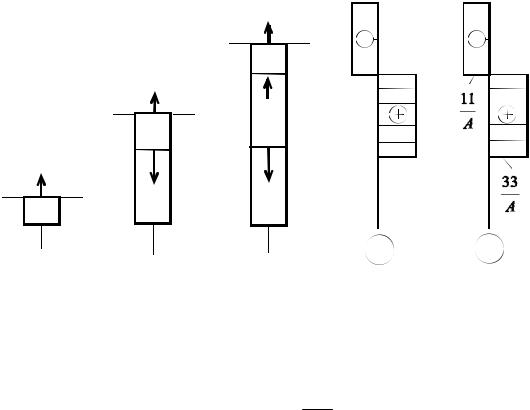
На участке AB , в сечении 3-3 (рис. 2.2, в):

Рис. 2.2

Из эпюры нормальных напряжений z (рис. 2.2, д) следует, что все се-

чения на участке BC равнопасны, поскольку именно на этом участке возникают наибольшие по величине нормальные напряжения:

max (2) 33 Кн2 . A см

16

3. Подбор поперечного сечения. Из условия прочности определяем требуемую площадь поперечного сечения:

2А 3,2 см2 .

4. Проверка прочности сечения. Прочность сечения проверяем на каждом участке стержня.

Участок АВ:

Участок ВС :

Таким образом, на всех участках условие прочности выполняется. Это означает, что площадь поперечного сечения подобрана, верно.

5. Определение перемещения нижнего сечения стержня. Перемещение точки D определяем относительно опорного неподвижного сечения, то есть, находим абсолютную деформацию участка AD как алгебраическую сумму деформаций на каждом из трех участков:

lAD lAB lBC lCD .

Деформации на каждом участке вычисляем по формуле с учётом знака продольной силы. При этом учтём понижающий коэффициент для продольнойсилы, обеспечивающийрасчётдеформацийпонормативнымнагрузкам.

lCD 0 .

Полная деформация стержня будет равна

lAD lAB lCD 0,625 1,87 0 1,245мм.

17

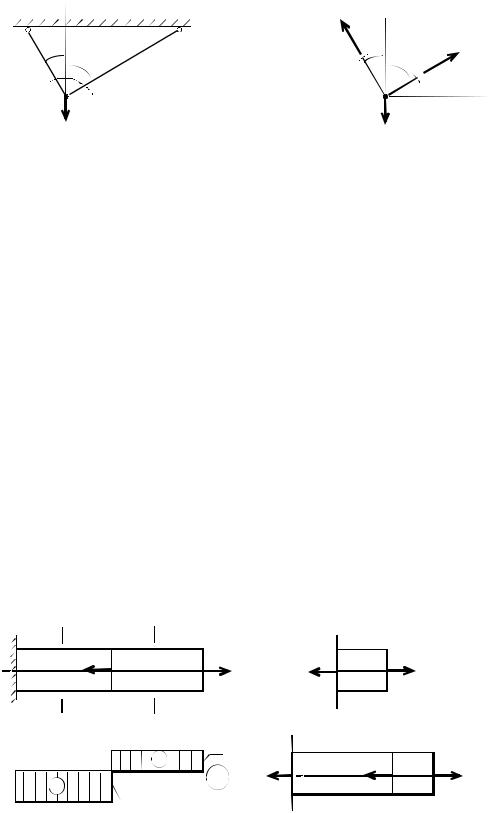
Примеры решения задач

П р и м е р 2.2. Подобрать поперечное сечение стержней, если R= 180

МПа (рис. 2.3).

Рис. 2.3

Решение

1.Определение внутренних усилий в стержнях. Для этого вырезаем узел

A и составляем уравнения равновесия (рис. 2.3, б):

x =0, – N1 sin30 + N2 sin60 = 0, N1 = N2 0,8660,5 = 1,732 N2;

y =0, N1 cos30 + N2 cos60 – F = 0, N1 = 500 0,5N2 . 0,866

Решая эти уравнения совместно, получим:

N2 = 250 кН, N1 = 433 кН.

2. Определение площади поперечного сечения. Из условия прочности находим требуемые площади:

П р и м е р 2.3. Для стержня диаметром D = 4 см определить допускаемую величину силы F при R = 160 МПа (рис. 2.4, а).

Рис. 2.4

18

Решение

1. Построение эпюры продольных сил. В сечении 1-1 (рис. 2.4, б)

N1–F = 0; N = F1 (растяжение). В сечении 2-2 (рис. 2.4, в) N2–F + 3F = 0; N2 = –2F (сжатие). Максимальное усилие Nmax= 2F.

2. Определение допускаемой величины силы. Из условия прочности мак-

симальное продольное усилие, которое можно допустить в поперечном сечении, равно:

Nmax = R·A = 160 106 3,14 42 10 4 = 200960 Н = 201,96 кН. 4

В сечении действует усилие 2F. Тогда допускаемая сила

F N2max 201,962 100,98 кН.

Тема №3

КРУЧЕНИЕ БРУСА КРУГЛОГО СЕЧЕНИЯ

Примеры задач П р и м е р 3.1. Известны внешние нормативные крутящие моменты,

C 0,8.

1.Вычисление расчётных нагрузок.

M B M Bн f 1 1,1 1,1 Кн м;

M С M Сн f 3,6 1,1 3,96 Кн м; M D M Dн f 1,5 1,1 1,65 Кн м.

2. Построение эпюры моментов начинаем со свободного конца балки. Последовательно проводим сечения на каждом участке стержня: I-I, II-II и III-III. и рассматриваем равновесие отсечённых правых частей.

На участке D C , в сечении I-I,

mZ T1н M Dн 0 , T1н M Dн 1,5 кН м.

На участке C B , в сечении II-II,

mZ T2н M Cн M Dн 0 , T2н M Dн MCн 1,5 3,6 2,1 кН м.

На участке A B , в сечении III-III,

19

mZ T3н M Bн MCн M Dн 0 ,

T2н M Bн MCн M Dн 1,5 3,6 1,0 1,1 кН м.

Моменты T2н и T3н получилисьотрицательными, этоозначает, чтоихис-

тинные направления противоположны принятым, т.е. будут направлены против часовой стрелки.

На участке A B , в сечении III-III,

mZ T3н M Bн MCн M Dн 0 ,

T2н M Bн MCн M Dн 1,5 3,6 1,0 1,1 кН м.

Моменты T2н и T3н получилисьотрицательными, этоозначает, чтоихис-

тинные направления противоположны принятым, т.е. должны быть направлены против часовой стрелки.

На эпюре моментов положительные моменты откладываем вверх, а отрицательные вниз (рис. 3.1). Эпюра расчётных крутящих моментов получается умножением нормативных значений на коэффициент надёжности по нагрузке f 1,1;

T1 T1н 1,1 1,5 1,1 1,65 кН м;

Т2 T2н 1,1 2,1 1,1 2,31 кН м;

Т3 T3н 1,1 1,1 1,1 1,21 кН м.

Из эпюры следует, что наибольший по величине расчетный крутящий момент действует на участке В С и равен

Тmax T2 2,31 кН м.

3.Определение диаметра стержня. Из условия прочности получаем:

Округливполученноезначение, принимаемдиаметрстержня d 60 мм. 4. Проверка прочности сечения. Проверяем условие прочности:

max 2,31 103 16 54,5 106 Па 100 106 0,8 Па, 3,14 603 10 9

54,5 МПа 80 МПа.

Условие прочности выполняется.

20