Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

152

.pdf

Скачиваний:

Добавлен:

16.06.2024

Размер:

205.6 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Пензенский государственный университет архитектуры и строительства»

(ПГУАС)

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ:

ЭЛЕМЕНТЫ ТЕОРИИ ОЦЕНОК И ПРОВЕРКИ СТАТИСТИЧЕСКИХ ГИПОТЕЗ

Методические указания по выполнению практических занятий

Под общей редакцией доктора технических наук, профессора Ю.П. Скачкова

Пенза 2014

УДК 517 ББК 22;161.1

М34

Методические указания подготовлены в рамках проекта «ПГУАС – региональный центр повышения качества подготовки высококвалифицированных кадров для строительной отрасли» (конкурс Министерства образования и науки Российской Федерации – «Кадры для регионов»)

Рецензент: доктор химических наук, профессор кафедры «Информационно;вычисли; тельные системы» А.Н. Кошев (ПГУАС)

Математическое моделирование: элементы теории оценок М34 и проверки статистических гипотез: метод. указания к практическим занятиям / А.М. Данилов, И.А. Гарькина; под общ. ред. д;ра техн. наук, проф. Ю.П. Скачкова. – Пенза:

ПГУАС, 2014. – 24 с.

Рассматриваются вопросы математического моделирования, имеющие приоритетное прикладное значение. Приводятся методы определения числовых значений характеристик и законов распределения наблюдаемых случайных пере; менных на основании ограниченного числа испытаний. Содержит контрольные вопросы и задания для самостоятельной работы.

Направлены на формирование способности демонстрировать знания фунда; ментальных и прикладных дисциплин ООП магистратуры; способности и готов; ности проводить научные эксперименты, оценивать результаты исследований; способности разрабатывать физические и математические модели явлений и объектов, относящихся к профилю деятельности.

Подготовлены на кафедре «Математика и математическое моделирование» и базовой кафедре ПГУАС при ЗАО «Спецстроймеханика» и предназначены для магистрантов, обучающихся по направлению 08.04.01 «Строительство», для вы; полнения практических занятий по дисциплине «Математическое модели; рование».

Пензенский государственный университет архитектуры и строительства, 2014

Данилов А.М., Гарькина И.А., 2014

1. ЭЛЕМЕНТЫ ТЕОРИИ ОЦЕНОК

Пусть X x – одномерная случайная величина. Рассмотрим n;

мерную случайную величину
		X1, X2 , , Xn ,	(1)
где Xi , i		являются независимыми случайными	величинами с
	1,n

одинаковыми функциями распределения вероятностей, совпадающими с функцией распределения X .

Функция распределения вероятностей такой многомерной вели; чины определится как произведение функций распределения вероят; ностей ее компонентов.

Случайные величины Xi удобно рассматривать как результаты не;

которого эксперимента. При этом многомерная случайная величина (1) может рассматриваться или как результат последовательного проведе; ния n независимых экспериментов на одной и той же эксперимен; тальной установке, или как результат проведения одновременных экспериментов на n однотипных экспериментальных установках.

Поскольку всегда имеется теоретическая возможность проводить неограниченное число экспериментов, то можно говорить о бесконеч; ном наборе случайных чисел xi c одинаковыми функциями распре; деления вероятностей.

Каждый конкретный результат эксперимента, а, следовательно,

каждое Xi	из конечного набора (1) может рассматриваться как выбор
одного из	чисел бесконечной совокупности. Набор x1, x2 , , xn

представляет собой n таких выборов и называется случайной выборкой. Основной задачей математической статистики является опреде; ление независимых параметров распределения бесконечной совокуп; ности по известной конечной выборке. При этом речь может идти или об определении самой функции распределения, или отдельных пара; метров функции распределения, таких как математическое ожидание, дисперсия, наименьшее или наибольшее значения случайной вели;

чины и т.п.

Поскольку элементы конечной выборки являются случайными величинами, то случайным будет и значение параметра, определенное с помощью этой выборки. В частности, если имеется несколько выборок одного и того же объема из одной и той же бесконечной совокупности, то каждая из них даст свое значение интересующего параметра. Поэто; му по конечной выборке нельзя судить о значении параметра, а можно лишь более или менее оценить этот параметр. Численные значения от;

дельных параметров, определенных из конечной выборки, называются

оценками параметров бесконечной совокупности.

В общем случае из одной и той же совокупности можно получить различные оценки a параметров а. Какая же оценка при этом будет предпочтительней? На этот вопрос можно ответить, если потребовать, чтобы оценка удовлетворяла некоторым требованиям.

Прежде всего, оценка должна быть состоятельной, т.е. с увеличе; нием числа испытаний (объема выборки) должна сходиться по вероят; ности к а, т. е. при n и любом > 0 должно выполняться

P( an a ) 1

где an – оценка параметра а, полученная по выборке объема n.

Оценка должна быть несмещенной, т.е. она не должна содержать систематической ошибки, преувеличивающей или преуменьшающей значение параметра для выборок. Это означает, что

M a a .

Наконец, оценка должна быть эффективной, т.е. в среднем иметь минимальный разброс.

D a min .

Из всех несмещенных и состоятельных оценок, таким образом, отдается предпочтение той, которая оказывается наиболее близкой к оцениваемому параметру, т.е. при которой большие отклонения при использовании различных выборов встречались бы как можно реже.

Различают два вида оценок: точечные и интервальные.

В первом случае интересуются одним значением (точкой), во вто; ром – интервалом значений, т.е. при интервальных оценках стараются определить вероятность того, что отклонение оценки параметра от истинного значения будет меньше заданного значения. Для определе; ния близости оценки к оцениваемому параметру вводят доверительный интервал близости , а саму близость оценивают по величине вероят; ности, которую называют доверительной вероятностью , и задают за; ранее p . Таким образом, задача оценки состоит в том, чтобы найти по экспериментальным данным несмещенную оценку an , удо; влетворяющую

P( an a ) .

Здесь интервал I an , an – доверительный.

1.1. Точечные оценки математического ожидания и дисперсии

Пусть x1, x2 , , xn – выборка из совокупности с математическим

ожиданием m и дисперсией				D 2 . Необходимо определить состоя;
тельные оценки m, D			соответственно для m и D.
Обычно за оценку m берут среднеарифметическое значение выборки
						1	n
				m		1	xi ,	(2)
				m			xi ,	(2)
						n i 1
называемое выборочным средним.
Из закона больших чисел
	n
	n
(		xi	m	1	при n и любом 0 )
(			m	1	при n и любом 0 )
	i 1 n

следует, что такая оценка является состоятельной.

Оценка (2) является и несмещенной. Действительно, выборочное среднее m представляет собой сумму случайных величин xni , поэтому

оно само будет случайной величиной. Тогда можно говорить о законе распределения выборочного среднего, его математическом ожидании и дисперсии.

Используя свойство математического ожидания, получим

nm m .

(3)

n i 1

i 1

n i 1

Таким образом, оценка m

является несмещенной.

Определим дисперсию D m .

Пользуясь независимостью x1 и свойствами дисперсии, получим

D m D

D x

(4)

n i 1 i

i 1 i

i 1

n n

Если выборка взята из совокупности с нормальным распределе; нием, то m , как сумма нормально распределенных случайных величин с учетом (3) и (4), также будет иметь нормальное распределение с плотностью вероятностей

f m	1			(m m)2 /2	D
	1		e	(m m)2 /2	n .

	D
	D	2

	n
	n

Можно показать,	что при этом D m	2	будет минимальной,
		n

следовательно, оценка (2) будет эффективной в смысле минимума дисперсии.

Перейдем к оценке дисперсии. Покажем, что оценки вида

	1	n
D		xi m	2	(5)

	n 1 i 1

является несмещенной оценкой дисперсии. Действительно,

x 2

(xi

n 1

n 1 i 1

n 1

2m2

n 1

xi 2

xi2

xi x j

n 1

x 2

n 1

i 1

Найдем математическое ожидание этой оценки

M x

i j

n 1

Выберем начало отсчета xi

в точке m. Тогда xi

M x i

x j 0,

xi x j

(6)

(7)

(8)

где знак над x означает центрирование. Последнее равенство спра; ведливо в силу независимости опытов.

Подставим (8) в (7), получим

	n	n		1	nD	D.
			2
M D	n 1	n

Таким образом, оценка (5) является несмещенной. Из (5) следует

		xi
		2
D	n	i	m2
		i		.
	n 1	n		.
	n 1	n

Величина m2	сходится по вероятности к m2. А	xi2	есть среднее
		n
	i

арифметическое n наблюденных значений случайной величины x2 .

Поэтому			xi2	по вероятности сходится к					2

								M x	2 x . Тогда
		i	n
	xi2	сходится по вероятности к 2 x m					2	D .
	n m2
i
	Так как множитель				n	1 при n ,	то D также сходится по

					n 1
вероятности к D, то есть оценка D является состоятельной.
	Отметим, что оценка D					для дисперсии не является эффективной.

Однако в случае нормального распределения она является асимпто; тически эффективной.

1.2. Оценка параметров по методу доверительных интервалов

Ниже рассматриваются точные методы оценки параметров случай; ной величины, подчиненной нормальному закону распределения. Основная идея этих методов состоит в том, что от исходной величины переходят к некоторой другой величине, распределение которой не зависит от параметров исходной случайной величины, а зависит только от вида ее закона распределения и числа измерений (объема выборки) n.

1.2.1. Определение доверительного интервала для дисперсии D

Воспользуемся известной из теории вероятностей теоремой: если xi – независимые случайные величины, подчиняющиеся стандартному нор; мальному распределению M xi 0, D xi 1 , то случайная величина

n
2 xi2	(9)

i 1

подчиняется распределению 2 c n степенями свободы (n – число независимых случайных величин в сумме (9)).

Плотность распределения случайной величины 2 по закону с n степенями свободы определяется формулой

(v)

A v 2

при v 0,

(10)

при v 0,

где

1/ 22

ux 1e

udu

(для гамма;функции Г(x) имеются таблицы)

Можно показать, что для случайной величины, распределенной по закону 2 с n степенями свободы, справедливо:

M v n,

D v 2n.

(11)

Пусть xi – нормально распределенные случайные величины и

D 2

xi m

n 1 i 1

несмещенная оценка дисперсии. Рассмотрим случайную величину

1 D

xi m

i 1

Таким образом,

V представляет собой сумму квадратов случайных

величин

xi m

, распределенных по нормальному закону. При этом

M xi M m

m m 0,

D xi

Однако среди этих n случайных величин независимых только n–1,

так как

n x

xi n

i 1

0 .

i 1

Поэтому случайная величина V представляет собой сумму квадра; тов n–1 случайных величин, удовлетворяющих условиям приведенной выше теоремы, и плотность ее распределения есть распределение 2 с n–1 степенями свободы.

Поэтому в соответствии с (11)

n 1 D

n 1,

а закон распределения V в соответствии с (10) имеет вид:

n 1

при v 0,

Kn 1

v An 1v 2

e 2

при v 0,

где

1 n 1

n 1

An 1

2 2

Попутно отметим,

что на этом примере очень четко иллюстри;

руется понятие числа степеней свободы. Группа законов распределе; ния, таких как 2 ;распределение, распределение Стьюдента и др., свя; зана с понятием n независимых случайных величин. Если они зависи; мы, то к ним не применима выше рассмотренная теорема и на первый взгляд не подчиняются этим законам распределения. Но если можно точно выявить связь (как в вышерассмотренном примере), то всегда за счет уменьшения числа величин можно добиться их независимости. Для этого при наличии l связей следует выразить любые l случайных величин через остальные n-l. Тогда исходная величина может быть представлена не как сумма n зависимых, а как сумма r=n-l незави; симых случайных величин, к которой можно применять теоремы, справедливые только для суммы независимых случайных величин.

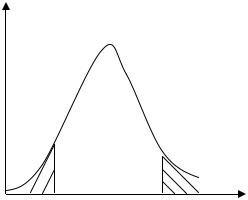
Поскольку закон распределения V известен, то можно всегда найти доверительный интервал, в который попадает эта величина с вероят; ностью . Трудности в построении этого интервала состоят в том, что2 ;распределение несимметрично (рис.1).

Поэтому условимся выбирать доверительный интервал I для V

при равенстве вероятностей выхода V влево и вправо за этот интервал (это означает равенство заштрихованных на рис.1 площадей величине

1 ). Заметим, 2 – вероятность непопадания V в интервал I . 2

Kn 1(v)

2	2	v 2
1	2

Рис. 1

Обычно в таблицах для случайных величин, распределенных по2 ;распределению, приводятся значения вероятности

p P V 2 F 2 .

Фрагмент такой таблицы приводится в приложении 1.

Для доверительного интервала (v1, v2) = 12, 22 должны иметь:

P V v1 , P V v2 .

Но P V v1 1 P V vi .

Поэтому v1 12 и v2 22 определяется из условий: 1 F 12 ,

F 22 .

Доверительный интервал для V n 1 D есть интервал

12 V 22.

Откуда

	2	n 1 D	2		,
1		D		2
или		D
или
1		D		1		,

	2	n 1 D		2
2				1

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.06.20242.05 Mб01515.pdf
#
16.06.20242.05 Mб01516.pdf
#
16.06.20242.05 Mб01517.pdf
#
16.06.20242.06 Mб01518.pdf
#
16.06.20242.07 Mб01519.pdf
#
16.06.2024205.6 Кб0152.pdf
#
16.06.20242.07 Mб01520.pdf
#
16.06.20242.07 Mб01521.pdf
#
16.06.20242.07 Mб01522.pdf
#
16.06.20242.07 Mб71523.pdf
#
16.06.20242.08 Mб01524.pdf