РВСС Распространение волн в случайных средах / Лекции / Импульс среднее поле

ИМПУЛЬС

Двухвременная матрица плотности

Матрица плотности в частотном представлении

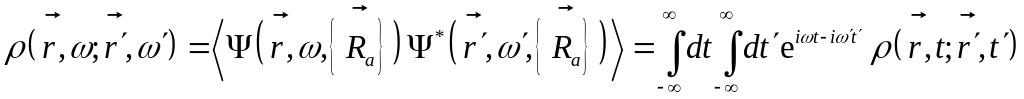
Характеристики света

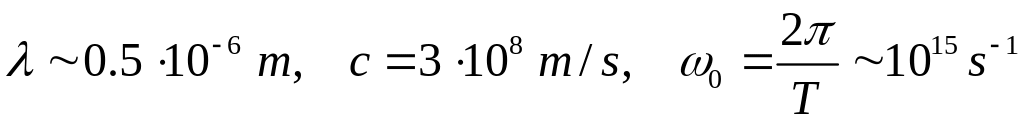
Длительность импульса

«Быстрая» и «медленная» временные переменные

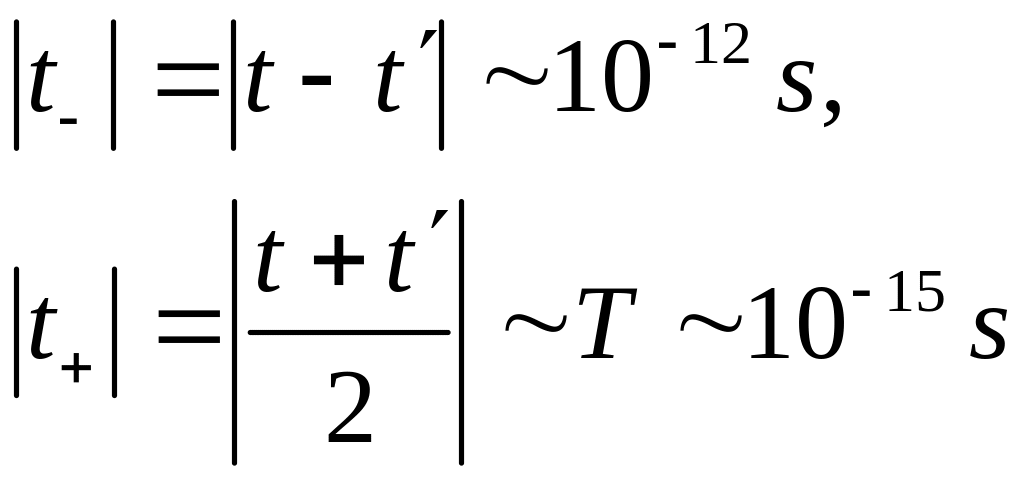
«Быстрая» и «медленная» частотные переменные

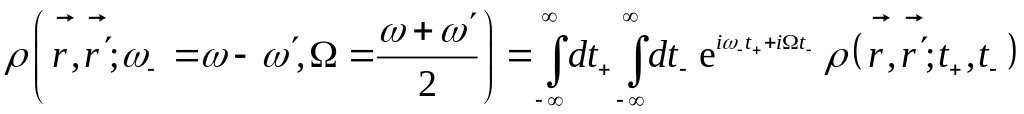
Надо получить уравнение для нестационарной матрицы плотности в представлении Вигнера

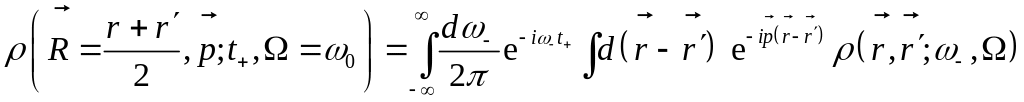
Будем работать со средними функцией Грина и двухчастотной матрицей плотности

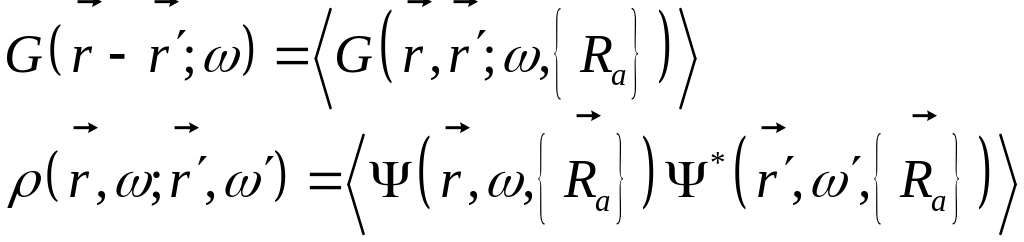
ВОЛНОВОЕ УРАВНЕНИЕ

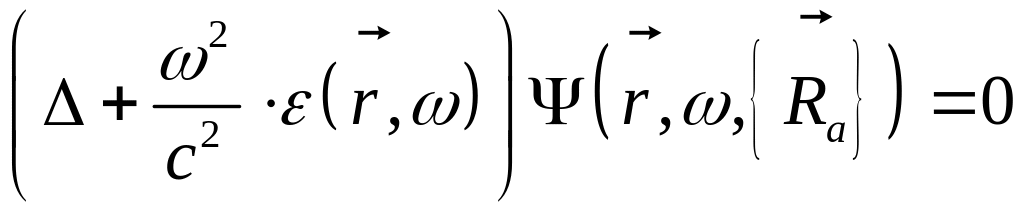
Случайная диэлектрическая проницаемость

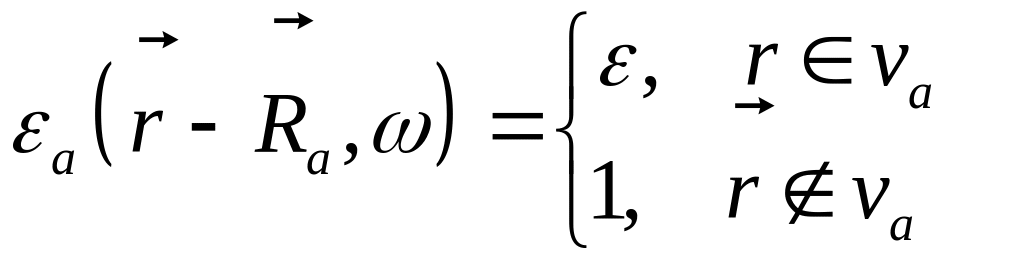
- «центр» -го рассеивателя, - объём, занимаемый -ым рассеивателем

Другая форма записи диэлектрической проницаемости

Поле - случайная функция координат рассеивателей

Уравнение, с которым будем работать

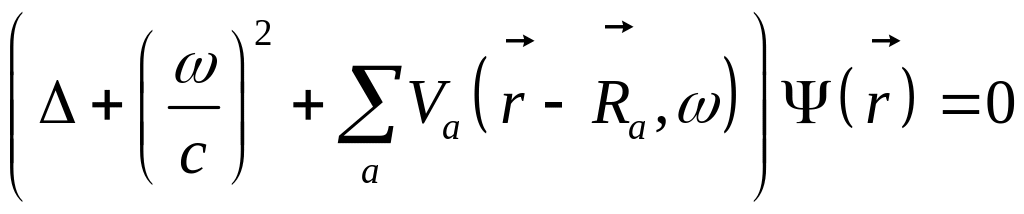
где

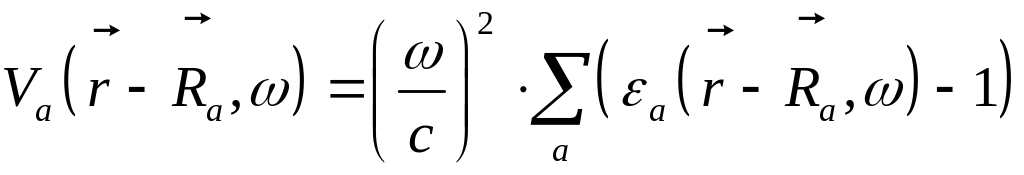
Конечная цель – матрица плотности, усреднённая по расположению рассеивателей

Модель разреженной среды с некоррелированными рассеивателями

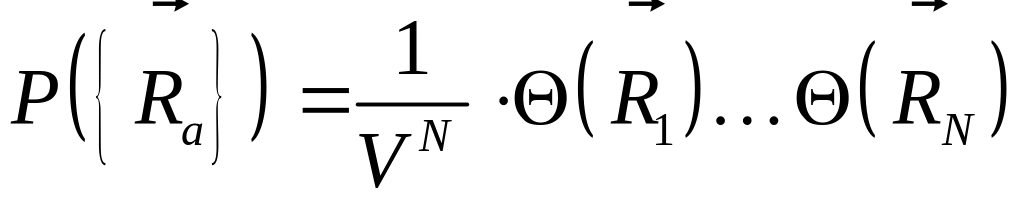
Пример: усреднить

Ответ

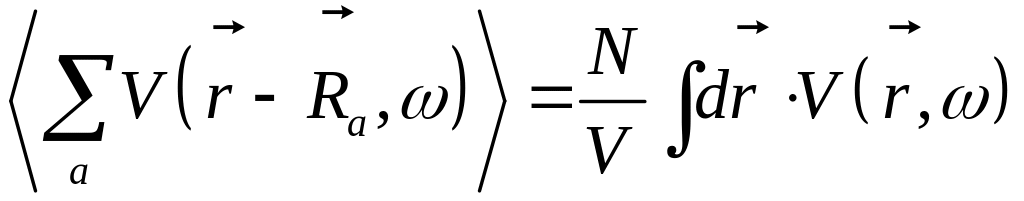
Интегральное уравнение для функции Грина

Символическая запись

Первая и вторая итерации

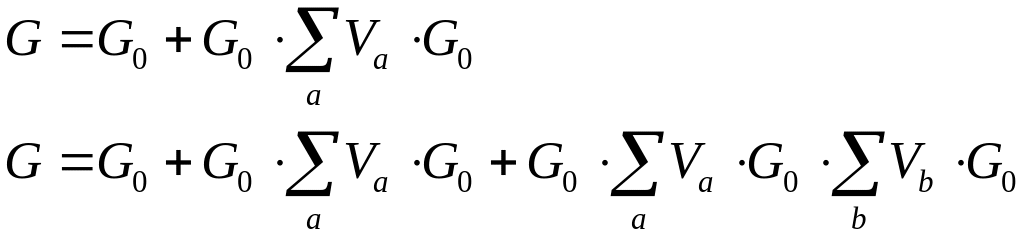
Второе слагаемое во второй итерации

Диаграммы

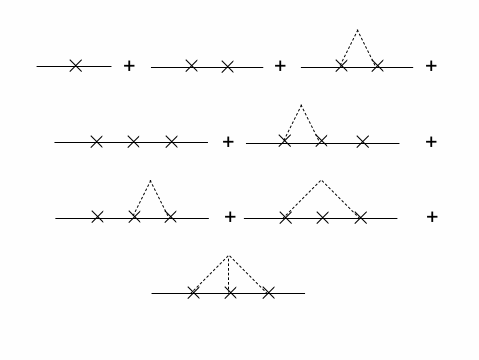
Сильно и слабо связанные диаграммы

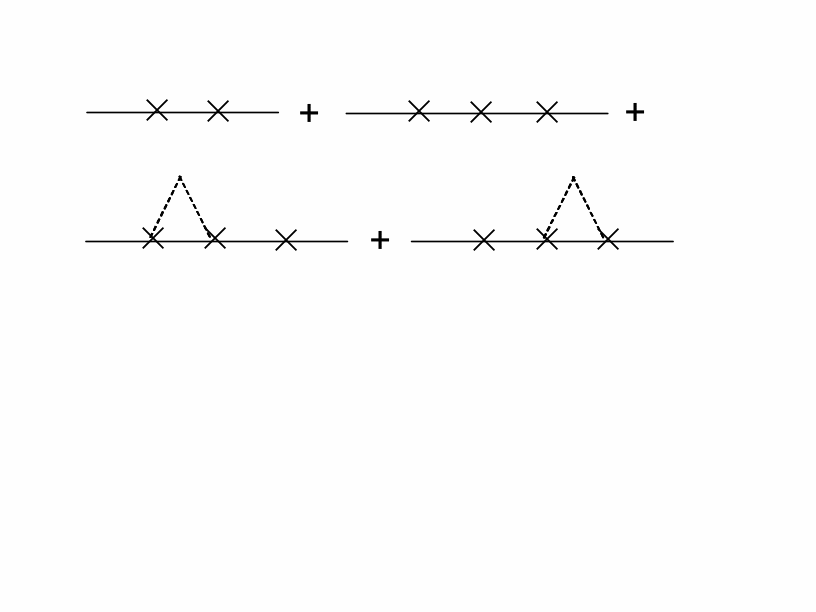
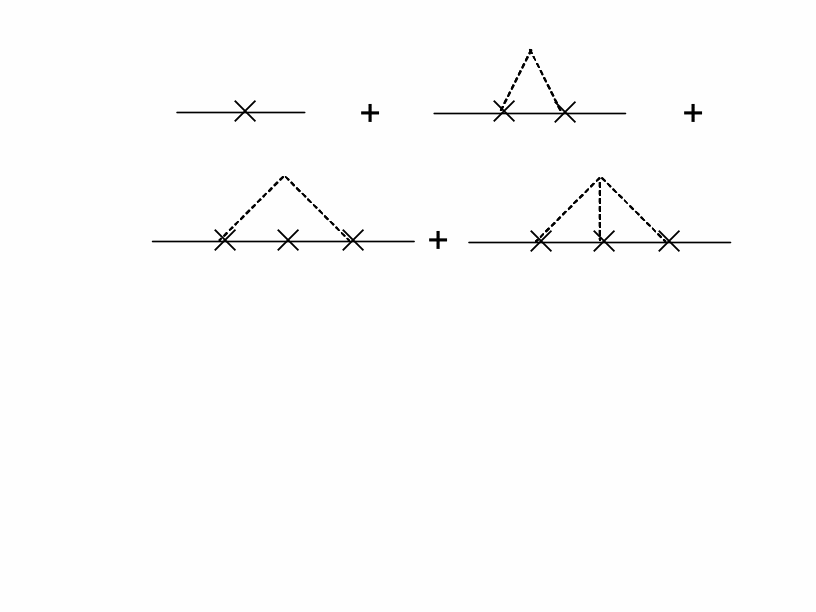
Графическое уравнение Фолди (Дайсона)

Массовый оператор

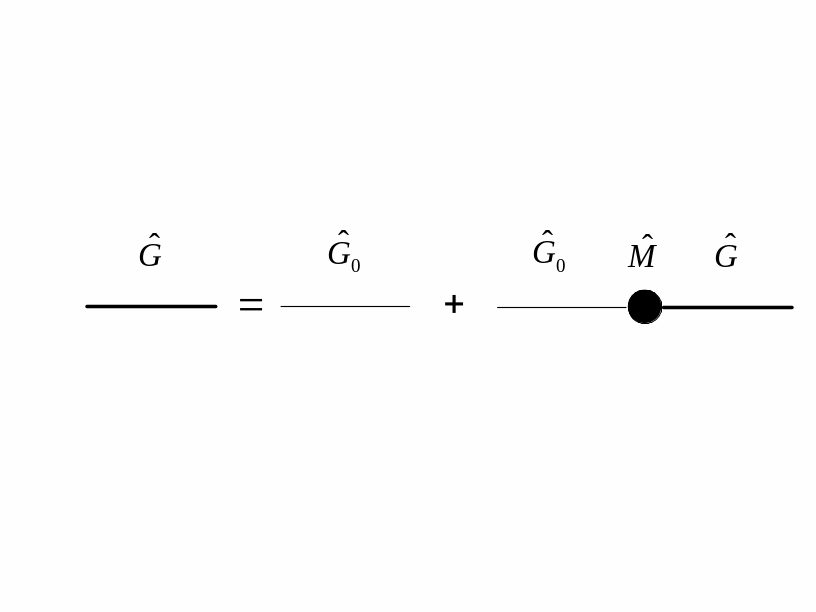
Уравнение Фолди (Дайсона) в явном виде

Приближение слабой локализации

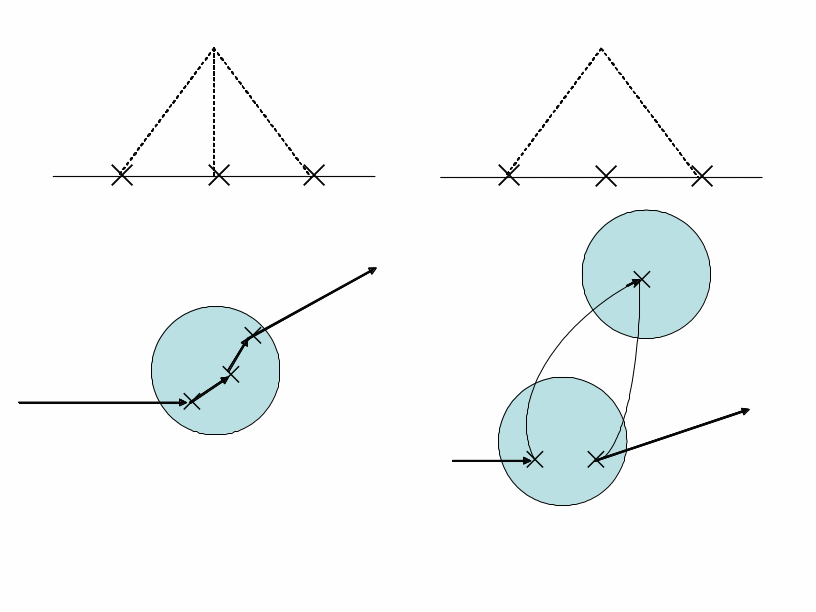
Массовый оператор в приближении слабой локализации

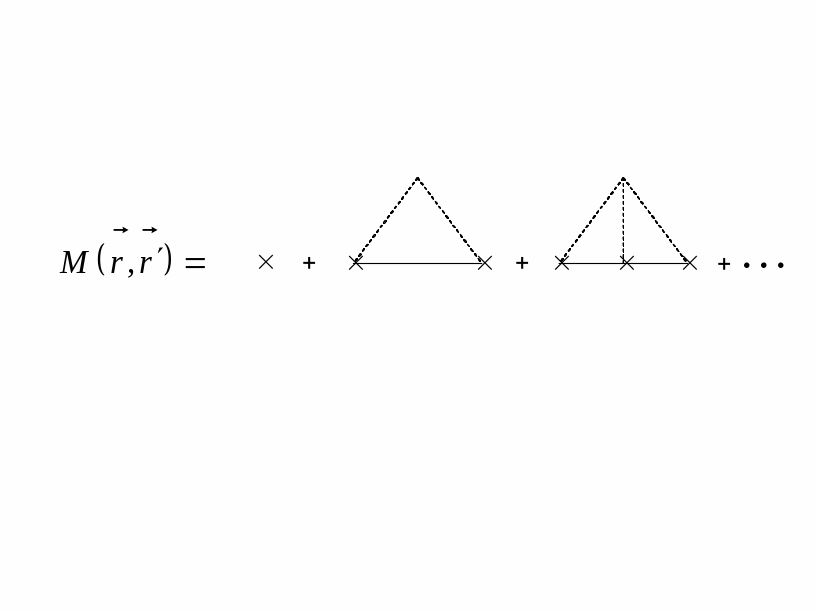
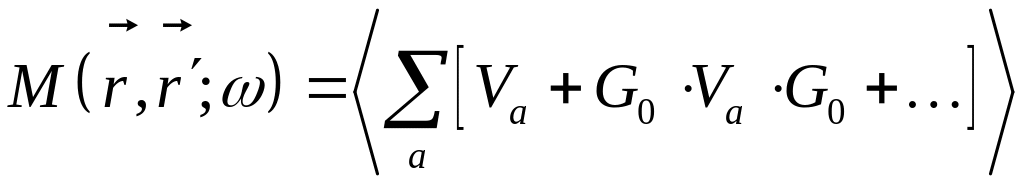
Матрица однократного рассеяния

В координатном представлении

Уравнение Тверского

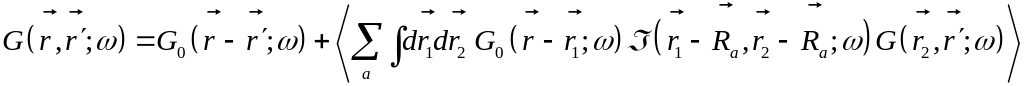
После усреднения в предположении некоррелированности рассеивателей

Приближение дальней зоны в уравнении Тверского

Первая итерация

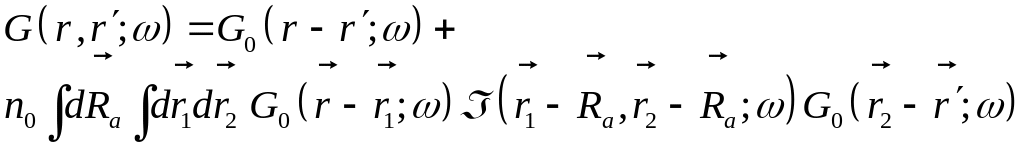
Характерный масштаб изменения матрицы рассеяния по аргументам ?

Замена переменных в первой итерации

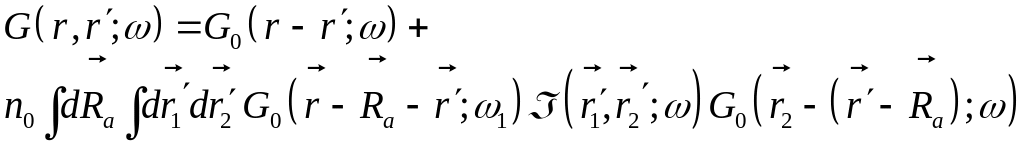
Представление свободной функции Грина в дальней зоне

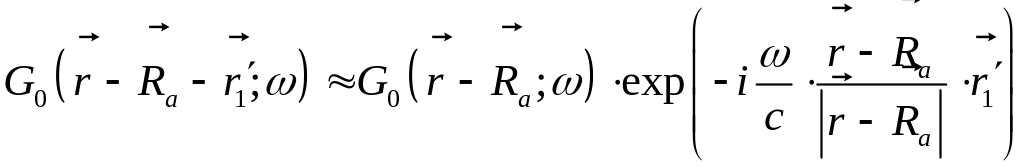
Матрица рассеяния в представлении волновых векторов

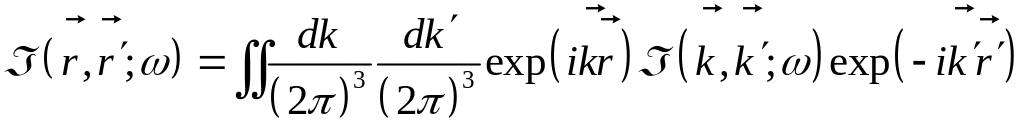
После итерационной процедуры находим

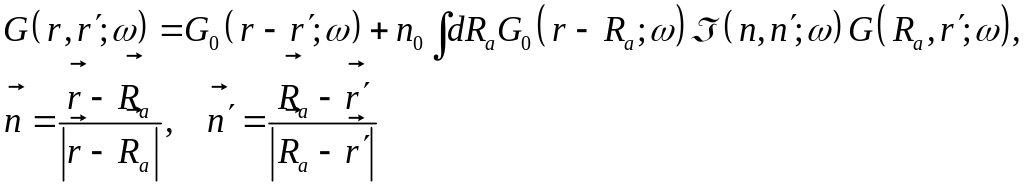
Бесконечная среда

Первая итерация

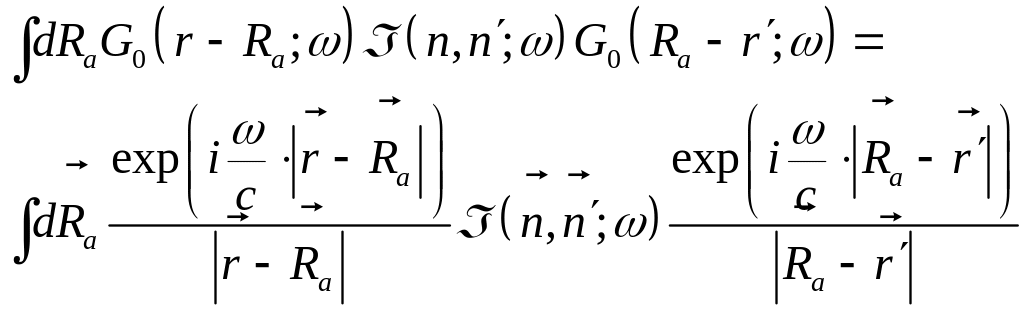
Метод стационарной фазы

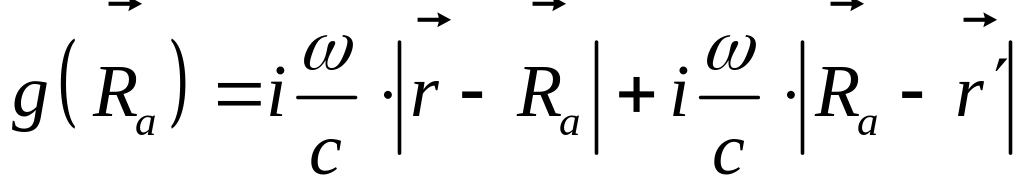
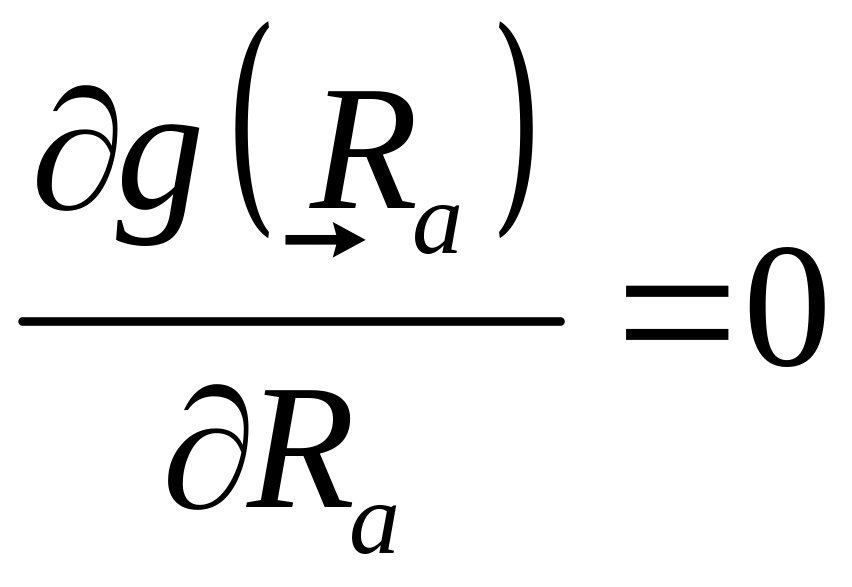
Условие применимости метода стационарной фазы

Условие скомпенсированности фаз

, где

Условие «плавности» поведения амплитуды

Или (условие дальней зоны или зоны Фраунгофера)

Интегральное уравнение для средней функции Грина

- амплитуда рассеяния «прямо-вперёд»

Дифференциальное уравнение для средней функции Грина

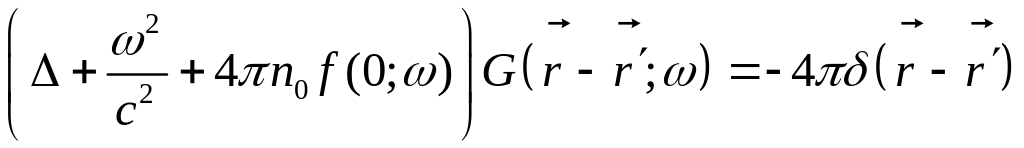
Решение для бесконечной среды

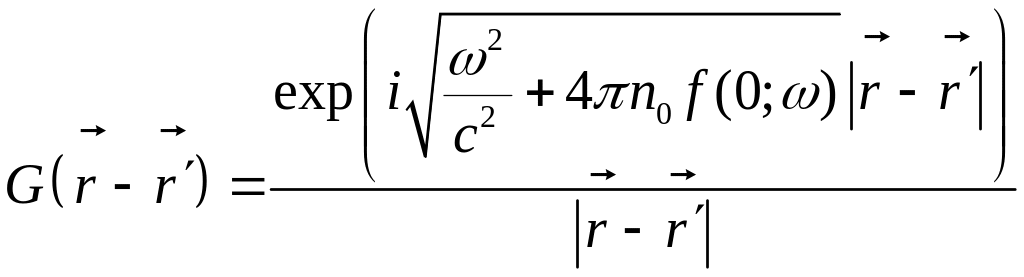
Оптическая теорема

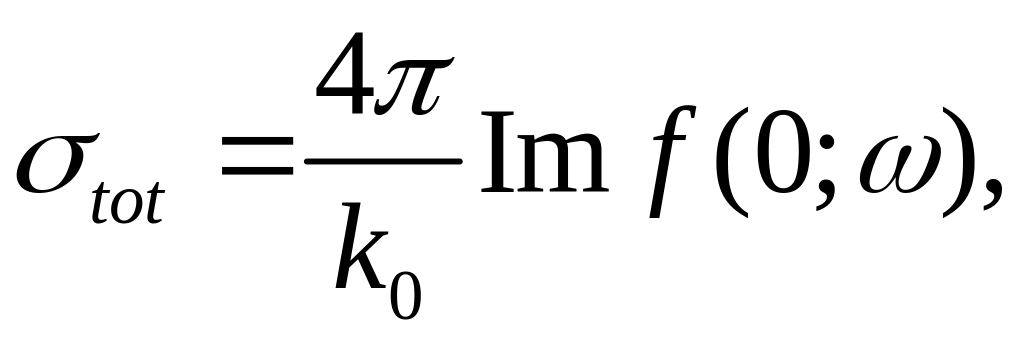
Длина ослабления

В отсутствие поглощения

В приближении слабой локализации

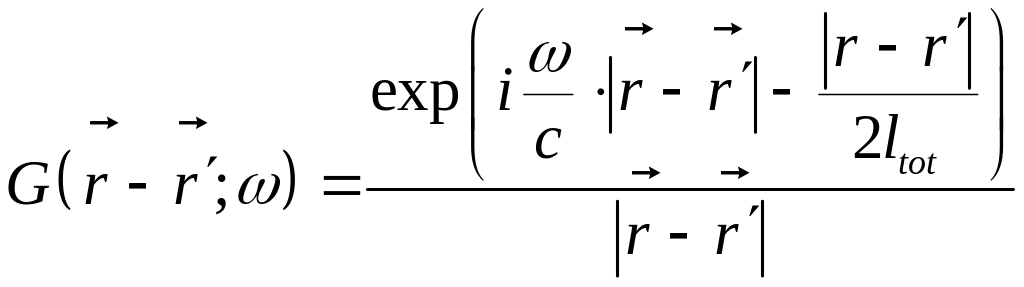
Вычислить

Рассеиватели нерезонансные – ширина резонанса ,

Поэтому

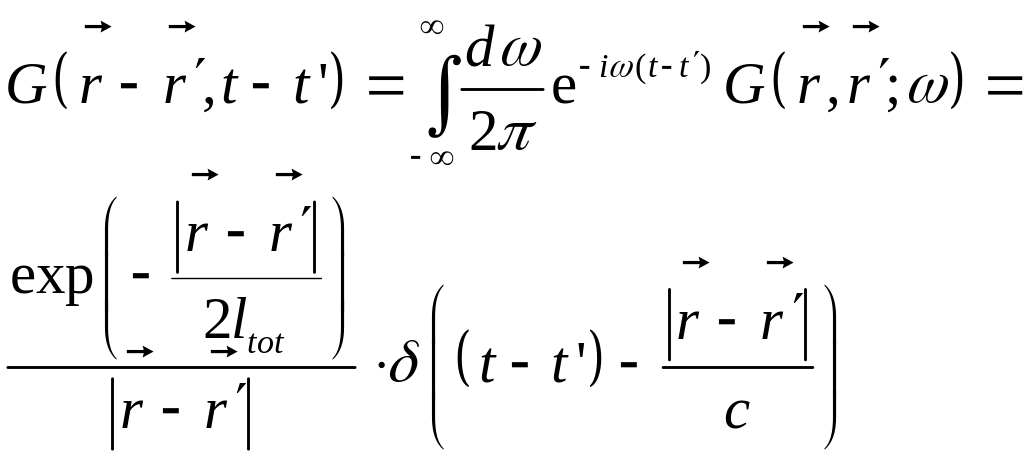
Волновое уравнение для средней функции Грина в пространственно-временном представлении

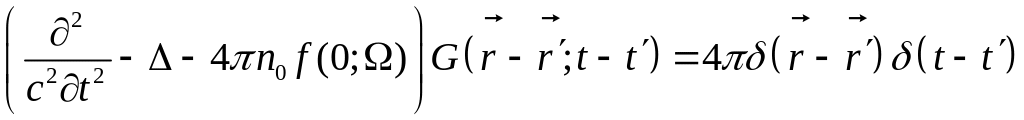
Уравнение для матрицы плотности нерассеянного поля в представлении Вигнера

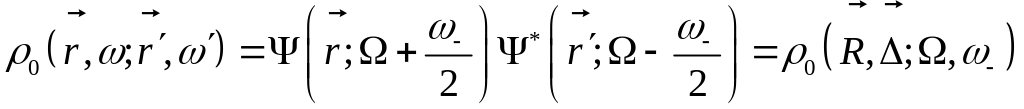
Вводим операторы

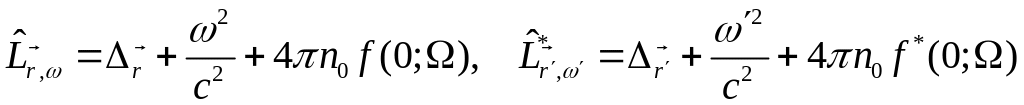
Перейти в уравнении

к представлению Вигнера, т.е. получить уравнение для

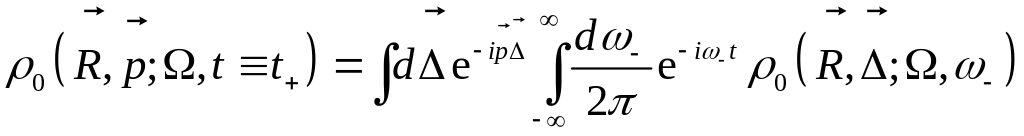
Промежуточное уравнение

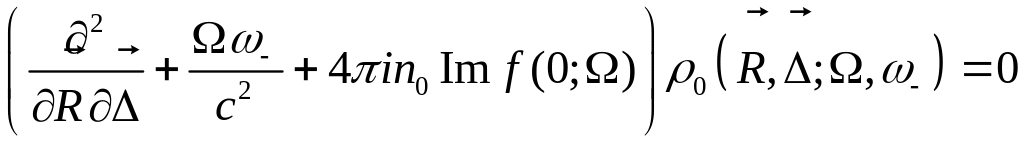
Здесь надо учесть оптическую теорему.

Ещё промежуточное уравнение

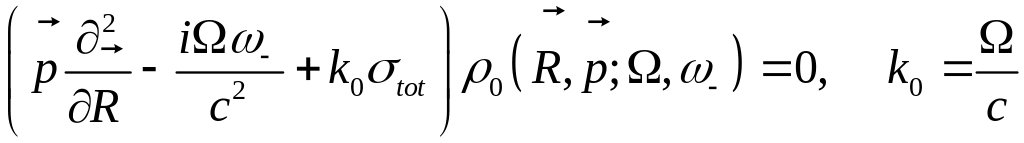
Окончательный результат

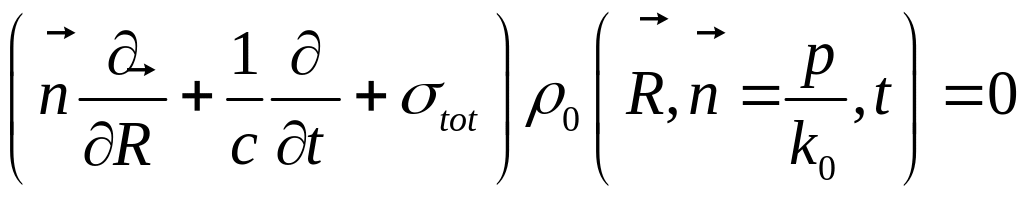
Функция Грина «укороченного» уравнения переноса

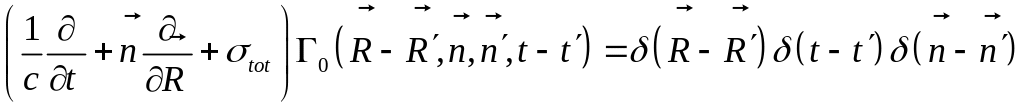
Преобразование Фурье по времени

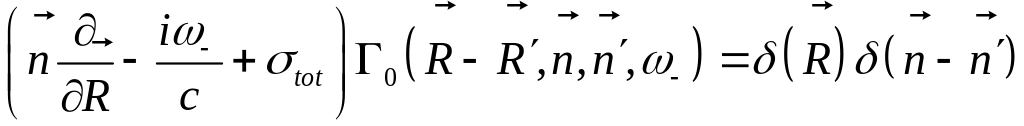
Ищем решение в виде

Уравнение для

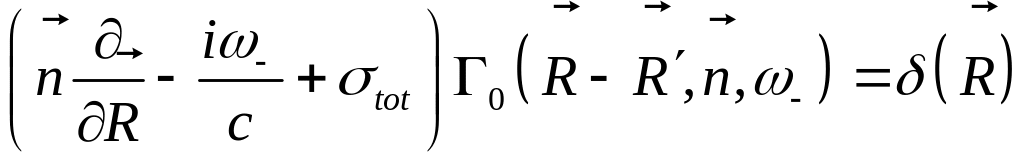
Решение